发展背景和原理
差分进化算法(Differential Evolution, DE)是一种基于群体的随机优化算法,由Storn和Price于1995年提出。该算法起源于遗传算法(Genetic Algorithm, GA),但其具有更简单的结构和更强的全局搜索能力。差分进化算法主要用于解决全局优化问题,通过变异、交叉和选择操作不断改进解的质量。
数学原理
差分进化算法的基本操作包括变异、交叉和选择。具体步骤如下:
-
初始化:初始化一个包含个个体的种群,每个个体是维向量,初始种群通常随机生成。
-
变异:对于每个个体,从种群中随机选择三个不同的个体,生成变异向量:
其中,是变异因子,通常取值在之间。
-
交叉:将变异向量与当前个体进行交叉,生成试验向量。交叉操作采用均匀交叉方式:
其中,是均匀分布的随机数,是交叉概率,是随机选择的一个维度。
-
选择:对于每个试验向量,与当前个体比较其适应度,如果试验向量的适应度更优,则选择试验向量进入下一代:
-
迭代:重复变异、交叉和选择操作,直到满足停止条件(如达到最大迭代次数或适应度不再显著提升)。
应用场景
差分进化算法具有全局优化能力强、实现简单等优点,广泛应用于以下场景:
-
参数优化:机器学习模型参数调优、神经网络权重优化等。
-
函数优化:非线性、多峰、多维函数的全局优化。
-
工程设计:结构优化、电力系统优化、化学过程优化等。
可视化Python示例
以下是使用差分进化算法优化Rosenbrock函数的Python示例,并进行可视化:
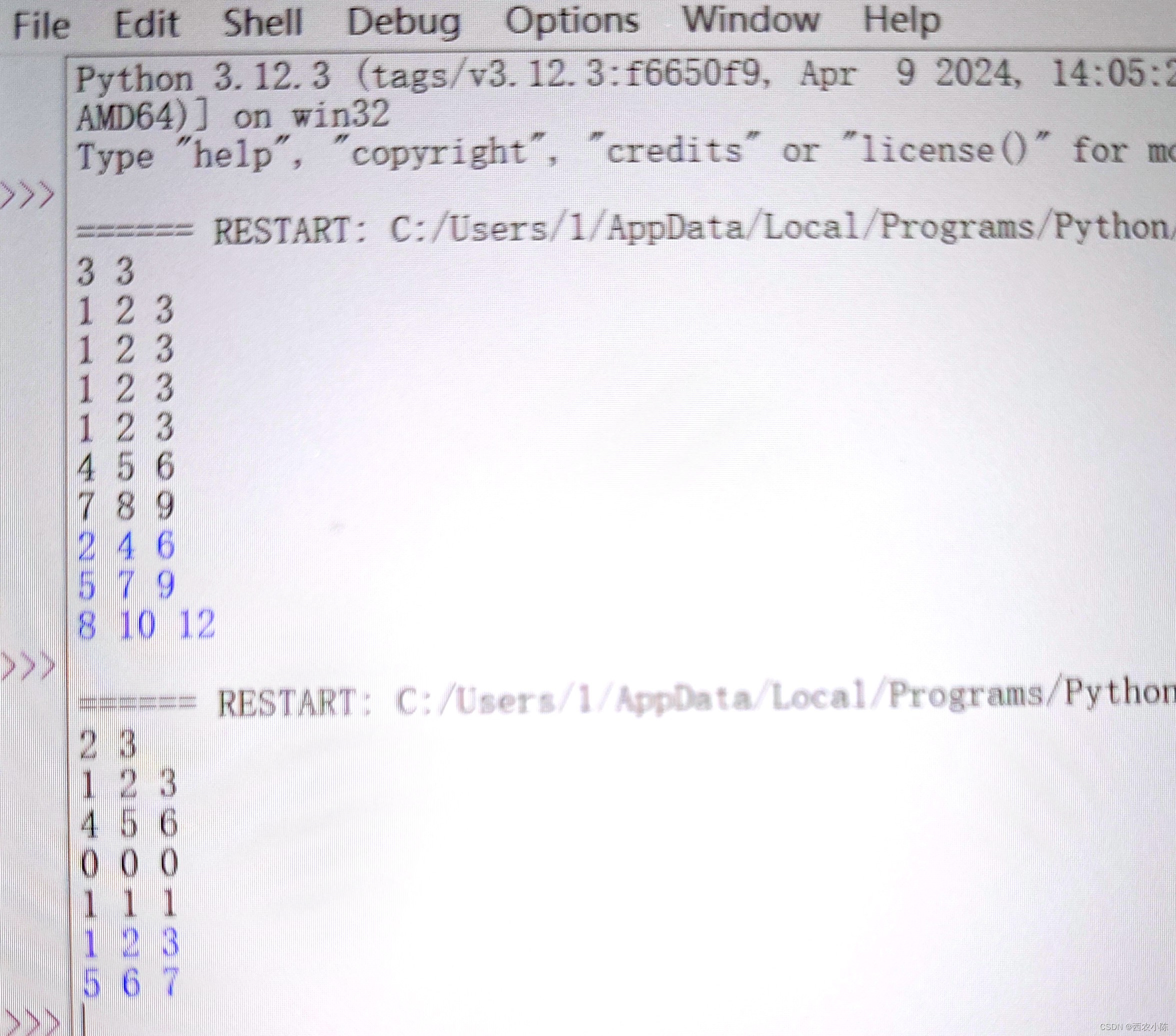
import numpy as np # 导入NumPy库,用于数值计算
import matplotlib.pyplot as plt # 导入Matplotlib库,用于绘图
from mpl_toolkits.mplot3d import Axes3D # 导入3D绘图工具
# 目标函数:Rosenbrock函数
def rosenbrock(x, y):
return 100.0 * (y - x**2.0)**2.0 + (1 - x)**2.0 # 计算Rosenbrock函数的值
# 创建网格数据
x = np.linspace(-2, 2, 400) # 在-2到2之间生成400个点
y = np.linspace(-1, 3, 400) # 在-1到3之间生成400个点
X, Y = np.meshgrid(x, y) # 创建网格数据
Z = rosenbrock(X, Y) # 计算网格数据对应的Rosenbrock函数值
plt.switch_backend('Qt5Agg') # 切换到Qt5Agg后端以在独立窗口中显示图形
# 创建独立窗口进行三维可视化
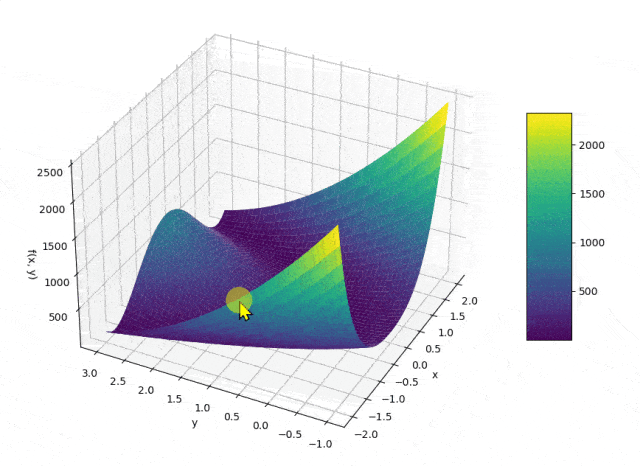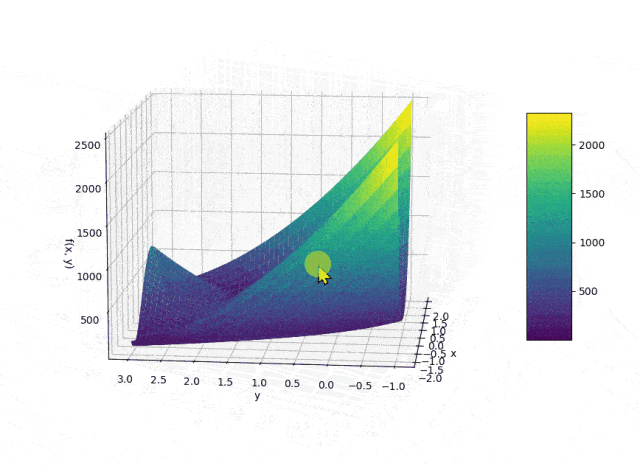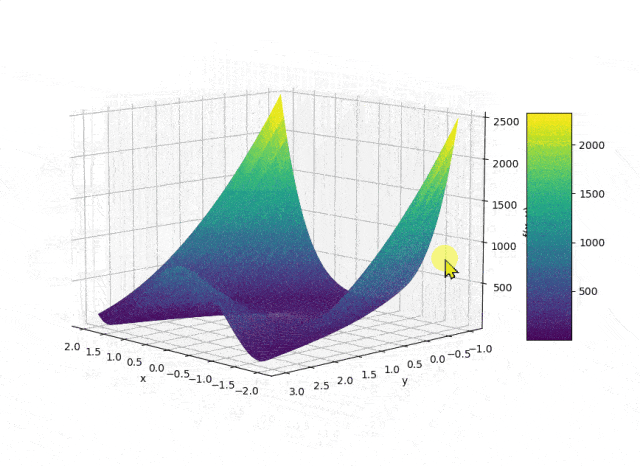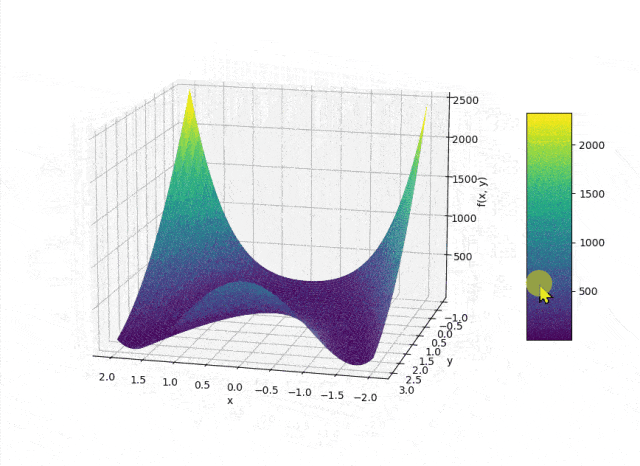
def visualize_rosenbrock_3d():
fig = plt.figure(figsize=(10, 8)) # 创建一个10x8英寸的图形
ax = fig.add_subplot(111, projection='3d') # 添加一个3D子图
# 绘制三维曲面
surf = ax.plot_surface(X, Y, Z, cmap='viridis', edgecolor='none') # 绘制Rosenbrock函数的三维曲面,使用Viridis配色方案,去除边缘颜色
# 添加颜色条
fig.colorbar(surf, shrink=0.5, aspect=5) # 添加颜色条,设置收缩比例和宽高比
# 添加坐标轴标签和标题
ax.set_xlabel('x') # 设置x轴标签
ax.set_ylabel('y') # 设置y轴标签
ax.set_zlabel('f(x, y)') # 设置z轴标签
ax.set_title('3D Visualization of Rosenbrock Function') # 设置图形标题
# 显示图形窗口
plt.show() # 显示图形
# 目标函数:Rosenbrock函数(差分进化使用)
def rosenbrock_diff(x):
x = np.array(x) # 将输入转换为NumPy数组
return sum(100.0 * (x[1:] - x[:-1]**2.0)**2.0 + (1 - x[:-1])**2.0) # 计算Rosenbrock函数值的总和
# 差分进化算法
def differential_evolution(objective, bounds, n_iter, n_pop, F, CR):
# 初始化种群
pop = bounds[:, 0] + (bounds[:, 1] - bounds[:, 0]) * np.random.rand(n_pop, len(bounds)) # 生成初始种群
best_idx = np.argmin([objective(ind) for ind in pop]) # 找到种群中最好的个体索引
best = pop[best_idx] # 最好的个体
best_score = objective(best) # 最好的个体的得分
scores = [best_score] # 保存每代最好的得分
for gen in range(n_iter): # 遍历每一代
for i in range(n_pop): # 遍历种群中的每一个个体
idxs = [idx for idx in range(n_pop) if idx != i] # 获取其他个体的索引
a, b, c = pop[np.random.choice(idxs, 3, replace=False)] # 随机选择三个不同的个体
mutant = np.clip(a + F * (b - c), bounds[:, 0], bounds[:, 1]) # 生成变异个体,并确保其在边界内
cross_points = np.random.rand(len(bounds)) < CR # 生成交叉点
if not np.any(cross_points): # 确保至少有一个交叉点
cross_points[np.random.randint(0, len(bounds))] = True
trial = np.where(cross_points, mutant, pop[i]) # 生成试验个体
f_trial = objective(trial) # 计算试验个体的得分
if f_trial < objective(pop[i]): # 如果试验个体比当前个体好
pop[i] = trial # 替换当前个体
if f_trial < best_score: # 如果试验个体比最好的个体还好
best, best_score = trial, f_trial # 更新最好的个体和得分
scores.append(best_score) # 保存最好的得分
print(f"Generation {gen+1}, Best Score: {best_score}") # 打印当前代和最好的得分
return best, best_score, scores # 返回最好的个体,最好的得分和每代的最好的得分
# 参数设置
bounds = np.asarray([[-5.0, 5.0], [-5.0, 5.0]]) # 设置搜索空间边界
n_iter = 100 # 设置迭代次数
n_pop = 50 # 设置种群大小
F = 0.8 # 设置变异因子
CR = 0.7 # 设置交叉概率
# 运行差分进化算法
best, score, scores = differential_evolution(rosenbrock_diff, bounds, n_iter, n_pop, F, CR) # 调用差分进化算法
print(f"Best Solution: {best}, Best Score: {score}") # 打印最好的解和最好的得分
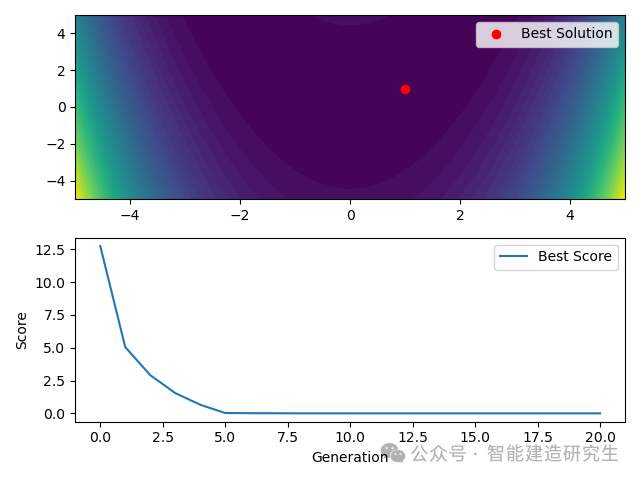
# 差分进化算法的二维可视化
plt.figure() # 创建一个新图形
plt.subplot(2, 1, 1) # 创建第一个子图
x = np.linspace(bounds[0, 0], bounds[0, 1], 100) # 生成x轴数据
y = np.linspace(bounds[1, 0], bounds[1, 1], 100) # 生成y轴数据
X, Y = np.meshgrid(x, y) # 创建网格数据
Z = np.array([rosenbrock_diff([x, y]) for x, y in zip(np.ravel(X), np.ravel(Y))]).reshape(X.shape) # 计算每个网格点的Rosenbrock函数值
plt.contourf(X, Y, Z, levels=50, cmap='viridis') # 绘制等高线图
plt.plot(best[0], best[1], 'ro', label='Best Solution') # 绘制最好的解
plt.legend() # 显示图例
plt.subplot(2, 1, 2) # 创建第二个子图
plt.plot(scores, label='Best Score') # 绘制每代最好的得分
plt.xlabel('Generation') # 设置x轴标签
plt.ylabel('Score') # 设置y轴标签
plt.legend() # 显示图例
plt.tight_layout() # 调整子图布局
plt.show() # 显示图形
# 三维可视化Rosenbrock函数
visualize_rosenbrock_3d() # 调用三维可视化函数
以上内容总结自网络,如有帮助欢迎转发,我们下次再见!