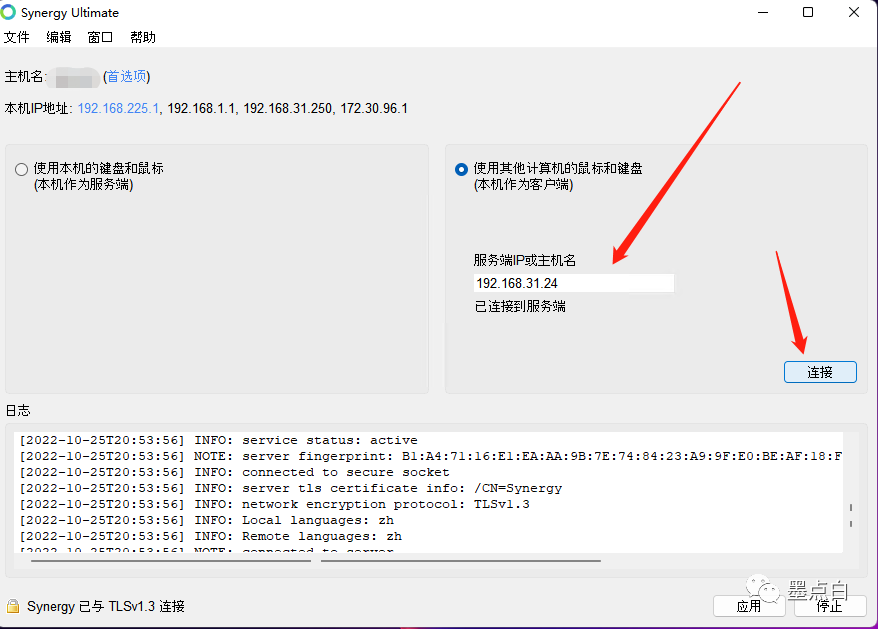
测试效果


简介
MLS(Moving Least Squares,移动最小二乘法)算法在法线估计中的应用是一种基于局部数据拟合的技术,它通过对点云中每个点的邻域数据进行多项式拟合来估计该点的法线。以下是MLS算法在法线估计中的详细解释:
MLS算法的基本原理
MLS算法是一种无网格的曲线和曲面拟合技术,它通过为每个点定义一个局部邻域,并在该邻域内使用最小二乘法拟合一个多项式函数来逼近曲面。这个多项式函数可以是平面的(一阶)或者更复杂的曲面(如二阶或更高阶)。通过拟合得到的多项式函数,可以进一步计算该点的法线向量。
MLS算法在法线估计中的应用
- 定义邻域:
-
- 对于点云中的每个点,首先定义其邻域范围。这可以通过固定半径(如0.03米)或固定数量的最近邻居点来实现。
- 多项式拟合:
-
- 在每个点的邻域内,使用多项式函数来逼近这些点。多项式函数的阶数可以根据实际需求进行选择,通常一阶或二阶多项式就足以满足大多数需求。
- 通过最小二乘法优化多项式函数的系数,使得多项式函数在