信息学奥赛初赛天天练-46-CSP-J2020阅读程序2-进制转换、十进制转k进制、等比数列通项公式、等比数列求和公式应用

news2024/9/24 15:27:55

PDF文档公众号回复关键字:20240713

在这里插入图片描述

2020 CSP-J 阅读程序2

1阅读程序(程序输入不超过数组或字符串定义的范围；判断题正确填 √，错误填 ×。除特殊说明外，判断题 1.5 分，选择题 3 分，共计 40 分)

01 #include <iostream>
02 using namespace std;
03 
04 long long n, ans;
05 int k, len;
06 long long d[1000000];
07 
08 int main() {
09   cin >> n >> k;
10   d[0] = 0;
11   len= 1;
12   ans = 0;
13   for (long long i = 0; i <n; ++i) {
14     ++d[0];
15     for (int j = 0; j + 1<len; ++j) {
16       if (d[j] == k) {
17         d[j] = 0;
18         d[j + 1] += 1;
19         ++ans;
20       }
21     }
22     if (d[len- 1] == k) {
23       d[len - 1] = 0;
24       d[len] =1;
25       ++len;
26       ++ans;
27     }
28   }
29   cout << ans << endl;
30   return 0;
31 }

假设输入的 n 是不超过 2^62 的正整数，k都是不超过 10000 的正整数，完成下面的判断题和单选题

判断题

22.若 k=1，则输出 ans 时，len=n ( ) [1.5分]

23.若 k>1，则输出 ans 时，len —定小于 n ( ) [1.5分]

24.若 k>1，则输出 ans 时，klen —定大于n ( ) [1.5分]

单选题

25.若输入的n等于：10^15，输入的 k 为 1，则输出等于( )[3分]

A.1

B.(10^30 − 10^15)/2

C.(10^30 + 10^15)/2

D.10^15

26.若输入的 n 等于205,891,132,094,649（即330），输入的 k 为 3，则输出等于( )[3分]

A.3^30

B.(3^30−1)/2

C.3^30−1

D.(3^30+1)/2

27.若输入的 n 等于 100,010,002,000,090，输入的 k 为 10，则输出等于( )[3分]

A.11,112,222,444,543

B.11,122,222,444,453

C.11,122,222,444,543

D.11,112,222,444,453

2 相关知识点

1)十进制整数转R进制

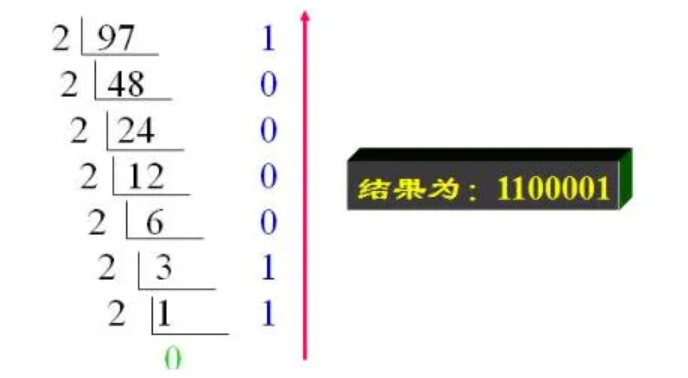
2) 十进制小数转R进制

2) 等比数列

等比数列通项公式

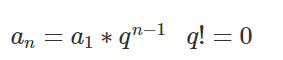
n项等比数列，其中 a1是首项，an是第n项，q为公比

例如

a1=1，q=2

a3=1*2^(3-1)=4

等比数列求和公式

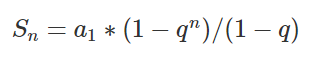
Sn为n项等比数列，首项为a1，公比为q的和

例如

a1=1，q=2

S3=1*(1-2^3)/(1-2)=7

3 思路分析

/*
  ans每次进位都会加1，因此ans表示总的进位次数
  len在len-1需要进位时才加1，并且进位，因此len是所有数字的长度
*/
11   len= 1;
12   ans = 0;

/*
  从如下代码可以看出d[0]一直累加 判断是否到k，到k后清0
  把n拆分成多个k，满足k后进位
*/
10   d[0] = 0;
14     ++d[0];
16       if (d[j] == k) {
17         d[j] = 0;
22     if (d[len- 1] == k) {
23       d[len - 1] = 0;

/*
  当前长度0~len-1，逐位判断是否达到k，达到k后进位
*/
15     for (int j = 0; j + 1<len; ++j) {
16       if (d[j] == k) {
17         d[j] = 0;
18         d[j + 1] += 1;
19         ++ans;
20       }
21     }
/*
  判断最后一位是否达到k，达到k后进位，增加长度
*/
22     if (d[len- 1] == k) {
23       d[len - 1] = 0;
24       d[len] =1;
25       ++len;
26       ++ans;
27     }

假设输入的 n 是不超过 2^62 的正整数，k都是不超过 10000 的正整数，完成下面的判断题和单选题

判断题

22.若 k=1，则输出 ans 时，len=n ( F ) [1.5分]

分析

k=1时，打破了进位逻辑，len最大为2
例如 n=3 k=1 时，len=2 n=3 不相等，具体如下
i=0时，执行22行，d[0]=0,d[1]=1,len=2,ans=1
i=1时，执行15行，d[0]=0,d[1]=2,len=2,ans=2，不满足22行
i=2时，执行15行，d[0]=0,d[1]=3,len=2,ans=3，不满足22行

23.若 k>1，则输出 ans 时，len —定小于 n ( F ) [1.5分]

分析

len是k进制的位数，当n=2，k=2时，len=2，n=2 即 len=n
所以错误

24.若 k>1，则输出 ans 时，k^len —定大于n ( T ) [1.5分]

分析

n用k进制表示，最大值为k^len-1
k^len>k^len-1
所以k^len>n

例如 n=3，k=2时 len为2
k^len=2^2=4
n=3
k^len>n