- 数字电路的分类:组合逻辑电路,时序逻辑电路。
- 本章学习组合逻辑电路。
4.1 组合逻辑电路的分析
- 给定的逻辑电路,确定其逻辑表达式,列出真值表,得到简化后的逻辑表达式,分析得到其功能。
3位奇校验电路
(1) 如下图所示。
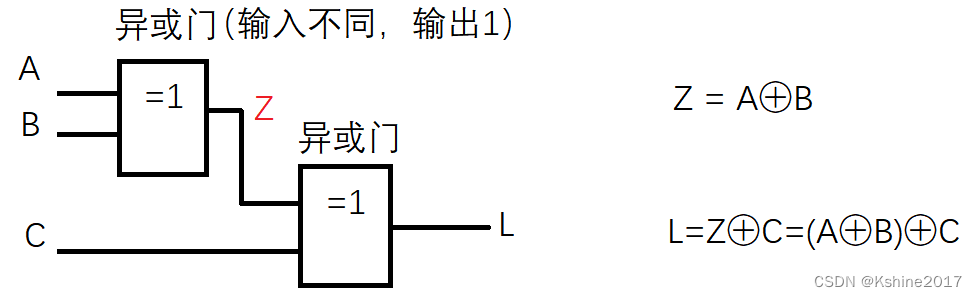
(2)列出真值表
| A | B | C | Z | L |
|---|---|---|---|---|
| 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 1 | 0 | 1 |
| 0 | 1 | 0 | 1 | 1 |
| 0 | 1 | 1 | 1 | 0 |
| 1 | 0 | 0 | 1 | 1 |
| 1 | 0 | 1 | 1 | 0 |
| 1 | 1 | 0 | 0 | 0 |
| 1 | 1 | 1 | 0 | 1 |
(3) 分析出奇校验电路功能。
- 当C为1时,且AB中有0个或2个1时(AB同,Z=0),(奇数个1),L为1。
- 当C为0时,且AB中只有1个1时(AB异,Z=1),(奇数个1),L为1。
- 即,ABC中出现奇数个1时,L为1。ABC中出现偶数个1时,L为0。
3位偶校验电路
(1)在奇校验电路的基础上,在输出端再加一级反相器,可以得到偶校验电路。
3位取反码电路
- 如下图所示。
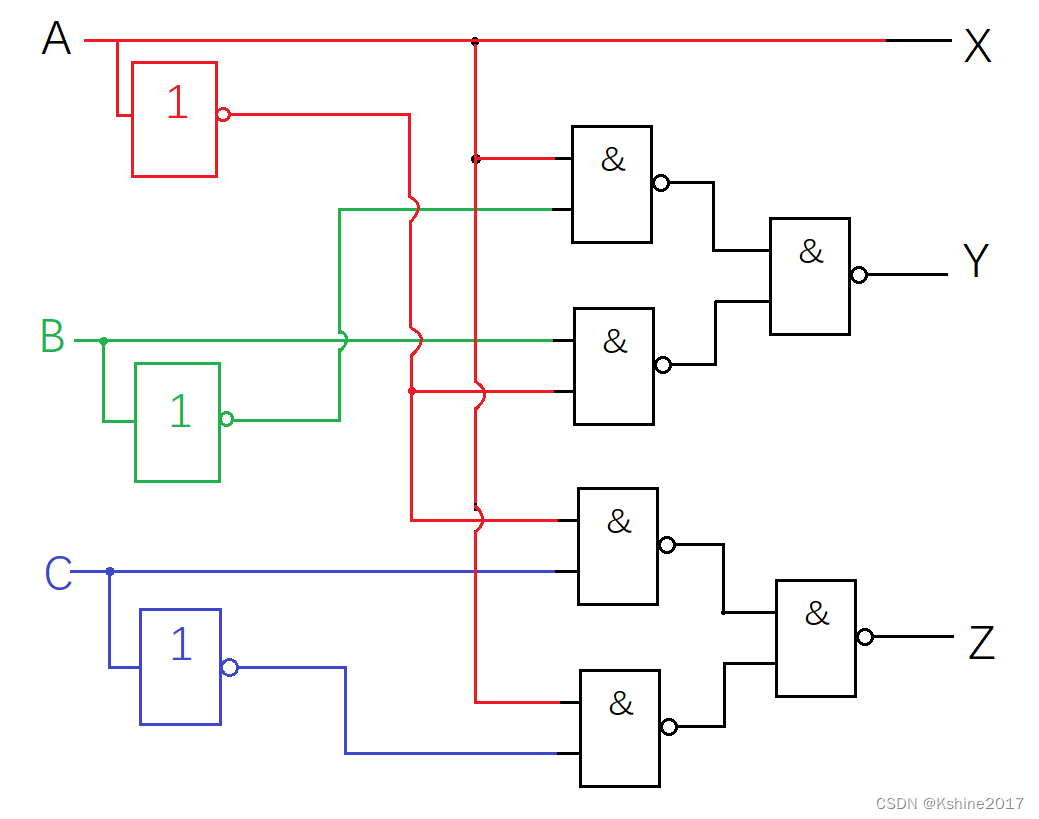
- 逻辑表达式。
X = A X = A X=A
Y = ( A ⋅ B ‾ ‾ ) ⋅ ( A ‾ ⋅ B ) ‾ ‾ = A ⋅ B ‾ + A ‾ ⋅ B Y = \overline{(\overline{A·\overline{B}})·(\overline{\overline{A}·B)}}=A·\overline{B}+\overline{A}·B Y=(A⋅B)⋅(A⋅B)=A⋅B+A⋅B
Z = ( A ‾ ⋅ C ‾ ) ⋅ ( A ⋅ C ‾ ) ‾ ‾ = A ‾ ⋅ C + A ⋅ C ‾ Z=\overline{(\overline{\overline{A}·C})·(\overline{A·\overline{C})}}=\overline{A}·C+A·\overline{C} Z=(A⋅C)⋅(A⋅C)=A⋅C+A⋅C - 真值表。
| A | B | C | X | Y | Z |
|---|---|---|---|---|---|
| 0 | 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 1 | 0 | 0 | 1 |
| 0 | 1 | 0 | 0 | 1 | 0 |
| 0 | 1 | 1 | 0 | 1 | 1 |
| 1 | 0 | 0 | 1 | 1 | 1 |
| 1 | 0 | 1 | 1 | 1 | 0 |
| 1 | 1 | 0 | 1 | 0 | 1 |
| 1 | 1 | 1 | 1 | 0 | 0 |
- 功能分析。
(1)原码ABC,A作为符号位,0表示正数,1表示负数。
(2)反码XYZ,X作为符号位,与A一致。
(3)当A=0正数时,YZ和BC一致。
(4)当A=1负数时,符号位不变X=A,YZ为BC取反后的结果。
4.2 组合逻辑电路设计
- 明确逻辑功能,确定输入输出,列出真值表,写出逻辑表达式,简化变换逻辑表达式,画出逻辑图。
3位火车进站指示灯
-
需求。
(1)使用2输入与非门,反相器。
(2)1号指示灯,特快车进站指示灯。优先级高。
(3)2号指示灯,直快车进站指示灯。优先级中。
(4)3号指示灯,慢车进站指示灯。优先级低。
(5)同时最多只能有一个指示灯亮。 -
定义输入输出变量。
(1)输入信号, I 0 特快请求, I 1 直快请求, I 2 慢车请求 I_0特快请求,I_1直快请求,I_2慢车请求 I0特快请求,I1直快请求,I2慢车请求。1表示有进站请求,0表示无进站请求。
(2)输出信号, L 0 特快进站指示灯, L 1 直快进站指示灯, L 2 慢车进站指示灯 L_0特快进站指示灯,L_1直快进站指示灯,L_2慢车进站指示灯 L0特快进站指示灯,L1直快进站指示灯,L2慢车进站指示灯。1表示灯亮,0表示灯不亮。 -
真值表。
| 输入 | 输出 | ||||
| I_0 | I_1 | I_2 | L_0 | L_1 | L_2 |
| 0 | 0 | 0 | 0 | 0 | 0 |
| 1 | X | X | 1 | 0 | 0 |
| 0 | 1 | X | 0 | 1 | 0 |
| 0 | 0 | 1 | 0 | 0 | 1 |
-
列出逻辑表达式
L 0 = I 0 L_0 = I_0 L0=I0
L 1 = I 0 ‾ ⋅ I 1 L_1 = \overline{I_0}·I_1 L1=I0⋅I1
L 2 = I 0 ‾ ⋅ I 1 ‾ ⋅ I 2 L_2 = \overline{I_0}·\overline{I_1}·I_2 L2=I0⋅I1⋅I2 -
根据需求,变换为与非形式。
L 0 = I 0 L_0 = I_0 L0=I0
L 1 = I 0 ‾ ⋅ I 1 ‾ ‾ L_1 = \overline{\overline{\overline{I_0}·I_1}} L1=I0⋅I1
L 2 = I 0 ‾ ⋅ I 1 ‾ ‾ ‾ ⋅ I 2 ‾ ‾ L_2 =\overline{\overline{\overline{\overline{\overline{I_0}·\overline{I_1}}}·I_2}} L2=I0⋅I1⋅I2 -
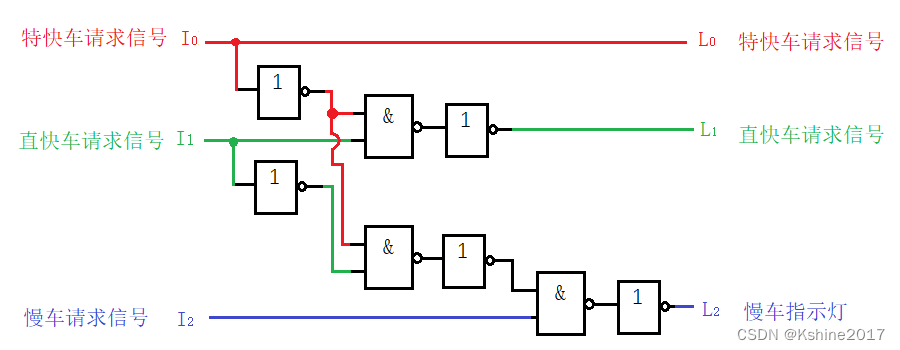
画出逻辑图。
(1)一片74HC00芯片,包含4个2输入CMOS与非门。
(2)一片74HC04芯片,包含6个CMOS反相器。
4位格雷码转自然二进制码
-
需求。
(1)可以使用任何逻辑门电路。
(2)4位格雷码,转换为自然二进制码。 -
定义输入输出变量。
(1)输入变量, G 3 , G 2 , G 1 , G 0 G_3,G_2,G_1,G_0 G3,G2,G1,G0。
(2)输出变量, B 3 , B 2 , B 1 , B 0 B_3,B_2,B_1,B_0 B3,B2,B1,B0。 -
列出真值表。
| 输入 | 输出 | ||||||
| G_3 | G_2 | G_1 | G_0 | B_3 | B_2 | B_1 | B_0 |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 0 | 1 | 0 | 0 | 0 | 1 |
| 0 | 0 | 1 | 1 | 0 | 0 | 1 | 0 |
| 0 | 0 | 1 | 0 | 0 | 0 | 1 | 1 |
| 0 | 1 | 1 | 0 | 0 | 1 | 0 | 0 |
| 0 | 1 | 1 | 1 | 0 | 1 | 0 | 1 |
| 0 | 1 | 0 | 1 | 0 | 1 | 1 | 0 |
| 0 | 1 | 0 | 0 | 0 | 1 | 1 | 1 |
| 1 | 1 | 0 | 0 | 1 | 0 | 0 | 0 |
| 1 | 1 | 0 | 1 | 1 | 0 | 0 | 1 |
| 1 | 1 | 1 | 1 | 1 | 0 | 1 | 0 |
| 1 | 1 | 1 | 0 | 1 | 0 | 1 | 1 |
| 1 | 0 | 1 | 0 | 1 | 1 | 0 | 0 |
| 1 | 0 | 1 | 1 | 1 | 1 | 0 | 1 |
| 1 | 0 | 0 | 1 | 1 | 1 | 1 | 0 |
| 1 | 0 | 0 | 0 | 1 | 1 | 1 | 1 |
-
根据真值表,画出卡诺图。
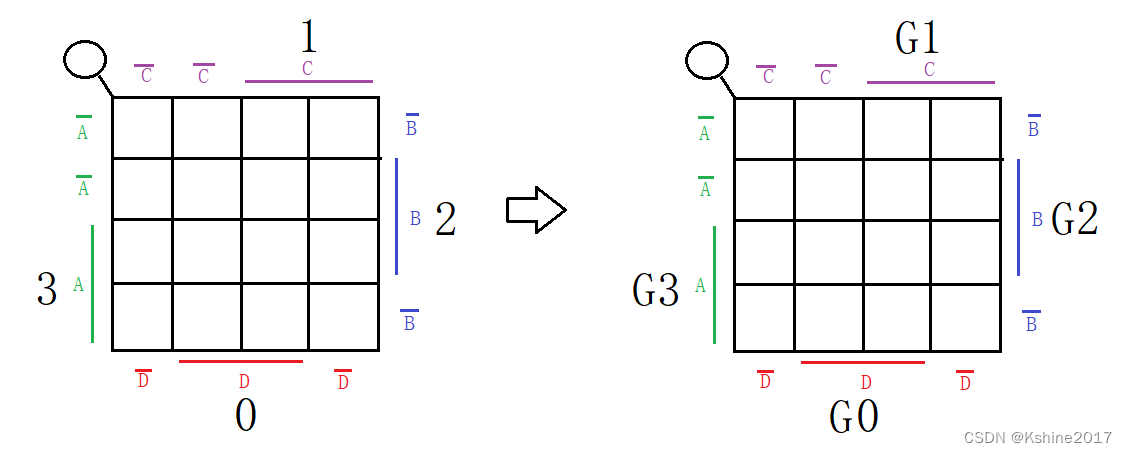
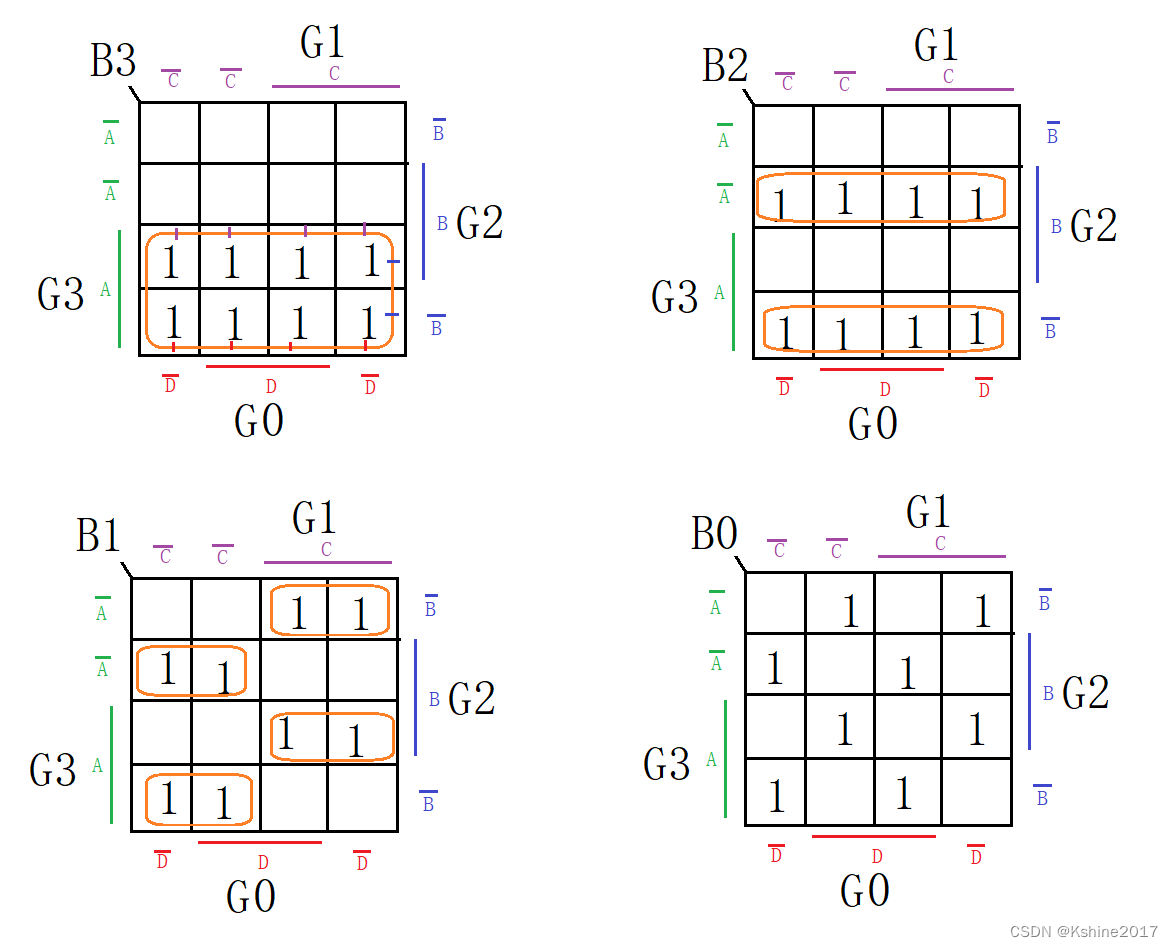
-
列出逻辑表达式。
B 3 = G 3 B_3 = G_3 B3=G3
B 2 = G 3 ‾ ⋅ G 2 + G 3 ⋅ G 2 ‾ = G 3 ⊕ G 2 B_2 = \overline{G_3}·G_2 + G_3·\overline{G_2}=G_3⊕G_2 B2=G3⋅G2+G3⋅G2=G3⊕G2
B 1 = G 3 ‾ G 2 G 1 ‾ + G 3 G 2 ‾ G 1 ‾ + G 3 ‾ G 2 ‾ G 1 + G 3 G 2 G 1 = ( G 3 G 2 ‾ + G 3 ‾ G 2 ) G 1 ‾ + ( G 3 G 2 ‾ + G 3 ‾ G 2 ) ‾ G 1 = G 3 ⊕ G 2 ⊕ G 1 B_1 = \overline{G_3}G_2\overline{G_1}+G_3\overline{G_2}\overline{G_1}+\overline{G_3}\overline{G_2}G_1+G_3G_2G_1=(G_3\overline{G_2}+\overline{G_3}G_2)\overline{G_1}+\overline{(G_3\overline{G_2}+\overline{G_3}G_2)}G_1=G_3⊕G_2⊕G_1 B1=G3G2G1+G3G2G1+G3G2G1+G3G2G1=(G3G2+G3G2)G1+(G3G2+G3G2)G1=G3⊕G2⊕G1
B 0 = G 3 ⊕ G 2 ⊕ G 1 ⊕ G 0 B_0=G_3⊕G_2⊕G_1⊕G_0 B0=G3⊕G2⊕G1⊕G0 -
画出逻辑图。
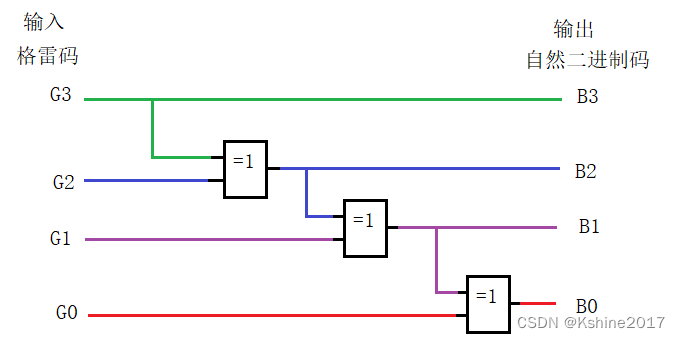
4.3 组合逻辑电路中的竞争与冒险
- 组合逻辑电路中,信号经过逻辑门都需要一定的时间。
- 信号经过不同的路径,传输时间不同(逻辑门的级数不同,逻辑门的种类不同)。
- 竞争:一个逻辑门的多个输入端的信号同时向相反方向变化,变化的时间有差异的现象,称为“竞争”。(谁先变化,谁后变化,即为竞争)。
- 冒险:竞争产生的输出干扰窄脉冲,这种现象称为冒险。
4.3.1 产生竞争冒险的原因
- 输入信号不能同时到达,导致出现短时间的异常窄脉冲。
- 与门
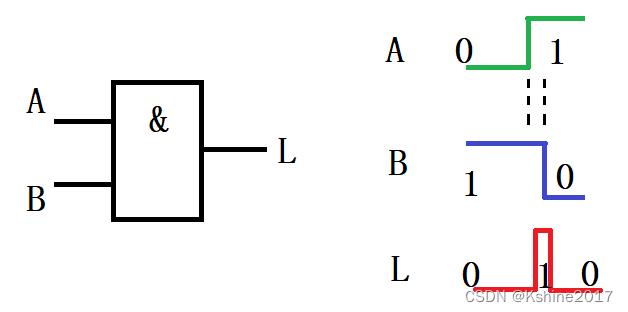
- 或门
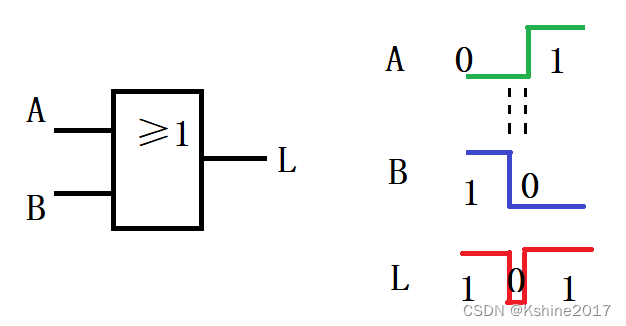
4.3.2 消去竞争冒险的方法
1. 发现并消去互补相乘项
- F = ( A + B ) ( A ‾ + C ) F = (A+B)(\overline{A}+C) F=(A+B)(A+C)
- 当B=C=0时,会出现 A A ‾ A\overline{A} AA乘积项。
- 发现:
A
A
‾
A\overline{A}
AA乘积项可能会导致“竞争冒险”。
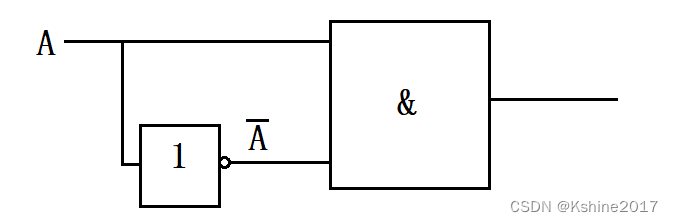
- 互补相乘项: A ⋅ A ‾ A·\overline{A} A⋅A。
- 消去: F = ( A + B ) ( A ‾ + C ) = A A ‾ + A C + B A ‾ + B C = A C + B A ‾ + B C F = (A+B)(\overline{A}+C)=A\overline{A}+AC+B\overline{A}+BC=AC+B\overline{A}+BC F=(A+B)(A+C)=AA+AC+BA+BC=AC+BA+BC。这样就不存在互补项,在一定程度上,避免了竞争和冒险。
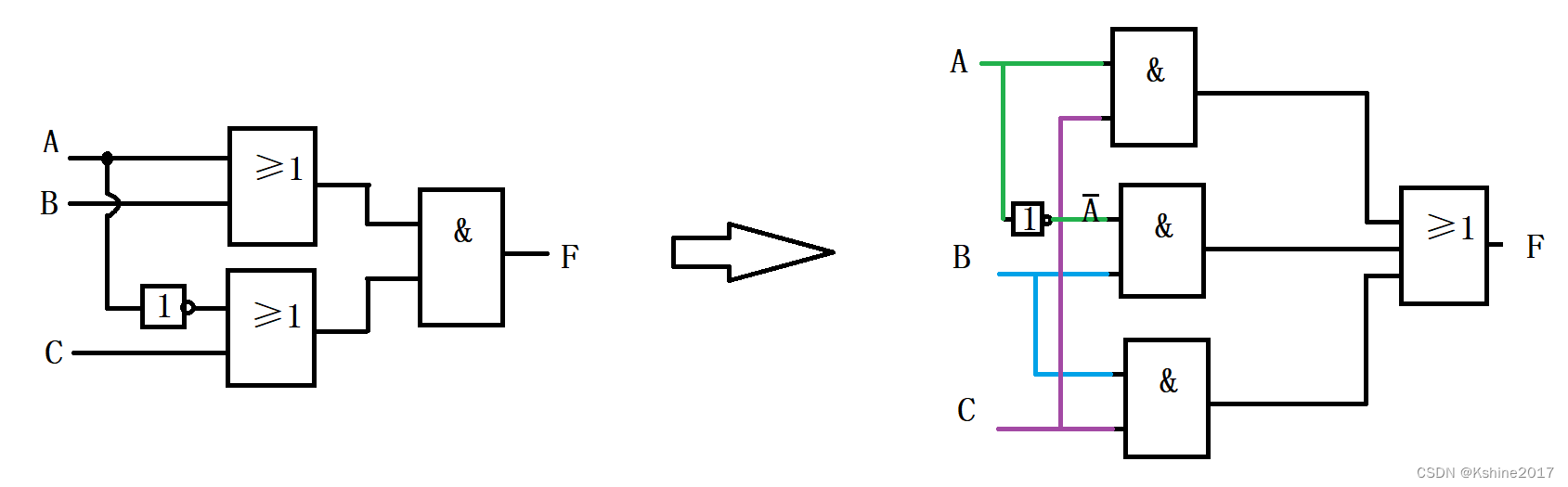
2. 增加乘积项以避免互补项相加
- 上文所述, F = A C + B A ‾ + B C F =AC+B\overline{A}+BC F=AC+BA+BC,当B=C=1时, F = A + A ‾ + 1 = 1 F = A+\overline{A}+1 =1 F=A+A+1=1。此处的BC乘积项=1,起到了作用,避免了互补项相加的竞争冒险。
- 根据常用恒等式“或”运算(2.1节), A B + A ‾ C + B C = A B + A ‾ C AB + \overline{A} C + BC = AB + \overline{A} C AB+AC+BC=AB+AC。
- 当遇到逻辑函数
L
=
A
C
+
B
C
‾
L=AC + B\overline{C}
L=AC+BC这种形式时,我们可以增加乘积项
A
B
AB
AB。
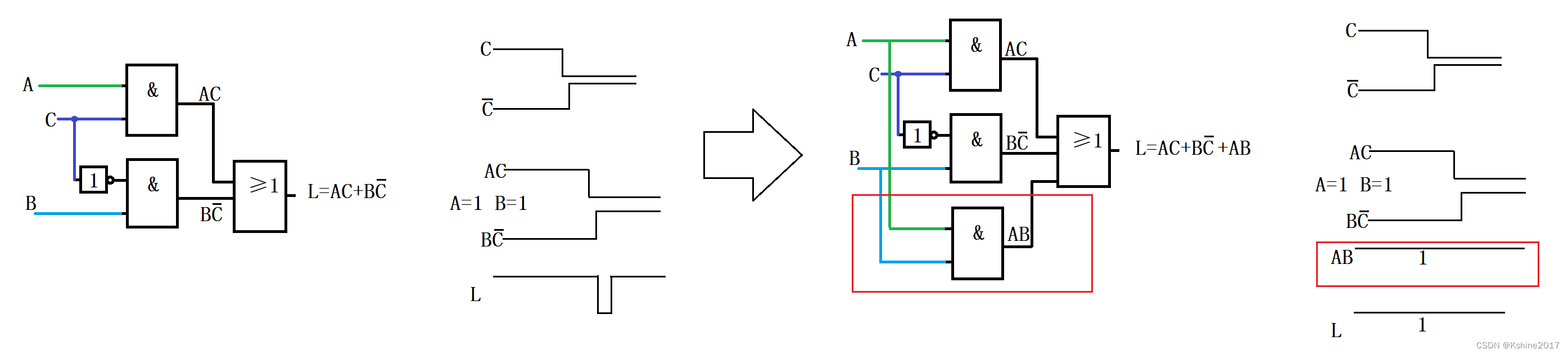
3. 输出端并联电容器
- 针对速度较慢的工作场景。
- 电容值4~20pF。对冒险窄脉冲起到 “平波”的作用。
- 缺点:会使输出波形上升沿和下降沿,变得缓慢。
4.4 (学习重点)若干典型的组合逻辑集成电路
- 编码器,译码器,数据选择器,数据分配器,数值比较器,算术/逻辑运算单元。
4.4.1 编码器
1. 定义和工作原理
- 用一个二进制代码表示特定含义的信息,称为编码。
- 具有编码功能的逻辑电路,称为编码器。
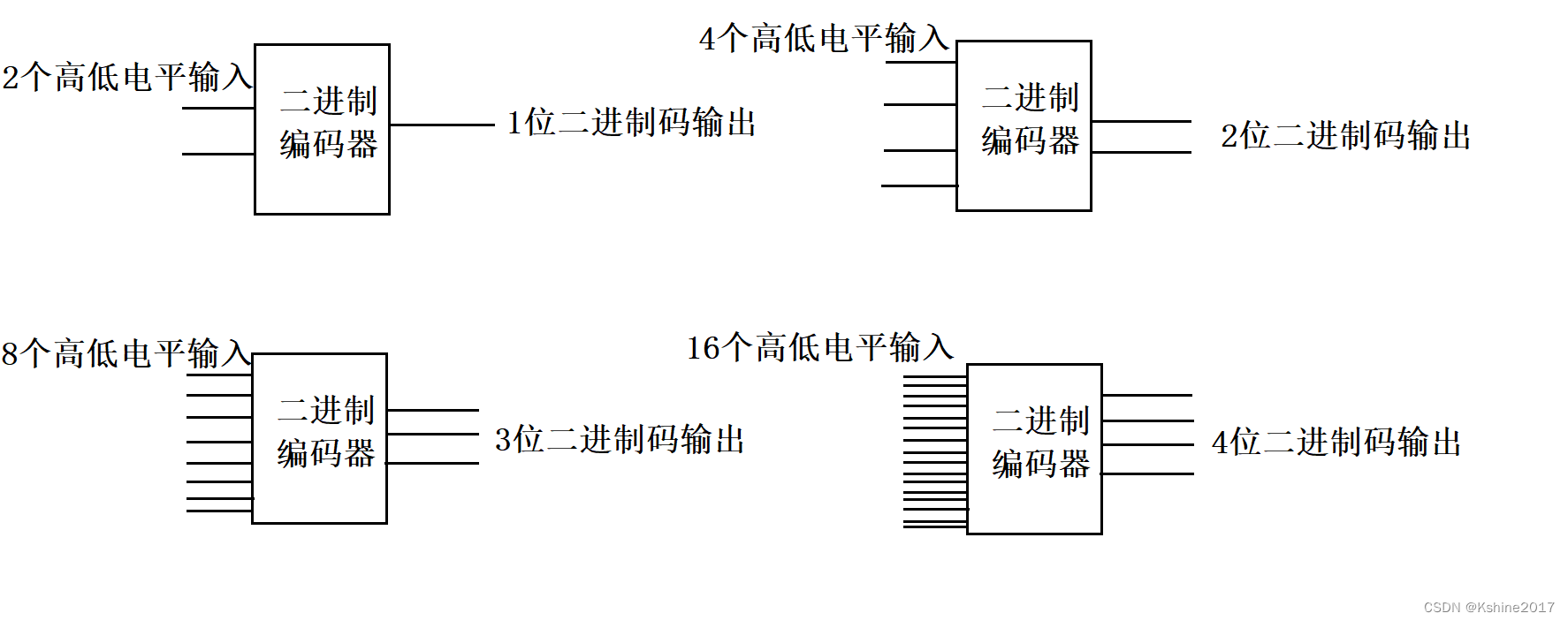
(1)普通译码器(4线-2线编码器)
- 4个输入 I 0 I 1 I 2 I 3 I_0 I_1 I_2 I_3 I0I1I2I3,高电平有效信号。
- 2个输出 Y 1 Y 0 Y_1Y_0 Y1Y0。
- 前提:任何时刻, I 0 I 1 I 2 I 3 I_0 I_1 I_2 I_3 I0I1I2I3只能有一个值为1。并且有一个对应的二进制码 Y 1 Y 0 Y_1Y_0 Y1Y0。
- 如下表所示,除此4输入的4种取值组合之外,其他12种组合对应的输出,都是00。
| I 0 I_0 I0 | I 1 I_1 I1 | I 2 I_2 I2 | I 3 I_3 I3 | Y 1 Y_1 Y1 | Y 0 Y_0 Y0 |
|---|---|---|---|---|---|
| 1 | 0 | 0 | 0 | 0 | 0 |
| 0 | 1 | 0 | 0 | 0 | 1 |
| 0 | 0 | 1 | 0 | 1 | 0 |
| 0 | 0 | 0 | 1 | 1 | 1 |
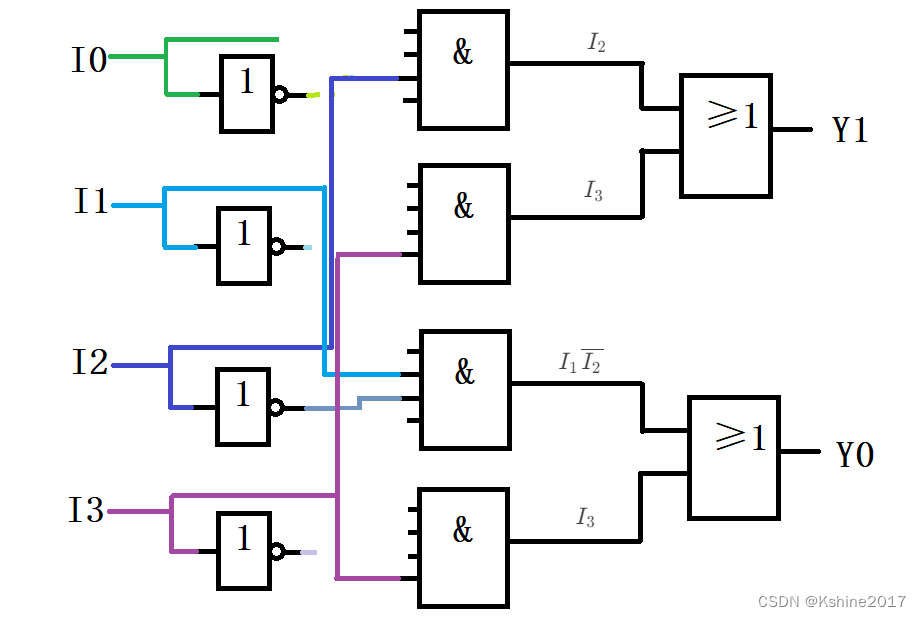
- 逻辑表达式与逻辑图
Y 1 = I 0 ‾ I 1 ‾ I 2 I 3 ‾ + I 0 ‾ I 1 ‾ I 2 ‾ I 3 Y_1 = \overline{I_0}\overline{I_1}I_2\overline{I_3}+\overline{I_0}\overline{I_1}\overline{I_2}I_3 Y1=I0I1I2I3+I0I1I2I3
Y 0 = I 0 ‾ I 1 I 2 ‾ I 3 ‾ + I 0 ‾ I 1 ‾ I 2 ‾ I 3 Y_0 = \overline{I_0}I_1\overline{I_2}\overline{I_3}+\overline{I_0}\overline{I_1}\overline{I_2}I_3 Y0=I0I1I2I3+I0I1I2I3
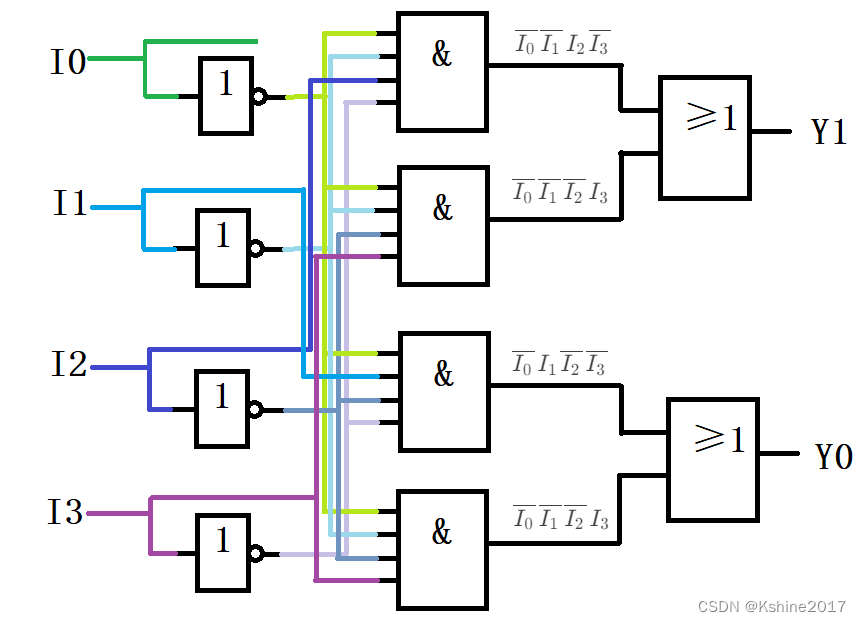
- 额外问题:如果4个输入中,同时有2位以上取值为1,输出会出现错误编码。
例如: I 2 = I 3 = 1 I_2=I_3=1 I2=I3=1时, Y 1 Y 0 = 0 Y_1Y_0=0 Y1Y0=0。 - 针对这个问题,可以通过增加优先级的方式,规定好轻重缓急和优先顺序。
(2)优先编码器
- 在上述基础上,列出真值表。
| I 0 I_0 I0 | I 1 I_1 I1 | I 2 I_2 I2 | I 3 I_3 I3 | Y 1 Y_1 Y1 | Y 0 Y_0 Y0 |
|---|---|---|---|---|---|
| 1 | 0 | 0 | 0 | 0 | 0 |
| X | 1 | 0 | 0 | 0 | 1 |
| X | X | 1 | 0 | 1 | 0 |
| X | X | X | 1 | 1 | 1 |
- 逻辑表达式:
Y 1 = I 2 I 3 ‾ + I 3 = I 2 + I 3 Y_1 = I_2\overline{I_3}+I_3= I_2+I_3 Y1=I2I3+I3=I2+I3
Y 0 = I 1 I 2 ‾ I 3 ‾ + I 3 = I 1 I 2 ‾ + I 3 Y_0 = I_1\overline{I_2}\overline{I_3}+I_3=I_1\overline{I_2}+I_3 Y0=I1I2I3+I3=I1I2+I3
(3)输出值有效
- 额外问题:当 I 0 = 1 或 I 0 = 1 I_0=1或I_0=1 I0=1或I0=1时,始终 Y 1 Y 0 = 0 Y_1Y_0=0 Y1Y0=0。输入不同,输出相同,无法区分有效的输出0( I 0 = 1 I_0=1 I0=1)和无效的输出0。
- 针对该问题,可以增加一个表示“输出值有效”的输出标志值GS。
- 例如,如下的8421BCD编码器。真值表的第一行和第二行,都是0000,只有当GS==1时,表示此时的ABCD是有效的代码。
| S 9 S_9 S9 | S 8 S_8 S8 | S 7 S_7 S7 | S 6 S_6 S6 | S 5 S_5 S5 | S 4 S_4 S4 | S 3 S_3 S3 | S 2 S_2 S2 | S 1 S_1 S1 | S 0 S_0 S0 | A A A | B B B | C C C | D D D | G S GS GS | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | |
| 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 1 | |
| 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 0 | 1 | 0 | 0 | 0 | 1 | 1 | |
| 1 | 1 | 1 | 1 | 1 | 1 | 1 | 0 | 1 | 1 | 0 | 0 | 1 | 0 | 1 | |
| 1 | 1 | 1 | 1 | 1 | 1 | 0 | 1 | 1 | 1 | 0 | 0 | 1 | 1 | 1 | |
| 1 | 1 | 1 | 1 | 1 | 0 | 1 | 1 | 1 | 1 | 0 | 1 | 0 | 0 | 1 | |
| 1 | 1 | 1 | 1 | 0 | 1 | 1 | 1 | 1 | 1 | 0 | 1 | 0 | 1 | 1 | |
| 1 | 1 | 1 | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 0 | 1 | 1 | 0 | 1 | |
| 1 | 1 | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 0 | 1 | 1 | 1 | 1 | |
| 1 | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 0 | 0 | 0 | 1 | |
| 0 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 0 | 0 | 1 | 1 |
2. 集成电路优先编码器
-
典型:CD4532优先编码器(已停产)

-
优先编码器 I 7 优先级最高, I 0 优先级最低。 优先编码器 I_7优先级最高,I_0优先级最低。 优先编码器I7优先级最高,I0优先级最低。
- 只有当EI=1时,编码器工作。
- EI=0时,禁止编码器工作(输出全低电平)。
-
当EI=1时,所有的输入都为低电平时,找不到更低的优先级输入高电平,此时输出000。此时EO=1。
-
只有在EI=1,且所有输入端都为0时,EO=1。专用于与另一片器件的EI级联。
-
在EI=1,输入端至少一个为高电平1,GS=1。
-
具体逻辑表达式和逻辑框图见书中内容。
| E I 允许编码 EI允许编码 EI允许编码 | I 7 I_7 I7 | I 6 I_6 I6 | I 5 I_5 I5 | I 4 I_4 I4 | I 3 I_3 I3 | I 2 I_2 I2 | I 1 I_1 I1 | I 0 I_0 I0 | Y 2 Y_2 Y2 | Y 1 Y_1 Y1 | Y 0 Y_0 Y0 | G S 有输入 1 GS有输入1 GS有输入1 | E O 输入全 0 EO输入全0 EO输入全0 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | x | x | x | x | x | x | x | x | 0 | 0 | 0 | 0 | 0 | |
| 1 | 1 | x | x | x | x | x | x | x | 1 | 1 | 1 | 1 | 0 | |
| 1 | 0 | 1 | x | x | x | x | x | x | 1 | 1 | 0 | 1 | 0 | |
| 1 | 0 | 0 | 1 | x | x | x | x | x | 1 | 0 | 1 | 1 | 0 | |
| 1 | 0 | 0 | 0 | 1 | x | x | x | x | 1 | 0 | 0 | 1 | 0 | |
| 1 | 0 | 0 | 0 | 0 | 1 | x | x | x | 0 | 1 | 1 | 1 | 0 | |
| 1 | 0 | 0 | 0 | 0 | 0 | 1 | x | x | 0 | 1 | 0 | 1 | 0 | |
| 1 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | x | 0 | 0 | 1 | 1 | 0 | |
| 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 1 | 0 | |
| 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 |

-
当 E I 1 = 0 时,片 1 被禁用。 Y 2 Y 1 Y 0 = = 000 , G S 1 = 0 , E O 1 = 0 。 E I 0 = 0 ,片 0 也被禁用。 当EI_1=0时,片1被禁用。Y_2Y_1Y_0==000,GS_1=0,EO_1=0。EI_0=0,片0也被禁用。 当EI1=0时,片1被禁用。Y2Y1Y0==000,GS1=0,EO1=0。EI0=0,片0也被禁用。
- 此时 G S 0 = 0 。 L 3 L 2 L 1 L 0 = 0000 。 G S = G S 1 + G S 0 = 0 , 此时GS_0=0。L_3L_2L_1L_0=0000。GS = GS_1+GS_0=0, 此时GS0=0。L3L2L1L0=0000。GS=GS1+GS0=0,
- 此时为 无效编码。
-
当 E I 1 = 1 时,片 1 允许编码,若 I 15 − I 8 = 000...000 ,此时 E O 1 = 1 ,从而 E I 0 = 1 。片 0 允许编码。可知,片 1 编码的优先级高于片 0 编码 当EI_1=1时,片1允许编码,若I_{15} - I_8 = 000...000,此时EO_1=1,从而EI_0=1。片0允许编码。可知,片1编码的优先级高于片0编码 当EI1=1时,片1允许编码,若I15−I8=000...000,此时EO1=1,从而EI0=1。片0允许编码。可知,片1编码的优先级高于片0编码。
- 此时 L 3 = G S 1 = 0 , L 2 = Y 2 1 + Y 2 0 = Y 2 0 , L 1 = Y 1 1 + Y 1 0 = Y 1 0 , L 0 = Y 0 1 + Y 0 0 = Y 0 0 此时L_3=GS_1=0 ,L2=Y2_1+Y2_0=Y2_0,L1=Y1_1+Y1_0=Y1_0,L0=Y0_1+Y0_0=Y0_0 此时L3=GS1=0,L2=Y21+Y20=Y20,L1=Y11+Y10=Y10,L0=Y01+Y00=Y00。
- 输出的编码范围是 0000 − 0111 输出的编码范围是0000-0111 输出的编码范围是0000−0111。
-
当 E I 1 = 1 时,片 1 允许编码,若 I 15 − I 8 至少有一个 1 ,此时 E O 1 = 0 , 从而 E I 0 = 0 ,片 0 禁止编码。 当EI_1=1时,片1允许编码,若I_{15} - I_8 至少有一个1,此时EO_1=0,从而EI_0=0,片0禁止编码。 当EI1=1时,片1允许编码,若I15−I8至少有一个1,此时EO1=0,从而EI0=0,片0禁止编码。
- 此时 L 3 = G S 1 = 1 , L 2 = Y 2 1 + Y 2 0 = Y 2 1 , L 1 = Y 1 1 + Y 1 0 = Y 1 1 , L 0 = Y 0 1 + Y 0 0 = Y 0 1 此时L_3=GS_1=1,L2=Y2_1+Y2_0=Y2_1,L1=Y1_1+Y1_0=Y1_1,L0=Y0_1+Y0_0=Y0_1 此时L3=GS1=1,L2=Y21+Y20=Y21,L1=Y11+Y10=Y11,L0=Y01+Y00=Y01
- 输出编码的范围是 1000 − 1111 输出编码的范围是1000-1111 输出编码的范围是1000−1111。
| E I 1 允许编码 EI_1允许编码 EI1允许编码 | E I 0 允许编码 EI_0允许编码 EI0允许编码 | I 15 I_{15} I15 | I 14 I_{14} I14 | I 13 I_{13} I13 | I 12 I_{12} I12 | I 11 I_{11} I11 | I 10 I_{10} I10 | I 9 I_{9} I9 | I 8 I_8 I8 | I 7 I_7 I7 | I 6 I_6 I6 | I 5 I_5 I5 | I 4 I_4 I4 | I 3 I_3 I3 | I 2 I_2 I2 | I 1 I_1 I1 | I 0 I_0 I0 | Y 2 1 Y2_1 Y21 | Y 1 1 Y1_1 Y11 | Y 0 1 Y0_1 Y01 | Y 2 0 Y2_0 Y20 | Y 1 0 Y1_0 Y10 | Y 0 0 Y0_0 Y00 | E O 1 输入全 0 EO_1输入全0 EO1输入全0 | E O 0 输入全 0 EO_0输入全0 EO0输入全0 | G S 1 有输入 1 GS_1有输入1 GS1有输入1 | G S 0 有输入 0 GS_0有输入0 GS0有输入0 | L 3 L_3 L3 | L 2 L_2 L2 | L 1 L_1 L1 | L 0 L_0 L0 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0(片1禁用 ) | E I 0 = E O 1 = 0 EI_0=EO_1=0 EI0=EO1=0(片0禁用 ) | x | x | x | x | x | x | x | x | x | x | x | x | x | x | x | x | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | |
| 1 | 0 | 1 | x | x | x | x | x | x | x | x | x | x | x | x | x | x | x | 1 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 1 (片1有输入) | 0 | 1 L 3 = G S 1 L_3 =GS_1 L3=GS1 | 1 L 2 = Y 2 1 L_2 =Y2_1 L2=Y21 | 1 L 1 = Y 1 1 L_1 =Y1_1 L1=Y11 | 1 L 0 = Y 0 1 L_0 =Y0_1 L0=Y01 | |
| 1 | 0 | 0 | 1 | x | x | x | x | x | x | x | x | x | x | x | x | x | x | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 1 | 1 | 1 | 0 | |
| 1 | 0 | 0 | 0 | 1 | x | x | x | x | x | x | x | x | x | x | x | x | x | 1 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 1 | 1 | 0 | 1 | |
| 1 | 0 | 0 | 0 | 0 | 1 | x | x | x | x | x | x | x | x | x | x | x | x | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 1 | 1 | 0 | 0 | |
| 1 | 0 | 0 | 0 | 0 | 0 | 1 | x | x | x | x | x | x | x | x | x | x | x | 0 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 1 | 0 | 1 | 1 | |
| 1 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | x | x | x | x | x | x | x | x | x | x | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | |
| 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | x | x | x | x | x | x | x | x | x | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 1 | 0 | 0 | 1 | |
| 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | x | x | x | x | x | x | x | x | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 1 | 0 | 0 | 0 | |
| 1 | E I 0 = E O 1 = 1 EI_0=EO_1=1 EI0=EO1=1(片0工作 ) | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | x | x | x | x | x | x | x | 0 | 0 | 0 | 1 | 1 | 1 | 1(片1输入全0) | 0 | 0(片1无效编码) | 1 | 0 L 3 = G S 1 L_3 =GS_1 L3=GS1 | 1 L 2 = Y 2 0 L_2 =Y2_0 L2=Y20 | 1 L 1 = Y 1 0 L_1 =Y1_0 L1=Y10 | 1 L 0 = Y 0 0 L_0 =Y0_0 L0=Y00 | |
| 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | x | x | x | x | x | x | 0 | 0 | 0 | 1 | 1 | 0 | 1 | 0 | 0 | 1 | 0 | 1 | 1 | 0 | |
| 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | x | x | x | x | x | 0 | 0 | 0 | 1 | 1 | 1 | 1 | 0 | 0 | 1 | 0 | 1 | 0 | 1 | |
| 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | x | x | x | x | 0 | 0 | 0 | 1 | 1 | 1 | 1 | 0 | 0 | 1 | 0 | 1 | 0 | 0 | |
| 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | x | x | x | 0 | 0 | 0 | 1 | 1 | 1 | 1 | 0 | 0 | 1 | 0 | 0 | 1 | 1 | |
| 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | x | x | 0 | 0 | 0 | 1 | 1 | 1 | 1 | 0 | 0 | 1 | 0 | 0 | 1 | 0 | |
| 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | x | 0 | 0 | 0 | 1 | 1 | 1 | 1 | 0 | 0 | 1 | 0 | 0 | 0 | 1 | |
| 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 1 | 1 | 1 | 1 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | |
| 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 1 | 1(片0输入全0) | 0 | 0(片0无效编码) | 0 | 0 | 0 | 0 |
4.4.2 译码器
- 138译码器。
- 151数据选择器。
1. 定义和功能
- 有两种类型的译码器:
- 唯一地址译码器:将一系列代码转换成与之一一对应的有效信号。(例如计算机对存储单元地址的译码,将地址代码转换成一个有效信号,选中对应的存储单元)
- 代码变换器:将一种代码转换成另一种代码。
(1)二进制译码器
- n个输入端
- 2 n 2^n 2n个输出端
- 1个使能端
(2)2线-4线译码器
- 输出端,低电平有效

- 真值表
| 输入 | 输出 | |||||
| /E | A_1 | A_0 | /Y_3 | /Y_2 | /Y_1 | /Y_0 |
| 1 禁止 | X | X | 1 | 1 | 1 | 1 |
| 0 使能 | 0 | 0 | 1 | 1 | 1 | 0 低有效 |
| 0 使能 | 0 | 1 | 1 | 1 | 0低有效 | 1 |
| 0 使能 | 1 | 0 | 1 | 0 低有效 | 1 | 1 |
| 0 使能 | 1 | 1 | 0 低有效 | 1 | 1 | 1 |
- 逻辑表达式(非门和与非门的表达形式)
Y
0
‾
=
E
‾
‾
⋅
A
1
‾
⋅
A
0
‾
‾
\overline{Y_0} = \overline{\overline{\overline{E}}·\overline{A_1}·\overline{A_0}}
Y0=E⋅A1⋅A0 //00
Y
1
‾
=
E
‾
‾
⋅
A
1
‾
⋅
A
0
‾
\overline{Y_1} = \overline{\overline{\overline{E}}·\overline{A_1}·A_0}
Y1=E⋅A1⋅A0 //01
Y
2
‾
=
E
‾
‾
⋅
A
1
⋅
A
0
‾
‾
\overline{Y_2} = \overline{\overline{\overline{E}}·A_1·\overline{A_0}}
Y2=E⋅A1⋅A0 //10
Y
3
‾
=
E
‾
‾
⋅
A
1
⋅
A
0
‾
\overline{Y_3} = \overline{\overline{\overline{E}}·A_1·A_0}
Y3=E⋅A1⋅A0 //11
- 2线-4线译码器的逻辑图

2. 集成电路译码器
(1)二进制译码器
2线-4线译码器x2
- 用74x139表示CMOS型74HC139或者TTL型74LS139。
- 74x139是“双2线-4线译码器”。
- 两个独立的译码器封装在一个集成芯片中。(详细见上文)

3线-8线译码器
- 用74x138表示CMOS型74HC138或者TTL型74LS138。
- 74x138是3线-8线译码器。
- 利用3线-8线译码器可以构成4线-16线译码器、5线-32线译码器、6线-64线译码器。
- 当 E 3 = 1 , E 2 ‾ = E 1 ‾ = 0 E_3=1,\overline{E_2}=\overline{E_1}=0 E3=1,E2=E1=0时,译码器处于工作状态。

- 仿照前文,可以推出“3线-8线译码器”的逻辑表达式。
Y
0
‾
=
E
3
⋅
E
2
‾
‾
⋅
E
1
‾
‾
⋅
A
2
‾
⋅
A
1
‾
⋅
A
0
‾
‾
\overline{Y_0} = \overline{E_3·\overline{\overline{E_2}}·\overline{\overline{E_1}}·\overline{A_2}·\overline{A_1}·\overline{A_0}}
Y0=E3⋅E2⋅E1⋅A2⋅A1⋅A0 //000
Y
1
‾
=
E
3
⋅
E
2
‾
‾
⋅
E
1
‾
‾
⋅
A
2
‾
⋅
A
1
‾
⋅
A
0
‾
\overline{Y_1} = \overline{E_3·\overline{\overline{E_2}}·\overline{\overline{E_1}}·\overline{A_2}·\overline{A_1}·A_0}
Y1=E3⋅E2⋅E1⋅A2⋅A1⋅A0 //001
Y
2
‾
=
E
3
⋅
E
2
‾
‾
⋅
E
1
‾
‾
⋅
A
2
‾
⋅
A
1
⋅
A
0
‾
‾
\overline{Y_2} = \overline{E_3·\overline{\overline{E_2}}·\overline{\overline{E_1}}·\overline{A_2}·A_1·\overline{A_0}}
Y2=E3⋅E2⋅E1⋅A2⋅A1⋅A0 //010
Y
3
‾
=
E
3
⋅
E
2
‾
‾
⋅
E
1
‾
‾
⋅
A
2
‾
⋅
A
1
⋅
A
0
‾
\overline{Y_3} = \overline{E_3·\overline{\overline{E_2}}·\overline{\overline{E_1}}·\overline{A_2}·A_1·A_0}
Y3=E3⋅E2⋅E1⋅A2⋅A1⋅A0 //011
Y
4
‾
=
E
3
⋅
E
2
‾
‾
⋅
E
1
‾
‾
⋅
A
2
⋅
A
1
‾
⋅
A
0
‾
‾
\overline{Y_4} = \overline{E_3·\overline{\overline{E_2}}·\overline{\overline{E_1}}·A_2·\overline{A_1}·\overline{A_0}}
Y4=E3⋅E2⋅E1⋅A2⋅A1⋅A0 //100
Y
5
‾
=
E
3
⋅
E
2
‾
‾
⋅
E
1
‾
‾
⋅
A
2
⋅
A
1
‾
⋅
A
0
‾
\overline{Y_5} = \overline{E_3·\overline{\overline{E_2}}·\overline{\overline{E_1}}·A_2·\overline{A_1}·A_0}
Y5=E3⋅E2⋅E1⋅A2⋅A1⋅A0 //101
Y
6
‾
=
E
3
⋅
E
2
‾
‾
⋅
E
1
‾
‾
⋅
A
2
⋅
A
1
⋅
A
0
‾
‾
\overline{Y_6} = \overline{E_3·\overline{\overline{E_2}}·\overline{\overline{E_1}}·A_2·A_1·\overline{A_0}}
Y6=E3⋅E2⋅E1⋅A2⋅A1⋅A0 //110
Y
7
‾
=
E
3
⋅
E
2
‾
‾
⋅
E
1
‾
‾
⋅
A
2
⋅
A
1
⋅
A
0
‾
\overline{Y_7} = \overline{E_3·\overline{\overline{E_2}}·\overline{\overline{E_1}}·A_2·A_1·A_0}
Y7=E3⋅E2⋅E1⋅A2⋅A1⋅A0 //111
5先-32线译码器
- 利用74x139和74x138构成“5线-32线译码器”

3线-8线译码器实现逻辑函数
- 逻辑函数是 L = A ‾ ⋅ C ‾ + A ⋅ B L=\overline{A}·\overline{C}+A·B L=A⋅C+A⋅B
- 3线-8线译码器的输入,可以定义为A、B、C。
- 3线-8线译码器的输出,实际就是A、B、C的各种最小项情况一一对应的8线输出。
- 任何ABC组合,只会有一路输出为有效电平。
- L实际就是A、B、C组合的几种情况的集合。
L = A ‾ ⋅ C ‾ + A ⋅ B = A ‾ ⋅ B ‾ ⋅ C ‾ + A ‾ ⋅ B ⋅ C ‾ + A ⋅ B ⋅ C ‾ + A B C = m 0 + m 2 + m 6 + m 7 L=\overline{A}·\overline{C}+A·B =\overline{A}·\overline{B}·\overline{C}+\overline{A}·B·\overline{C} + A·B·\overline{C}+ABC = m_0+m_2+m_6+m_7 L=A⋅C+A⋅B=A⋅B⋅C+A⋅B⋅C+A⋅B⋅C+ABC=m0+m2+m6+m7
Y
0
‾
=
E
3
⋅
E
2
‾
‾
⋅
E
1
‾
‾
⋅
A
2
‾
⋅
A
1
‾
⋅
A
0
‾
‾
=
E
3
⋅
E
2
‾
‾
⋅
E
1
‾
‾
⋅
m
0
‾
\overline{Y_0} = \overline{E_3·\overline{\overline{E_2}}·\overline{\overline{E_1}}·\overline{A_2}·\overline{A_1}·\overline{A_0}} = \overline{E_3·\overline{\overline{E_2}}·\overline{\overline{E_1}}·m_0}
Y0=E3⋅E2⋅E1⋅A2⋅A1⋅A0=E3⋅E2⋅E1⋅m0 //000
Y
1
‾
=
E
3
⋅
E
2
‾
‾
⋅
E
1
‾
‾
⋅
A
2
‾
⋅
A
1
‾
⋅
A
0
‾
=
E
3
⋅
E
2
‾
‾
⋅
E
1
‾
‾
⋅
m
1
‾
\overline{Y_1} = \overline{E_3·\overline{\overline{E_2}}·\overline{\overline{E_1}}·\overline{A_2}·\overline{A_1}·A_0} = \overline{E_3·\overline{\overline{E_2}}·\overline{\overline{E_1}}·m_1}
Y1=E3⋅E2⋅E1⋅A2⋅A1⋅A0=E3⋅E2⋅E1⋅m1 //001
Y
2
‾
=
E
3
⋅
E
2
‾
‾
⋅
E
1
‾
‾
⋅
A
2
‾
⋅
A
1
⋅
A
0
‾
‾
=
E
3
⋅
E
2
‾
‾
⋅
E
1
‾
‾
⋅
m
2
‾
\overline{Y_2} = \overline{E_3·\overline{\overline{E_2}}·\overline{\overline{E_1}}·\overline{A_2}·A_1·\overline{A_0}}= \overline{E_3·\overline{\overline{E_2}}·\overline{\overline{E_1}}·m_2}
Y2=E3⋅E2⋅E1⋅A2⋅A1⋅A0=E3⋅E2⋅E1⋅m2 //010
Y
3
‾
=
E
3
⋅
E
2
‾
‾
⋅
E
1
‾
‾
⋅
A
2
‾
⋅
A
1
⋅
A
0
‾
=
E
3
⋅
E
2
‾
‾
⋅
E
1
‾
‾
⋅
m
3
‾
\overline{Y_3} = \overline{E_3·\overline{\overline{E_2}}·\overline{\overline{E_1}}·\overline{A_2}·A_1·A_0}= \overline{E_3·\overline{\overline{E_2}}·\overline{\overline{E_1}}·m_3}
Y3=E3⋅E2⋅E1⋅A2⋅A1⋅A0=E3⋅E2⋅E1⋅m3 //011
Y
4
‾
=
E
3
⋅
E
2
‾
‾
⋅
E
1
‾
‾
⋅
A
2
⋅
A
1
‾
⋅
A
0
‾
‾
=
E
3
⋅
E
2
‾
‾
⋅
E
1
‾
‾
⋅
m
4
‾
\overline{Y_4} = \overline{E_3·\overline{\overline{E_2}}·\overline{\overline{E_1}}·A_2·\overline{A_1}·\overline{A_0}}= \overline{E_3·\overline{\overline{E_2}}·\overline{\overline{E_1}}·m_4}
Y4=E3⋅E2⋅E1⋅A2⋅A1⋅A0=E3⋅E2⋅E1⋅m4 //100
Y
5
‾
=
E
3
⋅
E
2
‾
‾
⋅
E
1
‾
‾
⋅
A
2
⋅
A
1
‾
⋅
A
0
‾
=
E
3
⋅
E
2
‾
‾
⋅
E
1
‾
‾
⋅
m
5
‾
\overline{Y_5} = \overline{E_3·\overline{\overline{E_2}}·\overline{\overline{E_1}}·A_2·\overline{A_1}·A_0}= \overline{E_3·\overline{\overline{E_2}}·\overline{\overline{E_1}}·m_5}
Y5=E3⋅E2⋅E1⋅A2⋅A1⋅A0=E3⋅E2⋅E1⋅m5 //101
Y
6
‾
=
E
3
⋅
E
2
‾
‾
⋅
E
1
‾
‾
⋅
A
2
⋅
A
1
⋅
A
0
‾
‾
=
E
3
⋅
E
2
‾
‾
⋅
E
1
‾
‾
⋅
m
6
‾
\overline{Y_6} = \overline{E_3·\overline{\overline{E_2}}·\overline{\overline{E_1}}·A_2·A_1·\overline{A_0}}= \overline{E_3·\overline{\overline{E_2}}·\overline{\overline{E_1}}·m_6}
Y6=E3⋅E2⋅E1⋅A2⋅A1⋅A0=E3⋅E2⋅E1⋅m6 //110
Y
7
‾
=
E
3
⋅
E
2
‾
‾
⋅
E
1
‾
‾
⋅
A
2
⋅
A
1
⋅
A
0
‾
=
E
3
⋅
E
2
‾
‾
⋅
E
1
‾
‾
⋅
m
7
‾
\overline{Y_7} = \overline{E_3·\overline{\overline{E_2}}·\overline{\overline{E_1}}·A_2·A_1·A_0}= \overline{E_3·\overline{\overline{E_2}}·\overline{\overline{E_1}}·m_7}
Y7=E3⋅E2⋅E1⋅A2⋅A1⋅A0=E3⋅E2⋅E1⋅m7 //111
-
确保 E 3 = 1 , E 2 = 0 , E 1 = 0 确保E_3=1,E_2=0,E_1=0 确保E3=1,E2=0,E1=0,也就是说 Y 0 ‾ = m 0 ‾ , Y 2 ‾ = m 2 ‾ , Y 6 ‾ = m 6 ‾ , Y 7 ‾ = m 7 ‾ \overline{Y_0}=\overline{m_0},\overline{Y_2}=\overline{m_2},\overline{Y_6}=\overline{m_6},\overline{Y_7}=\overline{m_7} Y0=m0,Y2=m2,Y6=m6,Y7=m7。
-
根据反演律变换逻辑函数
L = L ‾ ‾ = m 0 + m 2 + m 6 + m 7 ‾ ‾ = m 0 ‾ ⋅ m 2 ‾ ⋅ m 6 ‾ ⋅ m 7 ‾ ‾ = m 0 + m 2 + m 6 + m 7 ‾ ‾ = Y 0 ‾ ⋅ Y 2 ‾ ⋅ Y 6 ‾ ⋅ Y 7 ‾ ‾ L=\overline{\overline{L}} = \overline{\overline{m_0+m_2+m_6+m_7}} = \overline{\overline{m_0}·\overline{m_2}·\overline{m_6}·\overline{m_7}} = \overline{\overline{m_0+m_2+m_6+m_7}} = \overline{\overline{Y_0}·\overline{Y_2}·\overline{Y_6}·\overline{Y_7}} L=L=m0+m2+m6+m7=m0⋅m2⋅m6⋅m7=m0+m2+m6+m7=Y0⋅Y2⋅Y6⋅Y7 -
得到逻辑图

(2)二-十进制译码器
-
774HC42
-
4个输入端
-
10个输出端,输出低电平有效,对应十进制数0~9。

-
4个输入端,共有16种情况
-
只有 m 0 , m 1 , m 2 . . . . . . m 9 m_0 ,m_1,m_2......m_9 m0,m1,m2......m9为有效的输入(对应的输出引脚输出低0,其余输出高1)。
-
其余6中 m 10 , m 11 , m 12 . . . . . . m 15 m_{10} ,m_{11},m_{12}......m_{15} m10,m11,m12......m15为无有效译码输出(无效时,输出全为高1)。
-
画出74HC42的输入、输出波形图。

- 如果DCBA循环输入0000-1001,会在 Y 0 ‾ 到 Y 9 ‾ \overline{Y_0}到\overline{Y_9} Y0到Y9上循环输出“顺序脉冲信号”。
- 译码器可以构成顺序脉冲产生电路。

(3)七段显示译码器
-
数码管显示原理

-
集成七段显示译码器。74HC4511(共阴极)(高电平点亮)
-
L E LE LE锁存使能
-
L T ‾ \overline{LT} LT灯测试输入,当 L T ‾ = 0 \overline{LT}=0 LT=0时,a-g全部输出1,显示字形“8”。
-
B L ‾ \overline{BL} BL灭灯输入,当 L T ‾ = 1 ,且 B L ‾ = 1 \overline{LT}=1,且\overline{BL}=1 LT=1,且BL=1时,a-g全部输出0。可用于将不必要的显示的零“0”,熄灭。

-
D 3 D 2 D 1 D 0 D_3D_2D_1D_0 D3D2D1D0=0000时,对应输出字形“0”
-
D 3 D 2 D 1 D 0 D_3D_2D_1D_0 D3D2D1D0=0001时,对应输出字形“1”
-
D 3 D 2 D 1 D 0 D_3D_2D_1D_0 D3D2D1D0=0010时,对应输出字形“2”
-
D 3 D 2 D 1 D 0 D_3D_2D_1D_0 D3D2D1D0=0011时,对应输出字形“3”
-
D 3 D 2 D 1 D 0 D_3D_2D_1D_0 D3D2D1D0=0100时,对应输出字形“4”
-
D 3 D 2 D 1 D 0 D_3D_2D_1D_0 D3D2D1D0=0101时,对应输出字形“5”
-
D 3 D 2 D 1 D 0 D_3D_2D_1D_0 D3D2D1D0=0110时,对应输出字形“6”
-
D 3 D 2 D 1 D 0 D_3D_2D_1D_0 D3D2D1D0=0111时,对应输出字形“7”
-
D 3 D 2 D 1 D 0 D_3D_2D_1D_0 D3D2D1D0=1000时,对应输出字形“8”
-
D 3 D 2 D 1 D 0 D_3D_2D_1D_0 D3D2D1D0=1001时,对应输出字形“9”
-
1010-1111,熄灭
3. 数据分配器
-
一到多,将公共数据线的数据,根据需要送到不同的通道上。
-
类似“单刀多掷开关”
-
使用唯一地址译码器,实现数据分配器
-
举例,74x138集成3线-8线译码器。
-
E 1 ‾ 作为数据输入 \overline{E_1}作为数据输入 E1作为数据输入
-
Y 0 Y 1 Y 2 Y 3 Y 4 Y 5 Y 6 Y 7 Y_0 Y_1 Y_2Y_3Y_4Y_5Y_6Y_7 Y0Y1Y2Y3Y4Y5Y6Y7作为数据输出的8个通道

-
Y 2 ‾ = E 3 ⋅ E 2 ‾ ‾ ⋅ E 1 ‾ ‾ ⋅ A 2 ‾ ⋅ A 1 ⋅ A 0 ‾ ‾ \overline{Y_2} = \overline{E_3·\overline{\overline{E_2}}·\overline{\overline{E_1}}·\overline{A_2}·A_1·\overline{A_0}} Y2=E3⋅E2⋅E1⋅A2⋅A1⋅A0 //010
-
上图, E 3 = 1 , E 2 ‾ = 0 E_3=1,\overline{E_2}=0 E3=1,E2=0,当地址线 A 2 A 1 A 0 = 010 A_2A_1A_0=010 A2A1A0=010时, Y 2 ‾ = E 1 ‾ \overline{Y_2}=\overline{E_1} Y2=E1
-
同理可以得出:
当地址线 A 2 A 1 A 0 = 000 A_2A_1A_0=000 A2A1A0=000时, Y 0 ‾ = E 1 ‾ = D \overline{Y_0}=\overline{E_1}=D Y0=E1=D,其他 Y x = 1 Y_x=1 Yx=1。
当地址线 A 2 A 1 A 0 = 001 A_2A_1A_0=001 A2A1A0=001时, Y 1 ‾ = E 1 ‾ = D \overline{Y_1}=\overline{E_1}=D Y1=E1=D,其他 Y x = 1 Y_x=1 Yx=1。
当地址线 A 2 A 1 A 0 = 010 A_2A_1A_0=010 A2A1A0=010时, Y 2 ‾ = E 1 ‾ = D \overline{Y_2}=\overline{E_1}=D Y2=E1=D,其他 Y x = 1 Y_x=1 Yx=1。
当地址线 A 2 A 1 A 0 = 011 A_2A_1A_0=011 A2A1A0=011时, Y 3 ‾ = E 1 ‾ = D \overline{Y_3}=\overline{E_1}=D Y3=E1=D,其他 Y x = 1 Y_x=1 Yx=1。
当地址线 A 2 A 1 A 0 = 100 A_2A_1A_0=100 A2A1A0=100时, Y 4 ‾ = E 1 ‾ = D \overline{Y_4}=\overline{E_1}=D Y4=E1=D,其他 Y x = 1 Y_x=1 Yx=1。
当地址线 A 2 A 1 A 0 = 101 A_2A_1A_0=101 A2A1A0=101时, Y 5 ‾ = E 1 ‾ = D \overline{Y_5}=\overline{E_1}=D Y5=E1=D,其他 Y x = 1 Y_x=1 Yx=1。
当地址线 A 2 A 1 A 0 = 110 A_2A_1A_0=110 A2A1A0=110时, Y 6 ‾ = E 1 ‾ = D \overline{Y_6}=\overline{E_1}=D Y6=E1=D,其他 Y x = 1 Y_x=1 Yx=1。
当地址线 A 2 A 1 A 0 = 111 A_2A_1A_0=111 A2A1A0=111时, Y 7 ‾ = E 1 ‾ = D \overline{Y_7}=\overline{E_1}=D Y7=E1=D,其他 Y x = 1 Y_x=1 Yx=1。
4.4.3 数据选择器
1. 定义和功能
- 和上文4.4.2.3的"数据分配器",功能相反。
- 多到一。
- 例如,4选1数据选择器。

- E ‾ = 0 \overline{E}=0 E=0,允许工作。
- 当 S 1 = 0 , S 0 = 0 S_1=0,S_0=0 S1=0,S0=0时, Y = I 0 Y=I_0 Y=I0
- 当 S 1 = 0 , S 0 = 1 S_1=0,S_0=1 S1=0,S0=1时, Y = I 1 Y=I_1 Y=I1
- 当 S 1 = 1 , S 0 = 0 S_1=1,S_0=0 S1=1,S0=0时, Y = I 2 Y=I_2 Y=I2
- 当 S 1 = 1 , S 0 = 1 S_1=1,S_0=1 S1=1,S0=1时, Y = I 3 Y=I_3 Y=I3
2. 集成电路数据选择器
- 74x151:一-8选1-数据选择器。对应CMOS型74HC151,TTL型74LS151。
- 74x153:双-4选1-数据选择器。对应CMOS型74HC153,TTL型74LS153。
- 74x157:四-2选1-数据选择器。对应CMOS型74HC157,TTL型74LS157。
- 74x251:具有三态输出,当 E ‾ = 1 \overline{E}=1 E=1时,输出高阻状态。支持多个芯片输出端“线与”。
- 74x253:具有三态输出,当 E ‾ = 1 \overline{E}=1 E=1时,输出高阻状态。支持多个芯片输出端“线与”。
- 74x257:具有三态输出,当 E ‾ = 1 \overline{E}=1 E=1时,输出高阻状态。支持多个芯片输出端“线与”。
(1)74HC151
Y
=
S
2
‾
⋅
S
1
‾
⋅
S
0
‾
⋅
D
0
+
S
2
‾
⋅
S
1
‾
⋅
S
0
⋅
D
1
+
S
2
‾
⋅
S
1
⋅
S
0
‾
⋅
D
2
+
S
2
‾
⋅
S
1
⋅
S
0
⋅
D
3
+
S
2
⋅
S
1
‾
⋅
S
0
‾
⋅
D
4
+
S
2
⋅
S
1
‾
⋅
S
0
⋅
D
5
+
S
2
⋅
S
1
⋅
S
0
‾
⋅
D
6
+
S
2
⋅
S
1
⋅
S
0
⋅
D
7
Y=\overline{S_2}·\overline{S_1}·\overline{S_0}·D_0 +\overline{S_2}·\overline{S_1}·S_0·D_1 +\overline{S_2}·S_1·\overline{S_0}·D_2 +\overline{S_2}·S_1·S_0·D_3 +S_2·\overline{S_1}·\overline{S_0}·D_4 +S_2·\overline{S_1}·S_0·D_5 +S_2·S_1·\overline{S_0}·D_6 +S_2·S_1·S_0·D_7
Y=S2⋅S1⋅S0⋅D0+S2⋅S1⋅S0⋅D1+S2⋅S1⋅S0⋅D2+S2⋅S1⋅S0⋅D3+S2⋅S1⋅S0⋅D4+S2⋅S1⋅S0⋅D5+S2⋅S1⋅S0⋅D6+S2⋅S1⋅S0⋅D7

(2)数据选择器的应用
-
数据选择器的扩展。
- 输出位数扩展( Y 0 − > Y 1 Y 0 Y_0->Y_1Y_0 Y0−>Y1Y0)
- 输入位数扩展( D 7 D 6 D 5 D 4 D 3 D 2 D 1 D 0 − > D 15 D 14 D 13 D 12 D 11 D 10 D 9 D 8 D 7 D 6 D 5 D 4 D 3 D 2 D 1 D 0 D_7D_6D_5D_4D_3D_2D_1D_0->D_{15}D_{14}D_{13}D_{12}D_{11}D_{10}D_{9}D_{8}D_7D_6D_5D_4D_3D_2D_1D_0 D7D6D5D4D3D2D1D0−>D15D14D13D12D11D10D9D8D7D6D5D4D3D2D1D0)。
-
逻辑函数产生器
-
已知,8选1数据选择器。
Y = S 2 ‾ ⋅ S 1 ‾ ⋅ S 0 ‾ ⋅ D 0 + S 2 ‾ ⋅ S 1 ‾ ⋅ S 0 ⋅ D 1 + S 2 ‾ ⋅ S 1 ⋅ S 0 ‾ ⋅ D 2 + S 2 ‾ ⋅ S 1 ⋅ S 0 ⋅ D 3 + S 2 ⋅ S 1 ‾ ⋅ S 0 ‾ ⋅ D 4 + S 2 ⋅ S 1 ‾ ⋅ S 0 ⋅ D 5 + S 2 ⋅ S 1 ⋅ S 0 ‾ ⋅ D 6 + S 2 ⋅ S 1 ⋅ S 0 ⋅ D 7 Y=\overline{S_2}·\overline{S_1}·\overline{S_0}·D_0 +\overline{S_2}·\overline{S_1}·S_0·D_1 +\overline{S_2}·S_1·\overline{S_0}·D_2 +\overline{S_2}·S_1·S_0·D_3 +S_2·\overline{S_1}·\overline{S_0}·D_4 +S_2·\overline{S_1}·S_0·D_5 +S_2·S_1·\overline{S_0}·D_6 +S_2·S_1·S_0·D_7 Y=S2⋅S1⋅S0⋅D0+S2⋅S1⋅S0⋅D1+S2⋅S1⋅S0⋅D2+S2⋅S1⋅S0⋅D3+S2⋅S1⋅S0⋅D4+S2⋅S1⋅S0⋅D5+S2⋅S1⋅S0⋅D6+S2⋅S1⋅S0⋅D7 -
Y = m 0 ⋅ D 0 + m 1 ⋅ D 1 + m 2 ⋅ D 2 + m 3 ⋅ D 3 + m 4 ⋅ D 4 + m 5 ⋅ D 5 + m 6 ⋅ D 6 + m 7 ⋅ D 7 Y=m_0·D_0 +m_1·D_1 +m_2·D_2 +m_3·D_3 +m_4·D_4 +m_5·D_5 +m_6·D_6 +m_7·D_7 Y=m0⋅D0+m1⋅D1+m2⋅D2+m3⋅D3+m4⋅D4+m5⋅D5+m6⋅D6+m7⋅D7
-
逻辑函数 L = A ‾ B C + A B ‾ C + A B L=\overline{A}BC+A\overline{B}C+AB L=ABC+ABC+AB
L = A ‾ B C + A B ‾ C + A B = A ‾ B C + A B ‾ C + A B C ‾ + A B C = m 3 + m 5 + m 6 + m 7 L=\overline{A}BC+A\overline{B}C+AB=\overline{A}BC+A\overline{B}C+AB\overline{C}+ABC=m_3+m_5+m_6+m_7 L=ABC+ABC+AB=ABC+ABC+ABC+ABC=m3+m5+m6+m7 -
使用8选1数据选择器实现上述函数L
L = Y = m 3 + m 5 + m 6 + m 7 ,其中 D 7 D 6 D 5 D 3 = 1111 , D 4 D 2 D 1 D 0 = 0000 L=Y=m_3+m_5+m_6+m_7,其中D_7D_6D_5D_3=1111,D_4D_2D_1D_0=0000 L=Y=m3+m5+m6+m7,其中D7D6D5D3=1111,D4D2D1D0=0000

-
-
并行数据转串行数据

4.4.4 数值比较器
1. 定义和功能
- 对两个数的大小进行比较。
(1)1位数值比较器
- 列出真值表
| A | B | F A > B F_{A>B} FA>B | F A < B F_{A<B} FA<B | F A = = B F_{A==B} FA==B |
|---|---|---|---|---|
| 0 | 0 | 0 | 0 | 1 |
| 0 | 1 | 0 | 1 | 0 |
| 1 | 0 | 1 | 0 | 0 |
| 1 | 1 | 0 | 0 | 1 |
- 逻辑表达式
- F A > B = A ⋅ B ‾ F_{A>B} = A·\overline{B} FA>B=A⋅B
- F A < B = A ‾ ⋅ B F_{A<B} = \overline{A}·B FA<B=A⋅B
- F A = = B = A ⋅ B + A ‾ ⋅ B ‾ F_{A==B} = A·B+\overline{A}·\overline{B} FA==B=A⋅B+A⋅B
- 逻辑图

(2)2位数值比较器
- 列出真值表
| A 1 ? B 1 A _1?B_1 A1?B1 | A 0 ? B 0 A_0?B_0 A0?B0 | F A > B F_{A>B} FA>B | F A < B F_{A<B} FA<B | F A = = B F_{A==B} FA==B |
|---|---|---|---|---|
| A 1 > B 1 A_1>B_1 A1>B1 | x | 1 | 0 | 0 |
| A 1 < B 1 A_1<B_1 A1<B1 | x | 0 | 1 | 0 |
| A 1 = = B 1 A_1==B_1 A1==B1 | A 0 > B 0 A_0>B_0 A0>B0 | 1 | 0 | 0 |
| A 1 = = B 1 A_1==B_1 A1==B1 | A 0 < B 0 A_0<B_0 A0<B0 | 0 | 1 | 0 |
| A 1 = = B 1 A_1==B_1 A1==B1 | A 0 = = B 0 A_0==B_0 A0==B0 | 0 | 0 | 1 |
-
逻辑表达式
F A > B = F A 1 > B 1 + F A 1 = = B 1 ⋅ F A 0 > B 0 F_{A>B} = F_{A_1>B_1} +F_{A_1==B_1}·F_{A_0>B_0} FA>B=FA1>B1+FA1==B1⋅FA0>B0
F A < B = F A 1 < B 1 + F A 1 = = B 1 ⋅ F A 0 < B 0 F_{A<B} = F_{A_1<B_1} +F_{A_1==B_1}·F_{A_0<B_0} FA<B=FA1<B1+FA1==B1⋅FA0<B0
F A = = B = F A 1 = = B 1 ⋅ F A 0 = = B 0 F_{A==B} = F_{A_1==B_1}·F_{A_0==B_0} FA==B=FA1==B1⋅FA0==B0 -
逻辑图

2. 集成数值比较器
- 74x85,4位数值比较器。(CMOS型74HC85)
- 74x682,8位数值比较器。
(1)74HC85的功能
-
I
A
>
B
、
I
A
=
B
、
I
A
<
B
I_{A>B}、I_{A=B}、I_{A<B}
IA>B、IA=B、IA<B是扩展输入端。当4位输入AB都相等时,根据扩展输入端,判断AB的大小。

- 列出真值表即可写出逻辑表达式。
(2)数值比较器的位数扩展
-
串联,扩展为8位数值比较器

-
并联,扩展为16位数值比较器。
-
并联的当时,速度快。