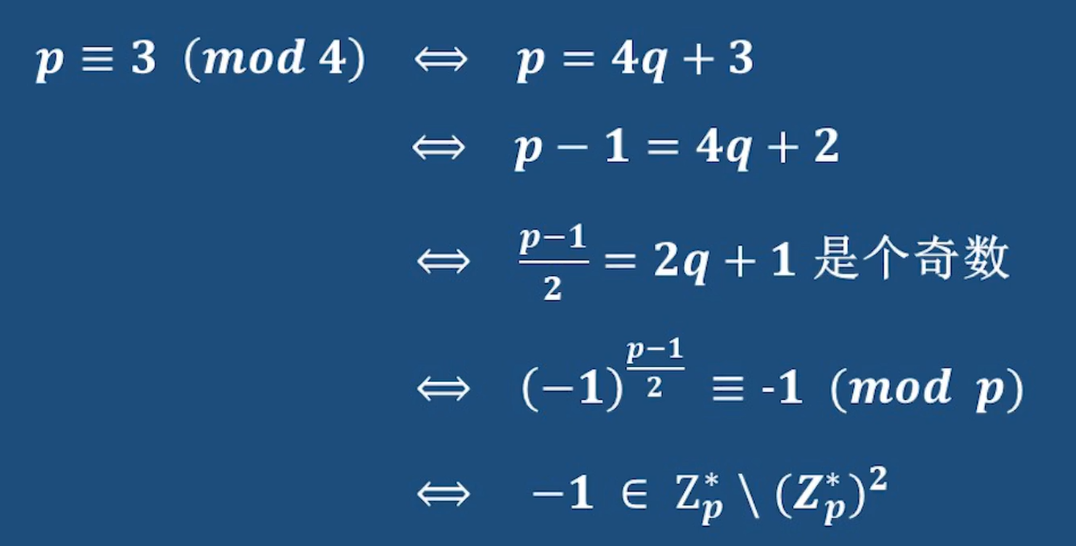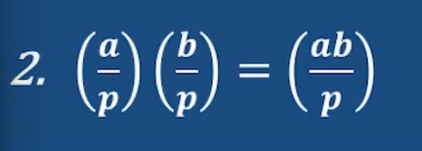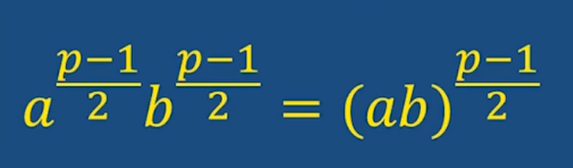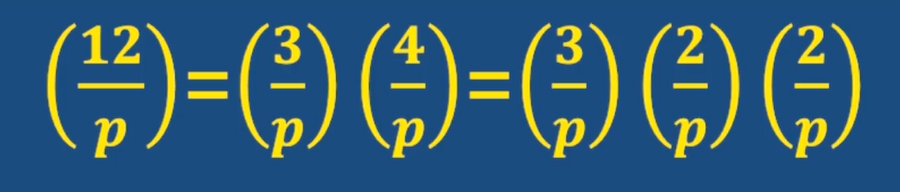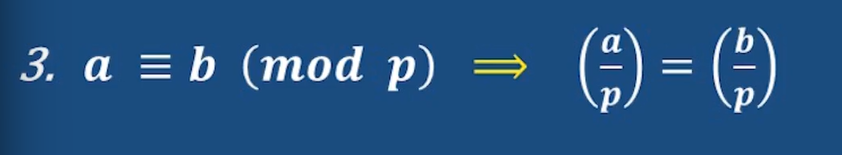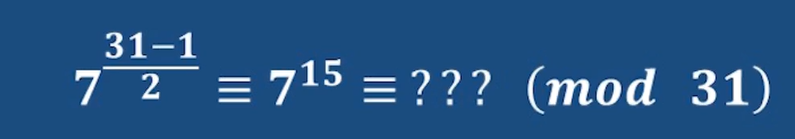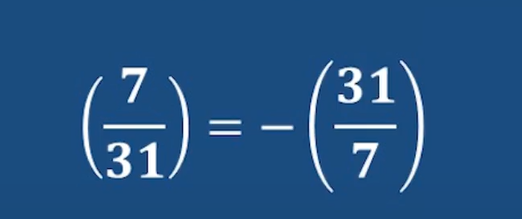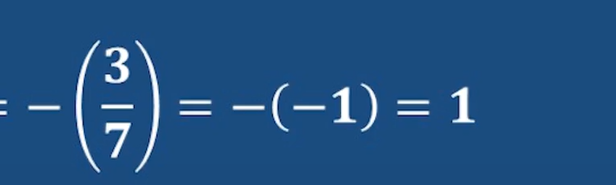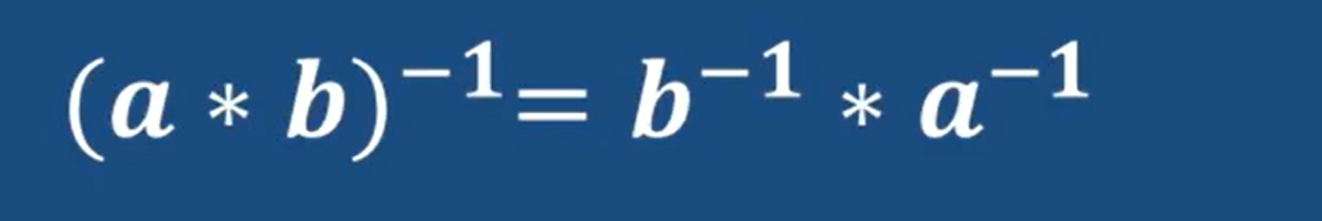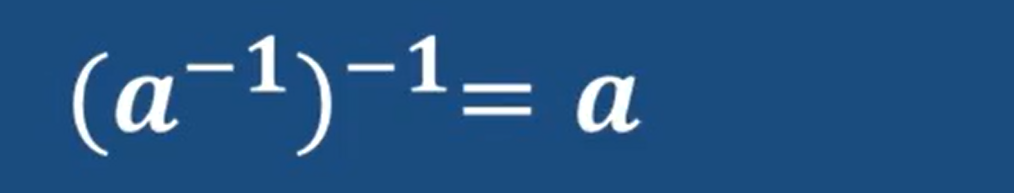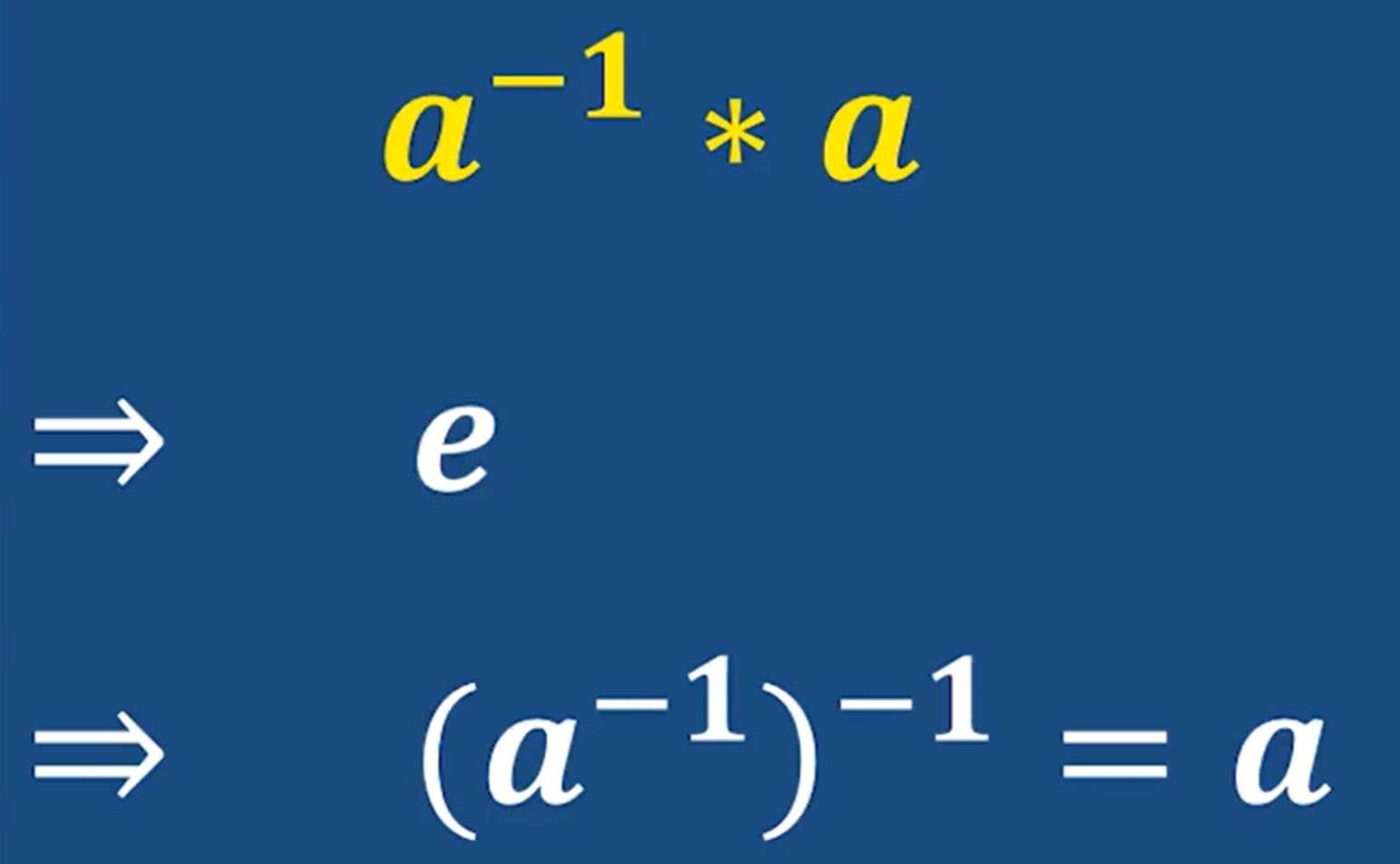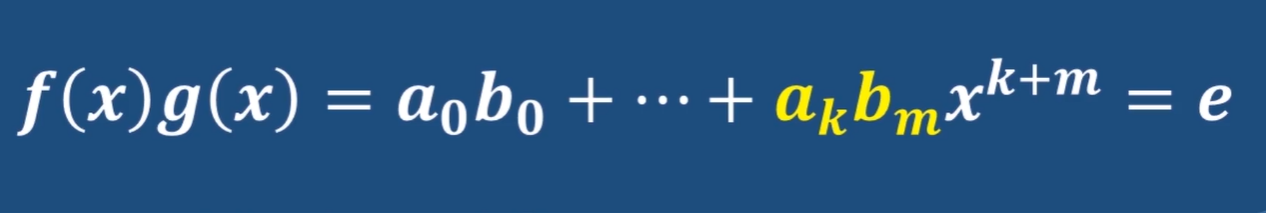【CTF-Crypto】数论基础-02
文章目录
- 【CTF-Crypto】数论基础-02
- 1-16 二次剩余
- 1-20 模p下-1的平方根*
- 1-21 Legendre符号*
- 1-22 Jacobi符号*
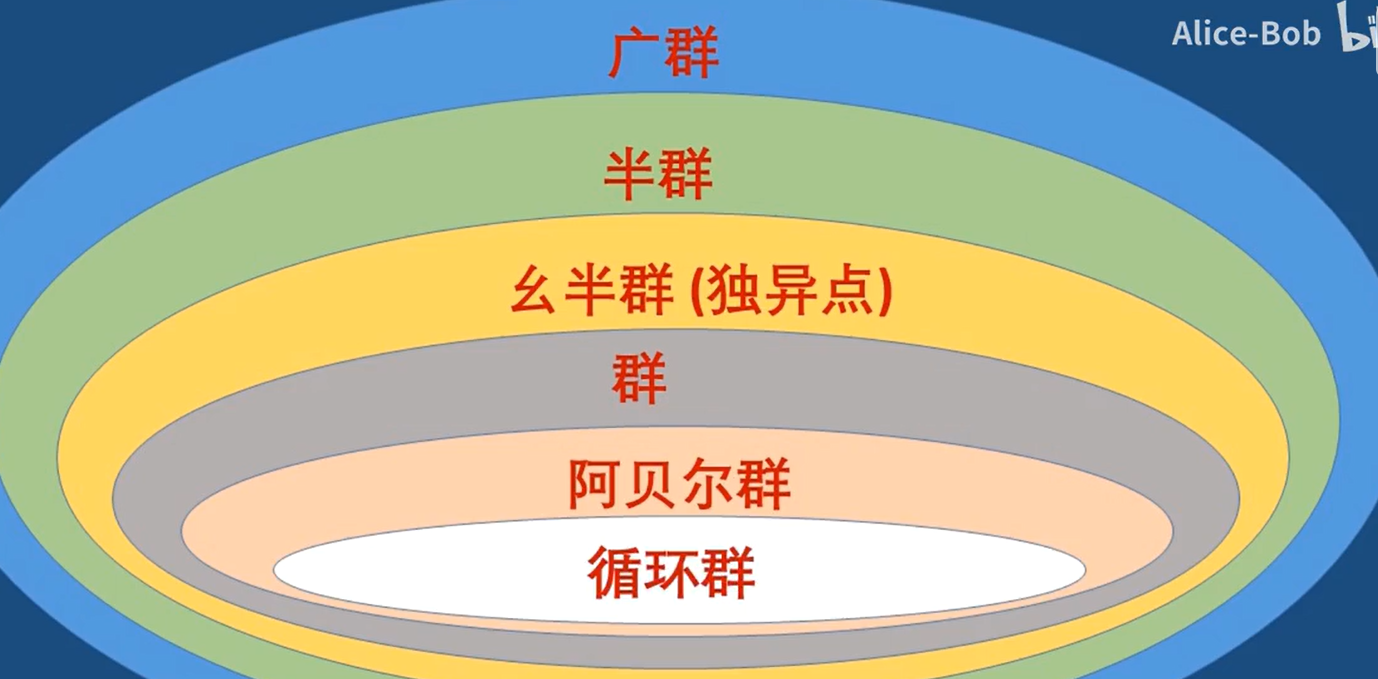
- 2-1 群*
- 2-2 群的性质
- 2-3 阿贝尔群*
- 2-4 子群
- 2-11 群同态
- 2-18 原根
- 2-21 什么是环
- 2-23 什么是域
- 2-25 子环
- 2-26 理想
- 2-32 多项式环
1-16 二次剩余
是什么?

定义:

判断是否有解的一个方法:把小于模数的全代入一遍,看看有没有解
如:
把x从1到6分别代入x,会发现方程都不成立
所以3不是模7下的二次剩余
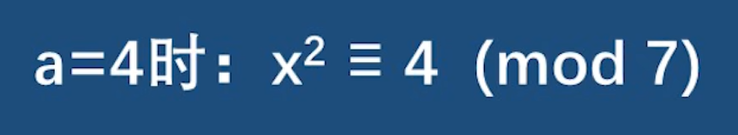
当a=4时, x从1到6尝试 可以发现2或5可以满足式子,所以4是模7下的二次剩余
下面进行正向推测,x从1到6 计算右边

所得结果有1、2、4 表明模7下二次剩余的是a = 1 2 4
问题一般化:模n下,什么样的整数a才是二次剩余(有平方根)?
首先明确一个二次剩余的集合

这个集合里面的元素就是模n下余数的平方 再模n的结果
故有 该集合里的任意整数a 必然存在整数b 使得b的平方和a模n下同余

从而得到二次剩余的判断方法

性质
二次剩余的性质和模数有非常密切的关系:
- 模p下的二次剩余
p是奇素数(p是素数,且p不等于2)
回顾:
这个例子刚讲过,模7下的二次剩余的a是1 2 4 一共三个 二次非剩余也是3个
同时关于平方根,也可以发现,1对应的平方根是1和6 4对应的平方根是2和5 2对应的平方根是3和4 每个对应的都是两个
以1为例,看他的两个平方根分别是1和6 因为是模7 所以6可以写成-1 因为-1+7 = 6
基于上面这个正负1的情况,在普通运算下没有任何问题,但是在模运算下需要推导证明

证明:

进而证明下面那个b和c的结论

这个结论告诉我们,如果a=b^2 则a恰有两个根 正负b
进一步推导,Zp星里的每个整数都可以做平方 其个数就是二次剩余的个数

这个上面也提到过,每个整数对应正负两个 其中负的那个可以转化一下
所以真正的个数是我们每次遍历的一半 也就是p-1的一半
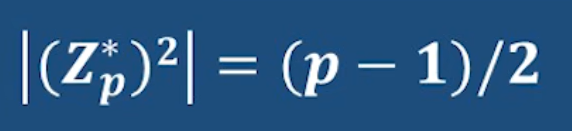
小重点:欧拉准则(二次剩余的判定定理)

第一条证明: 注意下面的式子 都是在模p下 才有等于1的这个结论

具体等于1还是-1 取决于第2条还是第3条 如果是二次剩余 就是1 如果是二次非剩余 就是-1
原因:
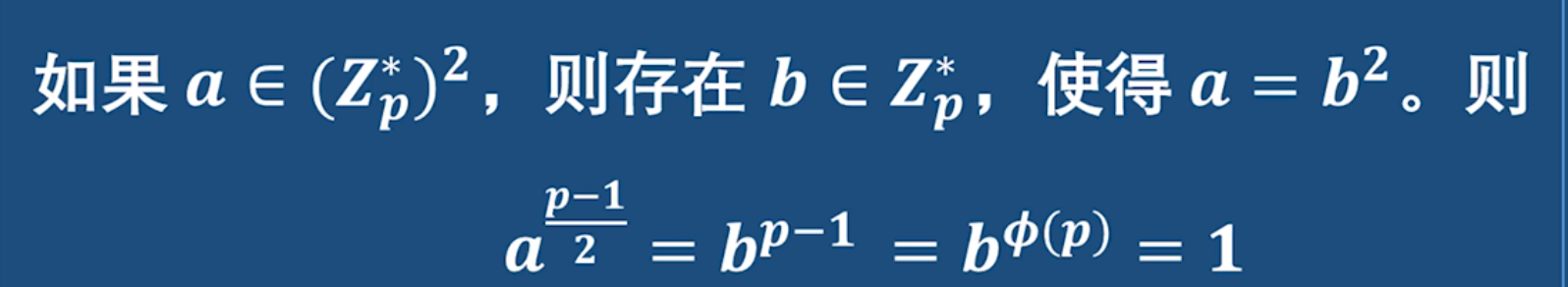
讨论两个整数在模p下相乘 所得积的情况
-
两个都相同类型的情况下 相乘结果一定是二次剩余

-
如果只有一个整数是二次非剩余 则结果是二次非剩余
计算方法:
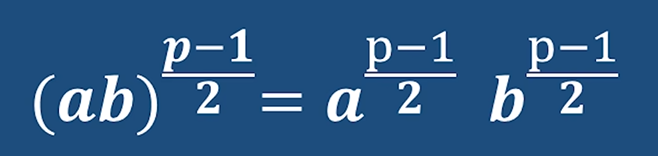
拆开 分别计算 套用欧拉准则
陷阱:如果告诉你两个数乘积是二次剩余 那么这两个数也是二次剩余 是错误的 因为有可能都是二次非剩余
常见性质 补充版

1-20 模p下-1的平方根*
- 引言:
下面的性质和余数是1的p有关,p是奇素数

- 如何判断-1是不是模p下的二次剩余
常规思路:对-1使用欧拉准则 看看结果是否等于1
利用性质的简单方法:
-

举例:

p % 13 = 14 % 13 = 1 所以根据性质1 得到-1是集合的自己,即-1是模13下的二次
使用欧拉准则证明一下
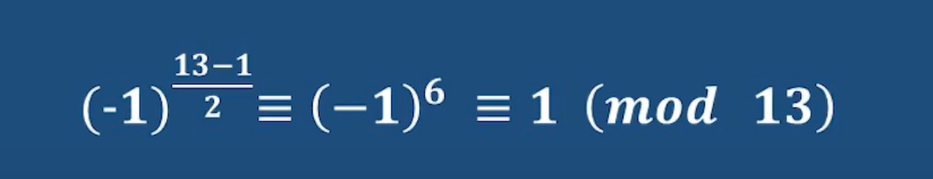
证明:

上面可以看出来 对-1使用欧拉准则所得结果必然是1,此时-1就是二次剩余
如果是这中情况 模4下和1同余,那么此时-1是二次非剩余
1-21 Legendre符号*
对于奇素数p,在模p下判断a是否是二次剩余
最直接的方法:
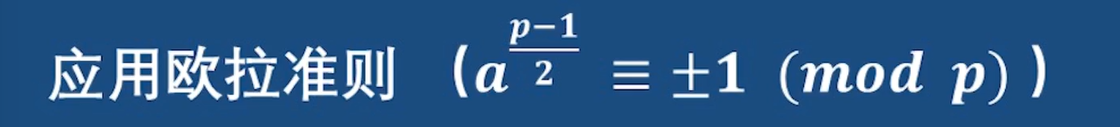
便捷方法:
只要发现p模4和1同余,那么-1就一定是模p下的二次剩余,而不需要对-1使用欧拉准则
但是可以发现上面的这个便捷判断只能针对-1进行判断,那么对于其他任意整数呢,如何判断呢,所以引出了Legendre符号

其中结果为1 表示a是模p的二次剩余
结果为-1 表示a是模p的二次非剩余
但是目前直接看这个好像没发现什么便捷性,其实利用该符号的一些性质,可以使得运算从指数级运算降低
性质1:欧拉准则和Legendre符号的等价转换关系
性质2:
证明:利用欧拉准则的形式
应用举例:
性质3:
因为a和b同余,那么这俩就必然同为二次剩余或同为二次非剩余,必然同时等于1或-1
性质4:
性质5:二次互反律(law of quadratic reciprocity)
特点:
反之为负的
当p等于q时 整除 根据Legendre符号 式子两边均为0 等式一定成立
使用方法:
例1:入门:
如果使用欧拉准则
非常麻烦,不好计算
既然7和31都是奇素数,可以应用Legendre符号+二次互反律
首先因为7和31模4都不等于1 所以根据二次互反律符号为负
然后31可以模7化简一下
剩下的可以试一试 或者 欧拉准则
例2:补充一下上面的应用事项
因为 17 和 31 均为奇素数,所以可以使用二次互反定律 此外因为 17 和 31 模 4 均不为一,所以根据 L e g e n d r e 符号,结果为 1 ( 17 31 ) = ( 31 17 ) 此时可以发现模数变小了,所以可以优化一下分子,令分子模 17 ( 14 17 ) 此时继续使用二次互反定律!发现是不行的,因为 14 不是奇素数 所以此时使用 L e g e n d r e 的性质,对其进行拆分 ( 14 17 ) = ( 2 17 ) ( 7 17 ) 看到 2 在分子上使用性质 4 ,得到结果为 1 所以最后只剩下 7 17 可以发现均是奇素数,所以可以使用二次互反定律缩小模数 7 17 = 17 7 = 3 7 继续,二次互换先判断是否有模 4 余 1 的奇素数,均没有则领金加符号 17 7 = 3 7 = − 7 3 = − 1 3 = − 1 \\~~~因为17和31均为奇素数,所以可以使用二次互反定律\\ 此外因为17和31模4均不为一,所以根据Legendre符号,结果为1\\ (\frac {17}{31}) =(\frac {31}{17}) \\ 此时可以发现模数变小了,所以可以优化一下分子,令分子模17\\ (\frac {14} {17})~~此时继续使用二次互反定律!发现是不行的,因为14不是奇素数\\ 所以此时使用Legendre的性质,对其进行拆分(\frac {14} {17})=(\frac{2}{17})(\frac{7}{17})\\ 看到2在分子上 使用性质4,得到结果为1 所以最后只剩下\frac {7}{17}\\ 可以发现均是奇素数,所以可以使用二次互反定律 缩小模数\\ \frac {7}{17} = \frac {17}{7} = \frac{3}{7} \\ 继续,二次互换 先判断是否有模4余1的奇素数,均没有 则领金 加符号 \frac {17}{7} = \frac{3}{7} =-\frac{7}{3}= -\frac{1}{3} = -1 因为17和31均为奇素数,所以可以使用二次互反定律此外因为17和31模4均不为一,所以根据Legendre符号,结果为1(3117)=(1731)此时可以发现模数变小了,所以可以优化一下分子,令分子模17(1714) 此时继续使用二次互反定律!发现是不行的,因为14不是奇素数所以此时使用Legendre的性质,对其进行拆分(1714)=(172)(177)看到2在分子上使用性质4,得到结果为1所以最后只剩下177可以发现均是奇素数,所以可以使用二次互反定律缩小模数177=717=73继续,二次互换先判断是否有模4余1的奇素数,均没有则领金加符号717=73=−37=−31=−1
1-22 Jacobi符号*
其实不要把这个符号想的太陌生,其实就是Legendre符号的推广演化而来

可以发现对分子分母的条件减少了一些限定
注意奇素数p可以彼此相同,这样右边的式子就是Legendre符号

当a和n不互素时 结果为0
一些性质 非常类似:

性质5:如果模数是合数,则可以把合数拆分 然后分别计算
作用:可以直接把一些大模数化成一些小模数,而且不用关心负号问题
二次互反律的推广


雅可比符号判断二次剩余性



第三个表示 如果a是模n下的二次剩余,则雅可比符号为1
推导:
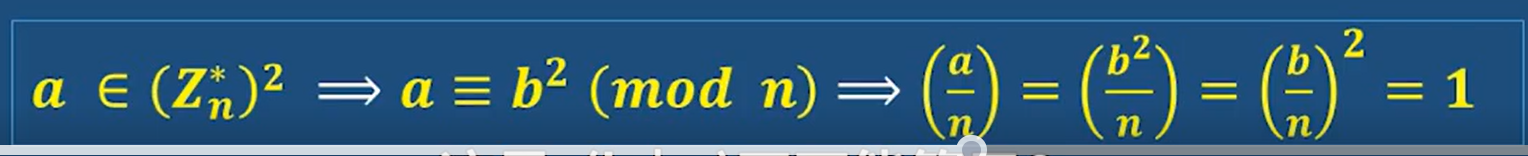
2-1 群*
体系:
代数结构
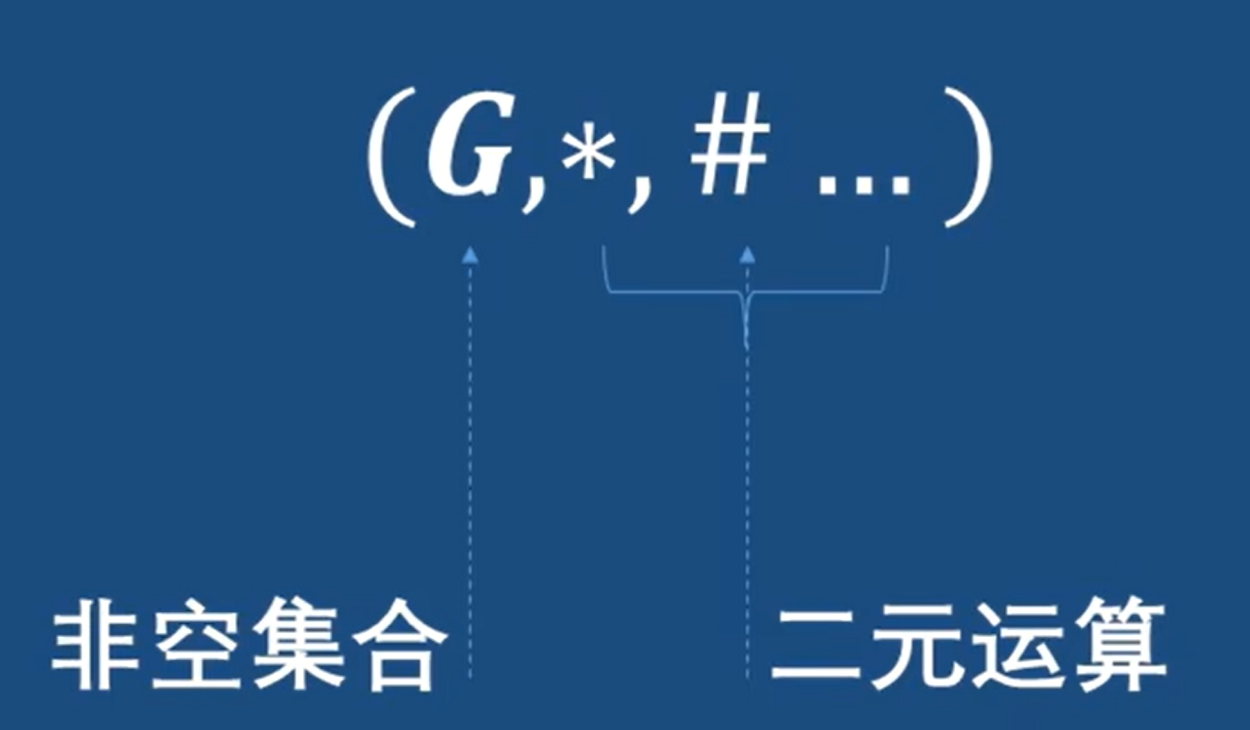
- 封闭性
集合里任意两个元素的二元运算的结果,是跑不出这个集合的
反例

这样就不能说自己是代数结构
关于群(group)需要满足下面四个性质:

在一个群中,因为逆元的存在,出现了逆运算
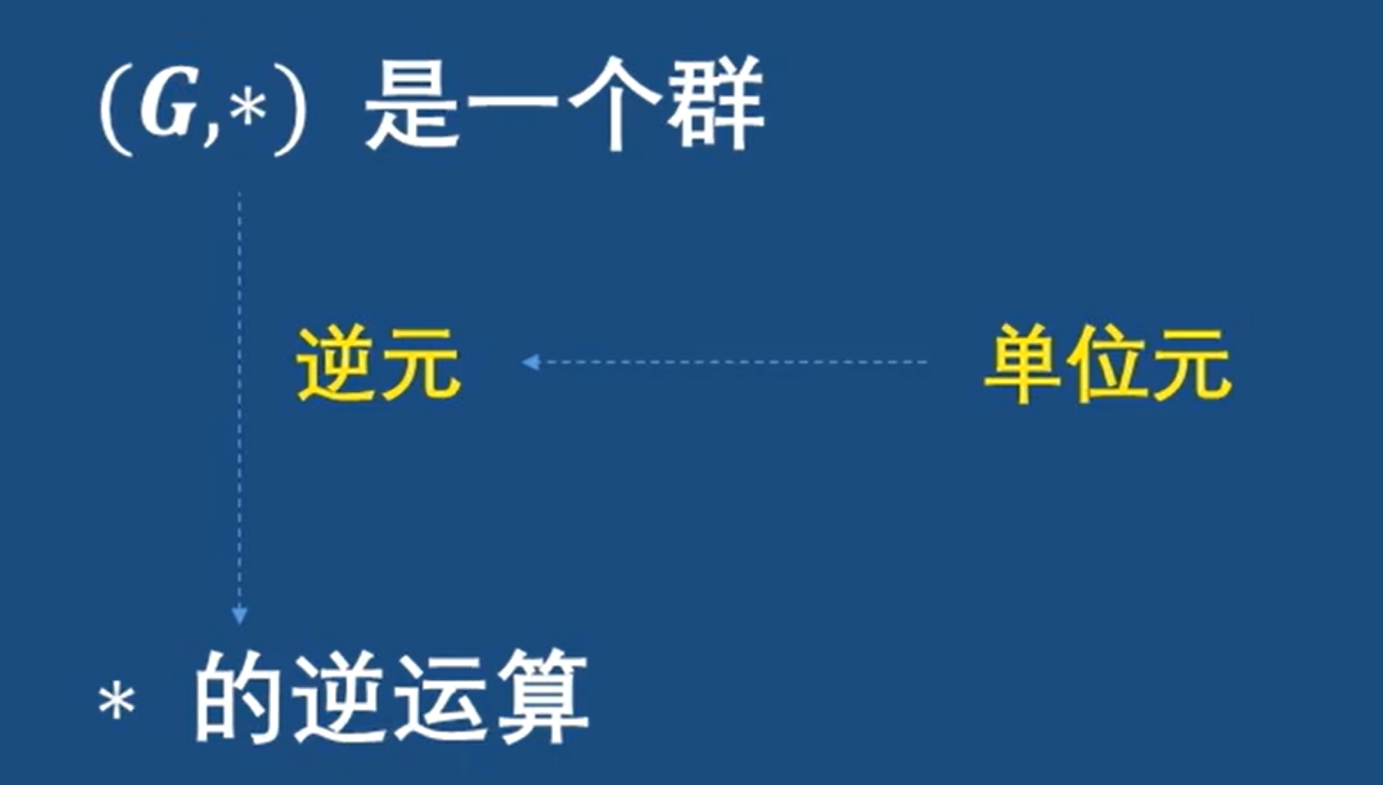
判断是不是群,就看是否满足上面四个性质
举例:
-

-
不是群,

因为有0的存在 修正

- 模运算的例子

小tip:

2-2 群的性质
-
分类:
- 有限群:

- 无限群:

-
定理1 : 群里的单位元是唯一的

计算过程根据单位元的性质,和单位元的运算还等于本身
- 定理2 : 每个元素只有唯一的逆元

注意啊 可能有些元素以自身为逆元
- 平凡群

- 群的性质:
- 消去律
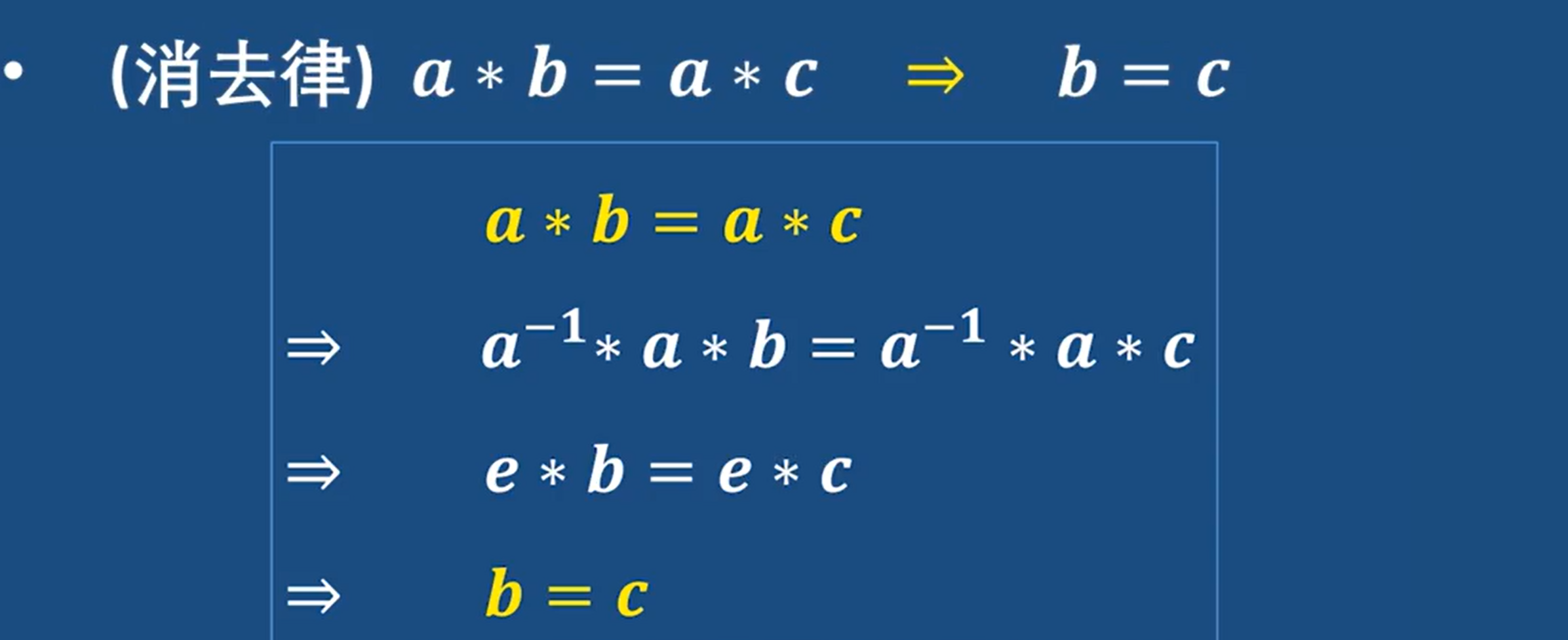
- 方程解

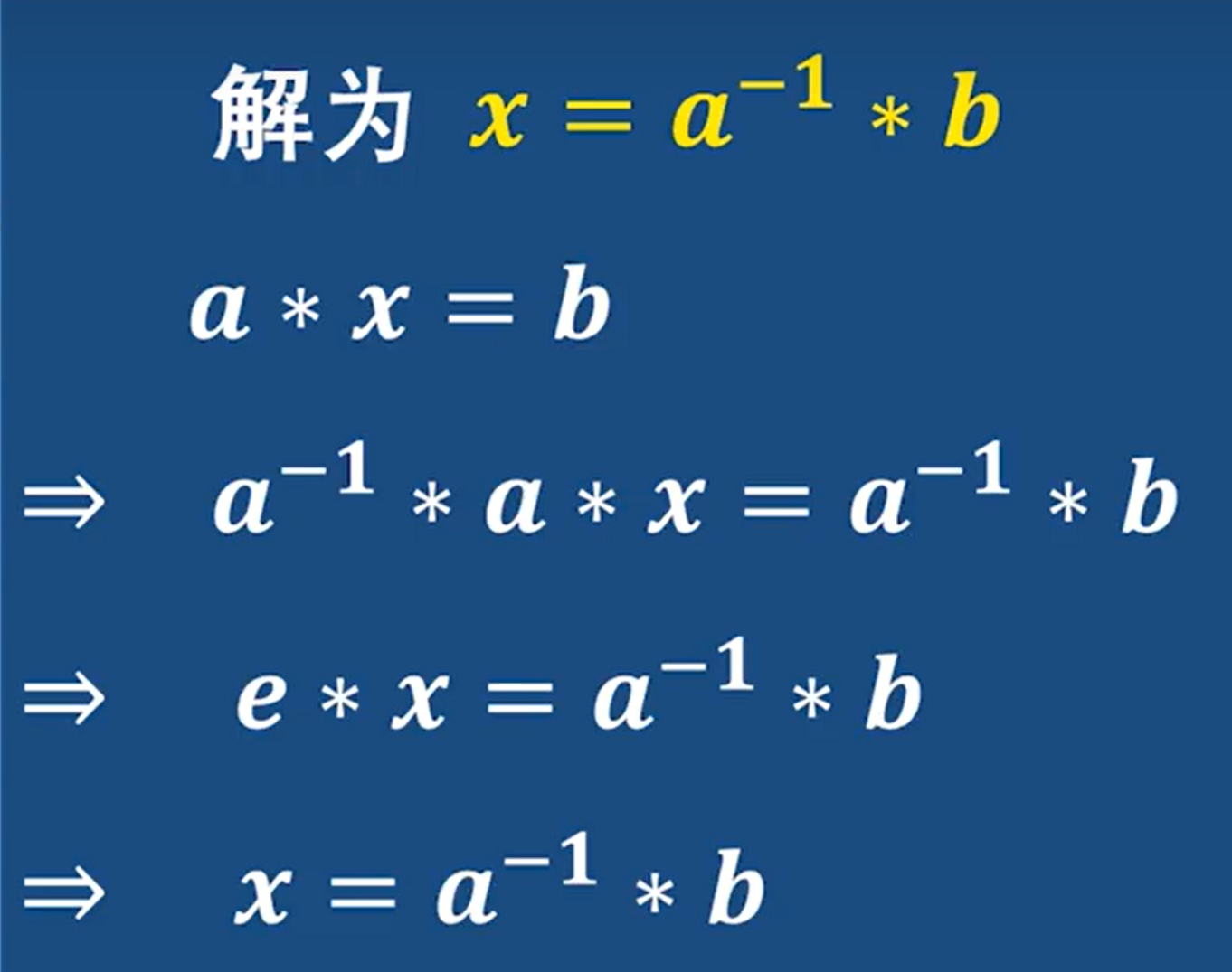
注意:群里的运算不一定满足交换律 所以左右位置还是有区别的
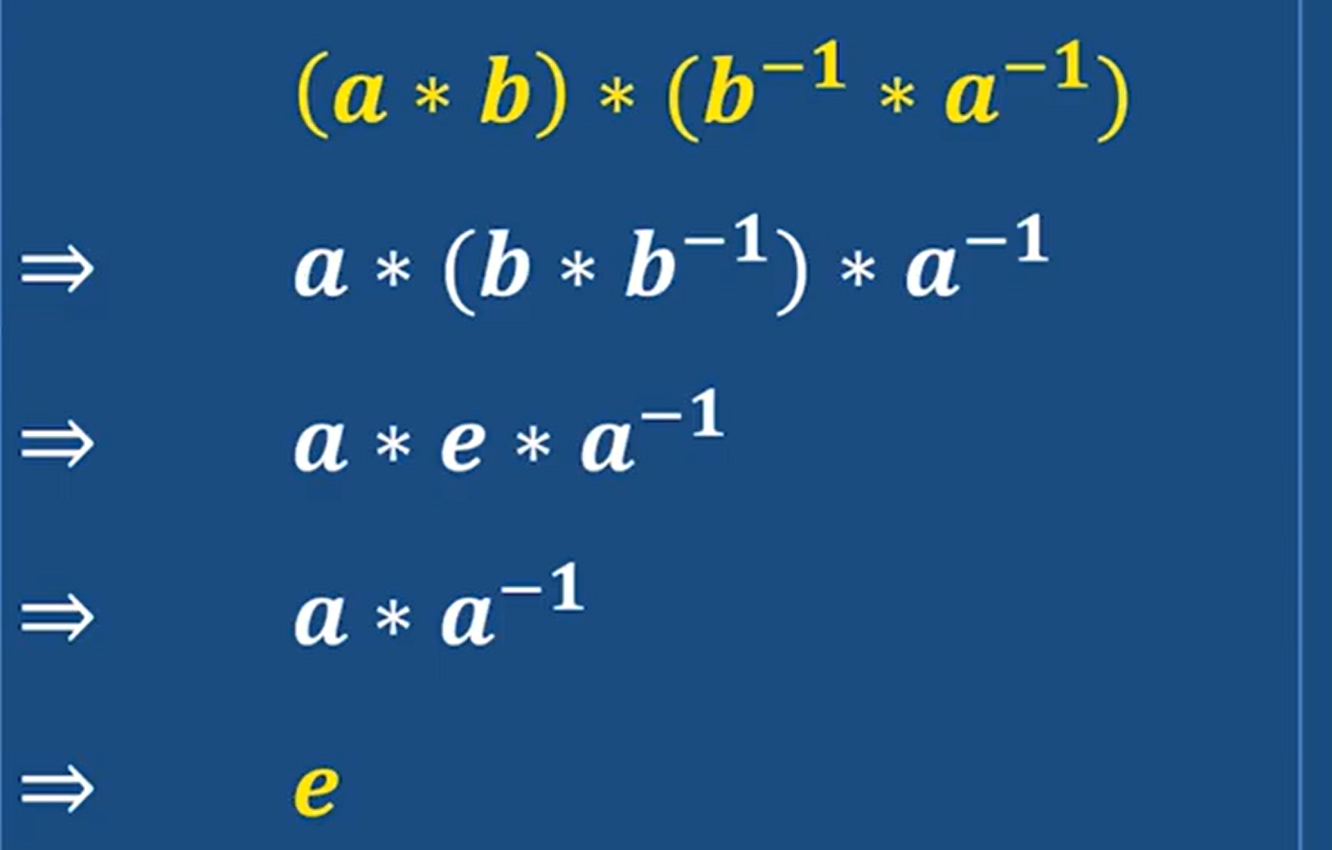
因为a的逆元和a相乘是单位元e 所以a的逆元 和a 互为逆元
2-3 阿贝尔群*
在群的基础上,多出来一个性质,当运算满足交换律时,则称为阿贝尔群,也称交换群

从群到阿贝尔群,如何快速证明

定理证明:


利用消去律
简记方法:
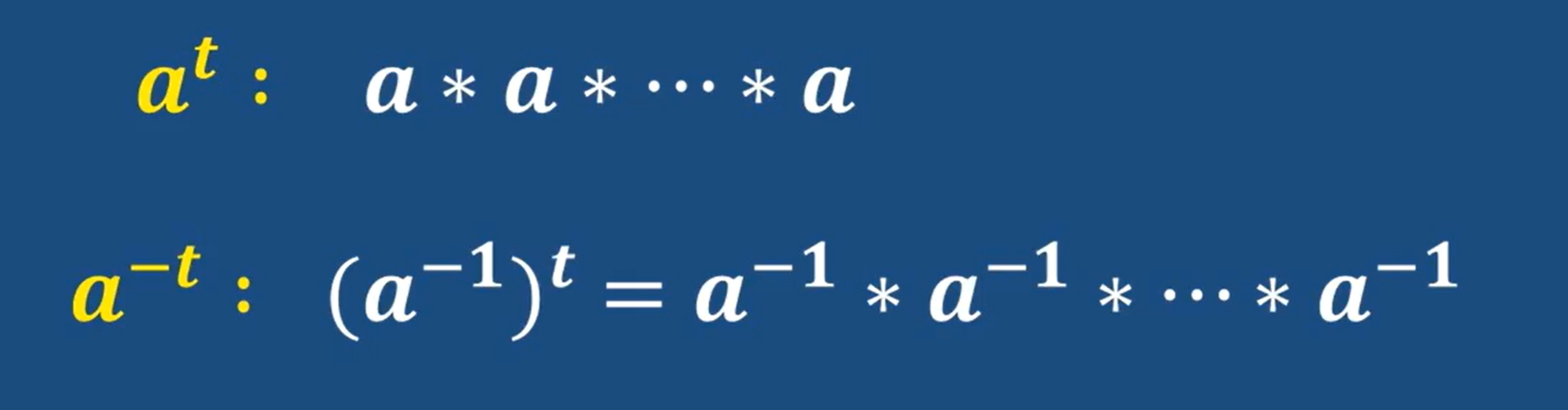
注意这里的次方运算,表示多少个元素做相同运算,符号由群定义,不是单独的乘方运算
推广

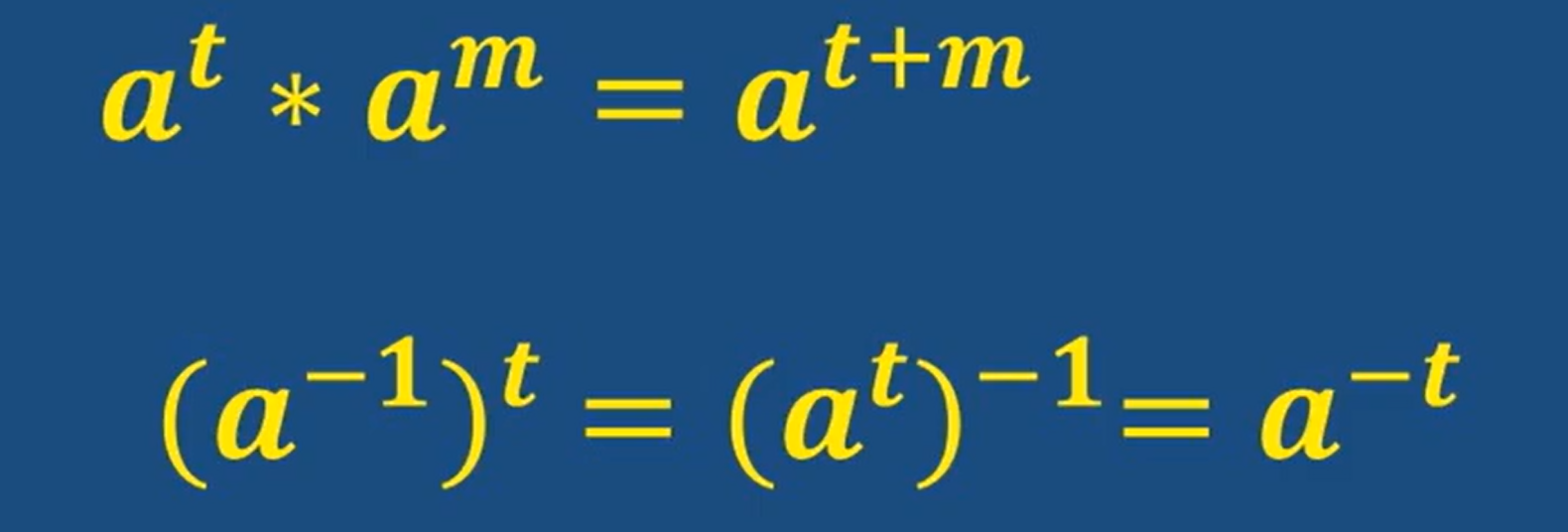
上面这个的证明:证明是逆元关系

来个定理

2-4 子群
定义:

G的子群分类:
-
平凡子群:

-
非平凡子群:

定理:
- 群的单位元也是其子群的单位元

-
元素在子群中,其逆元也必在该子群中

有人问,有没有可能
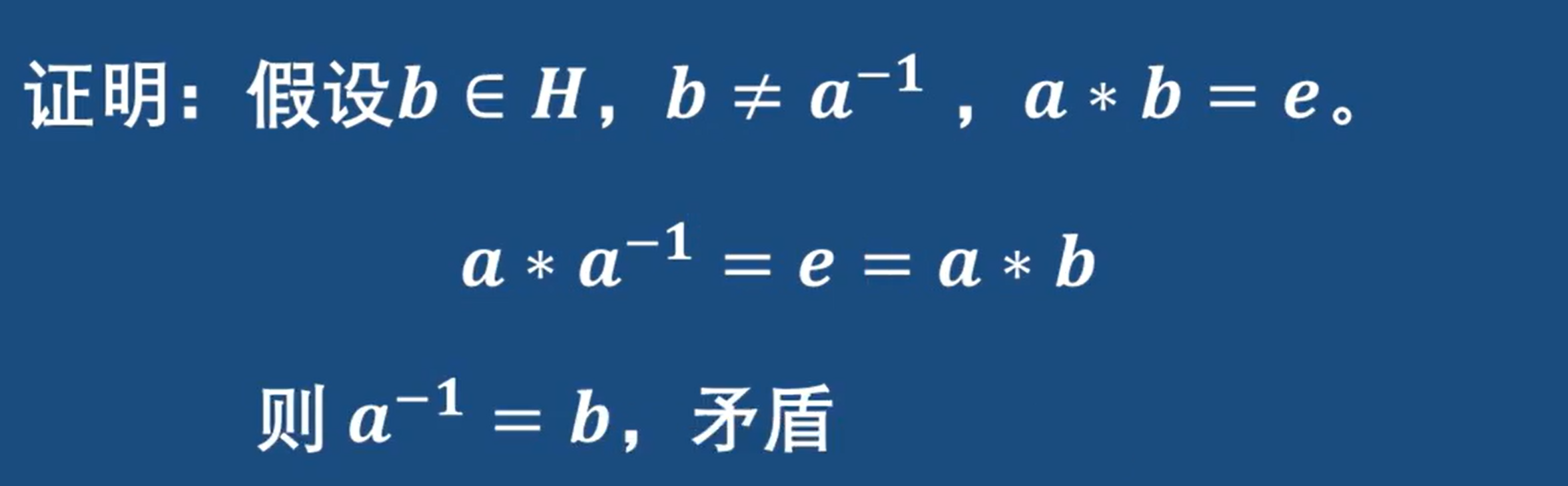
如何判断子群
方法一:

先证明单位元:式子里a和b可以相等

证明逆元:令a = 单位元e b = a 套用式子

证明封闭性:
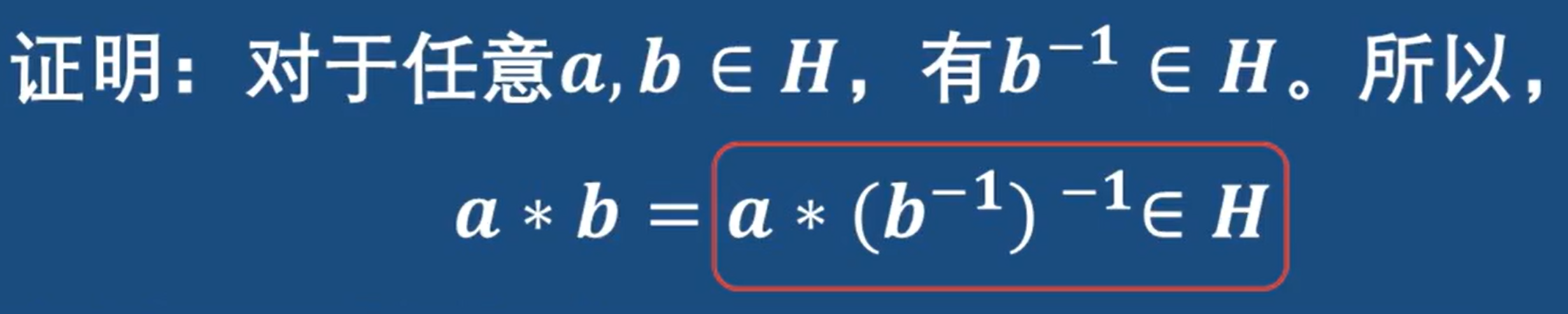
红框里面在利用式子,b的逆作为式子里的b,得出a和b进行二元运算是属于H的 结果封闭
结合律:因为G是群 对于其元素 必然满足结合律
方法2:

2-11 群同态
基本定义

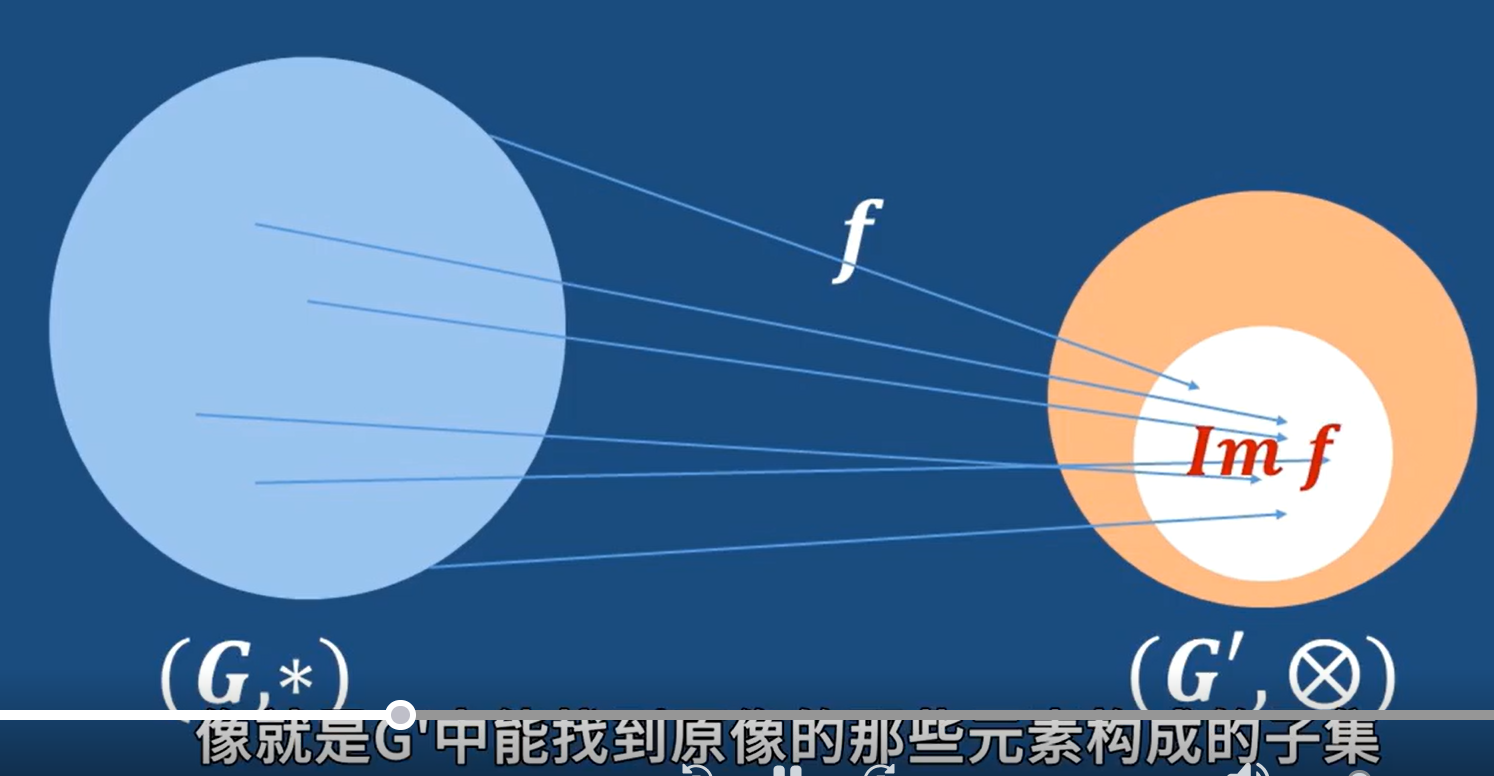
图示:

两个特殊子集:
- 同态像
- 同态核:
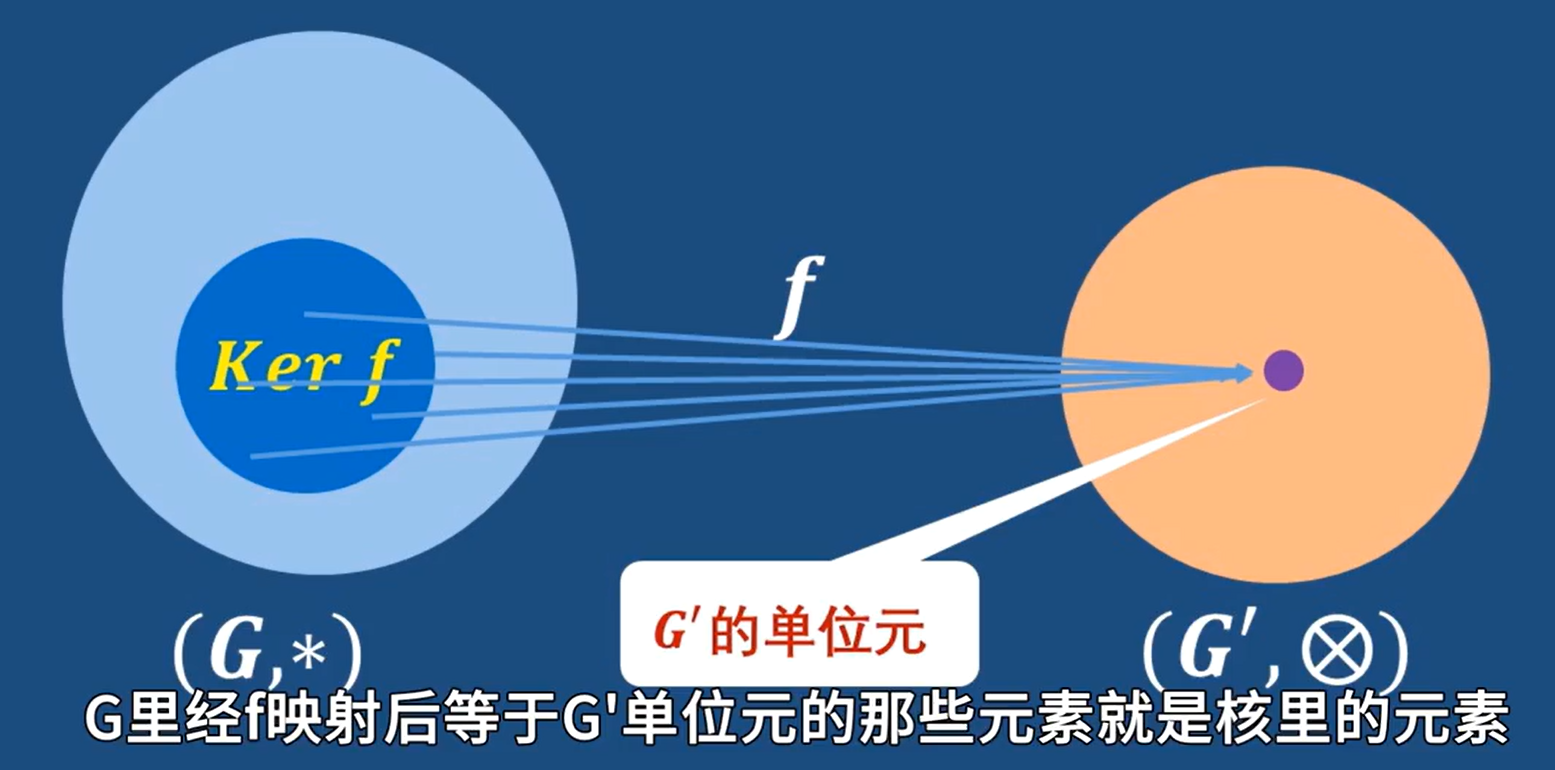
符号表示:

- 嵌入映射
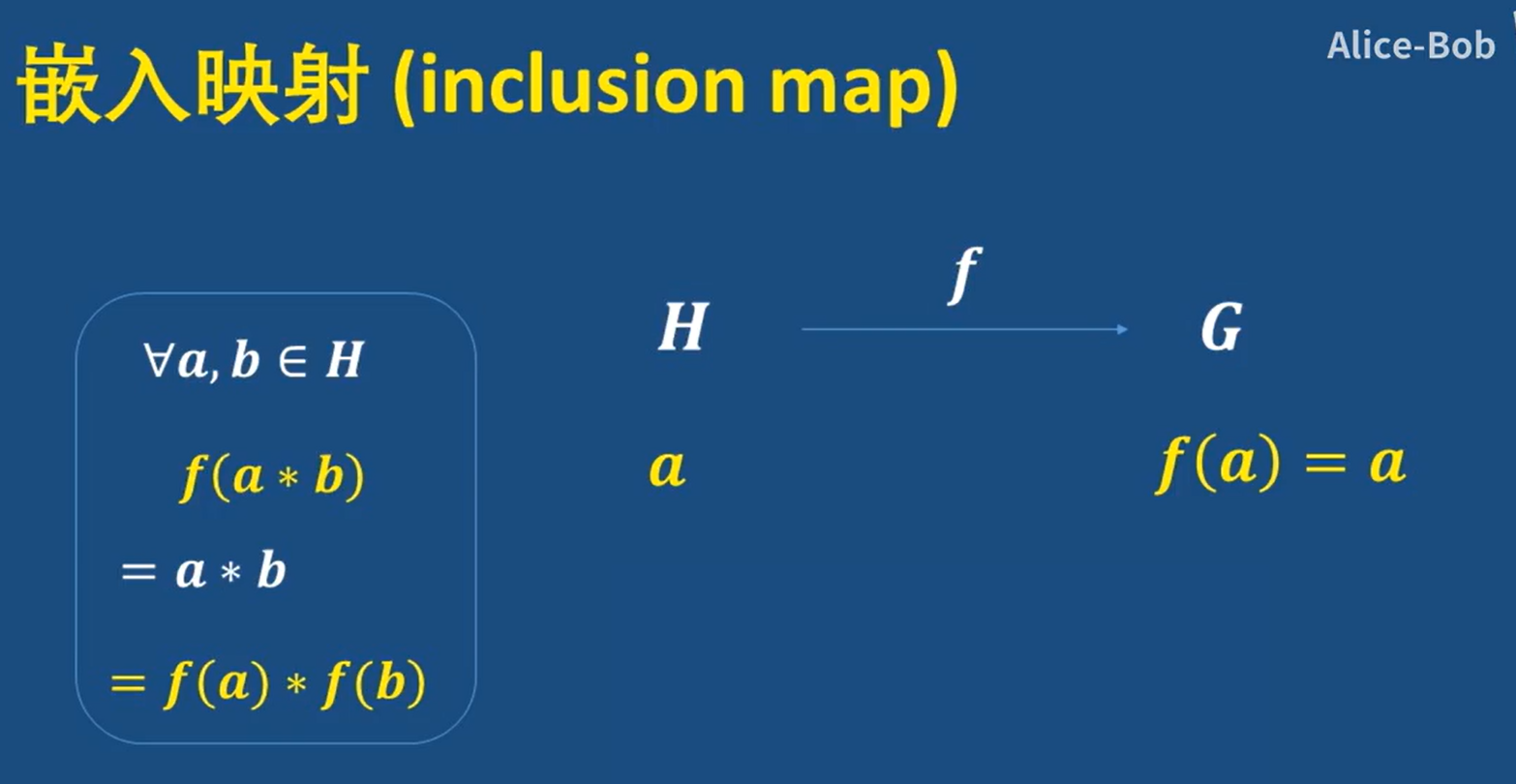
其中H是G的子集,这就相当于是子群到群的映射,并且原像到像之间是一一对应的,所以这是一个单射,也可以叫作单一同态
- 自然映射
N是G的正规子群
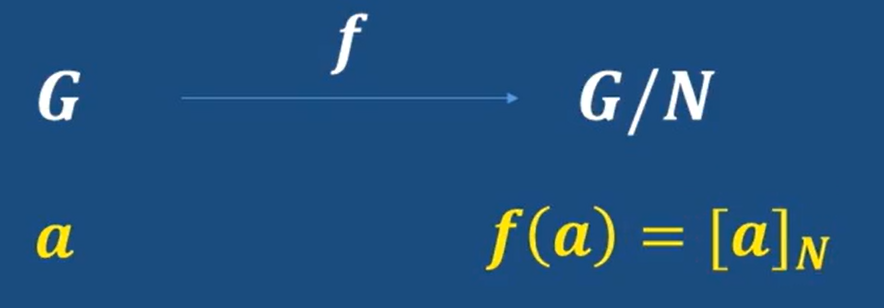
每个元素a会通过函数映射到相应的陪集

-
m次方映射
-
雅可比映射
几个性质:利用一个群的知识去分析另一个群
- 单位元穿越后仍然是单位元
理论证明:

- 逆元穿越后仍然互为逆元

理论证明:
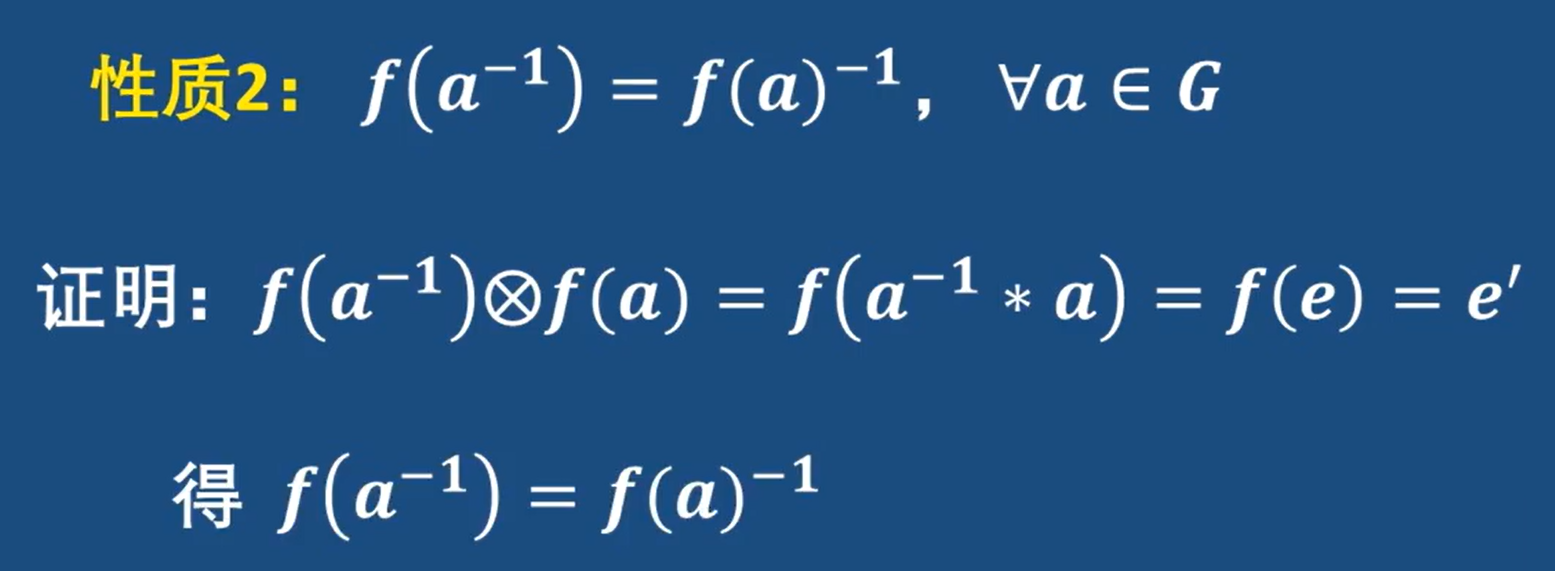
- 子群
理论证明:
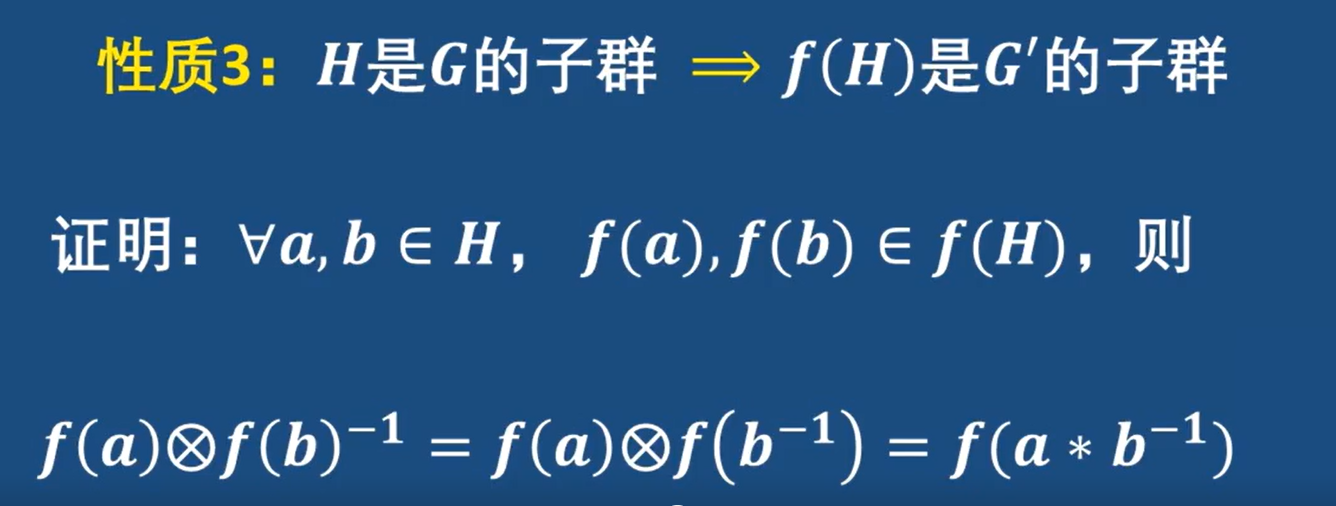
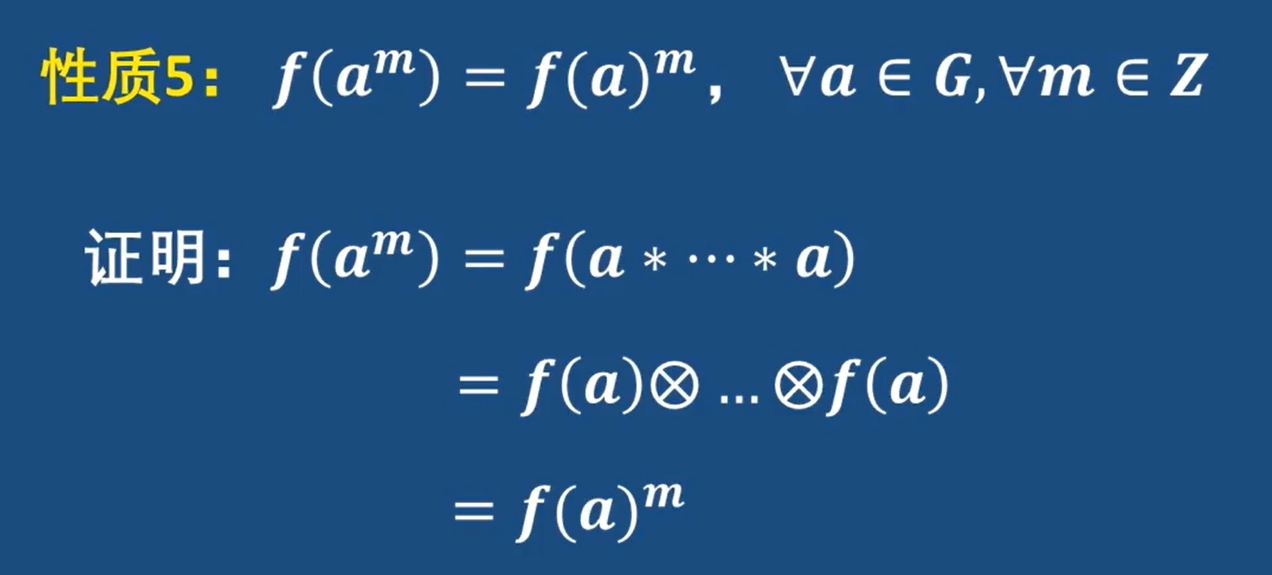
2-18 原根

“原根”存在的条件:(因为模n下并不一定有原根)

只有当n满足上面这五种情况之一 才会存在原根
举个反例:RSA算法,其模数n是两个大素数的乘积,所以不存在原根
一些性质:

Zn*中的元素为phin个 所以其阶也就是phin
这样原根的阶和Zn*的阶相同,这样原根就可以生成Zn* 的所有元素


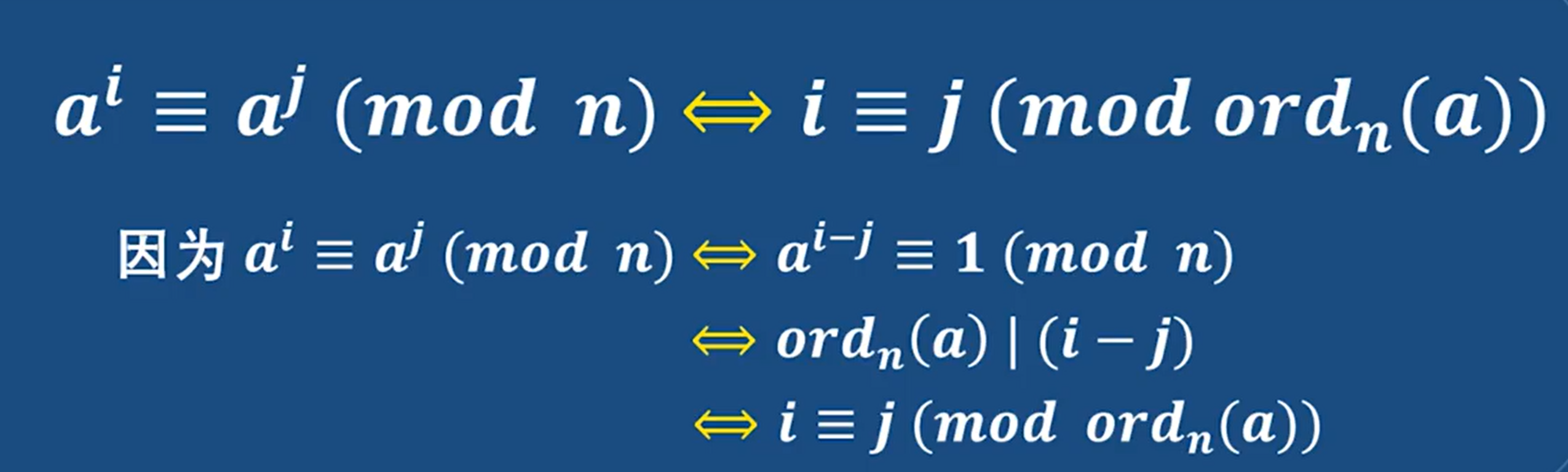










如何找原根:
方法:
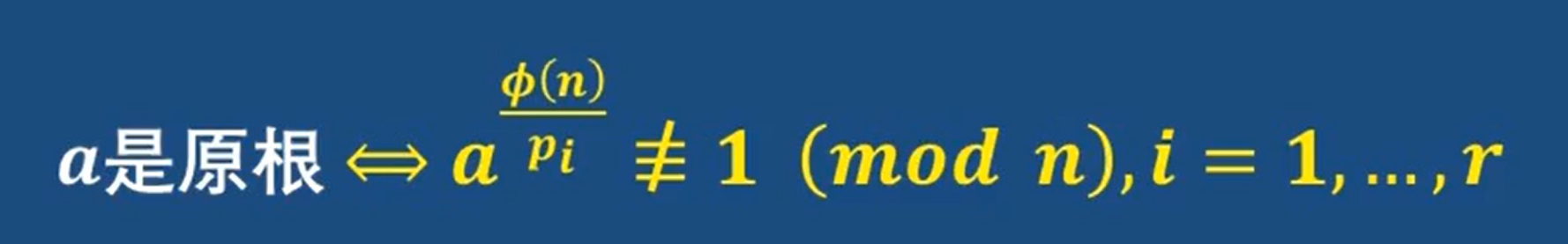

举个例子:

这样可以得知 2是模19下的原根
2-21 什么是环
代数结构:
和群不同的是,这里有两个二元运算符号,注意这里的加法和乘法都是抽象概念,不是真正的加减
环的定义:


分类:
- 有限环:环的元素数量是有限的
- 无限环:环的元素数量是无限的
举例:



一些符号表示

尤其关注一下加法逆元的表示为负数
运算性质:

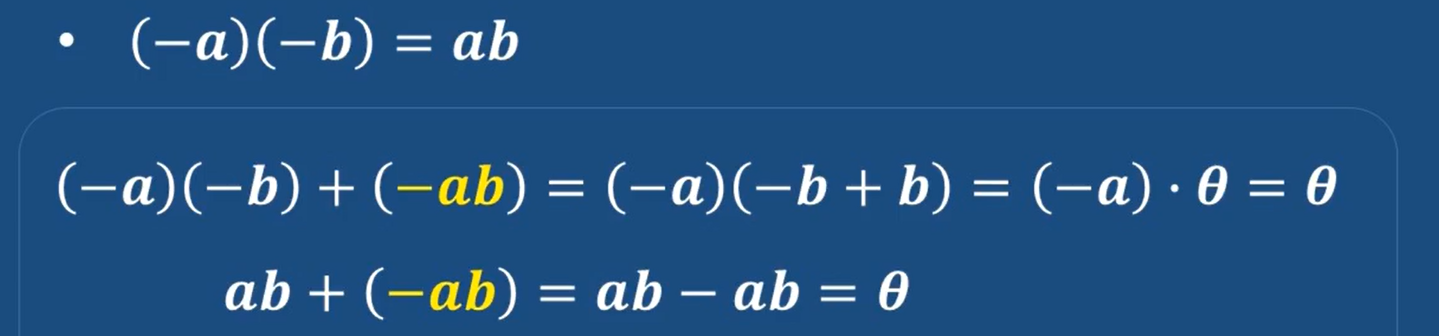

2-23 什么是域
继承环,引出一下域
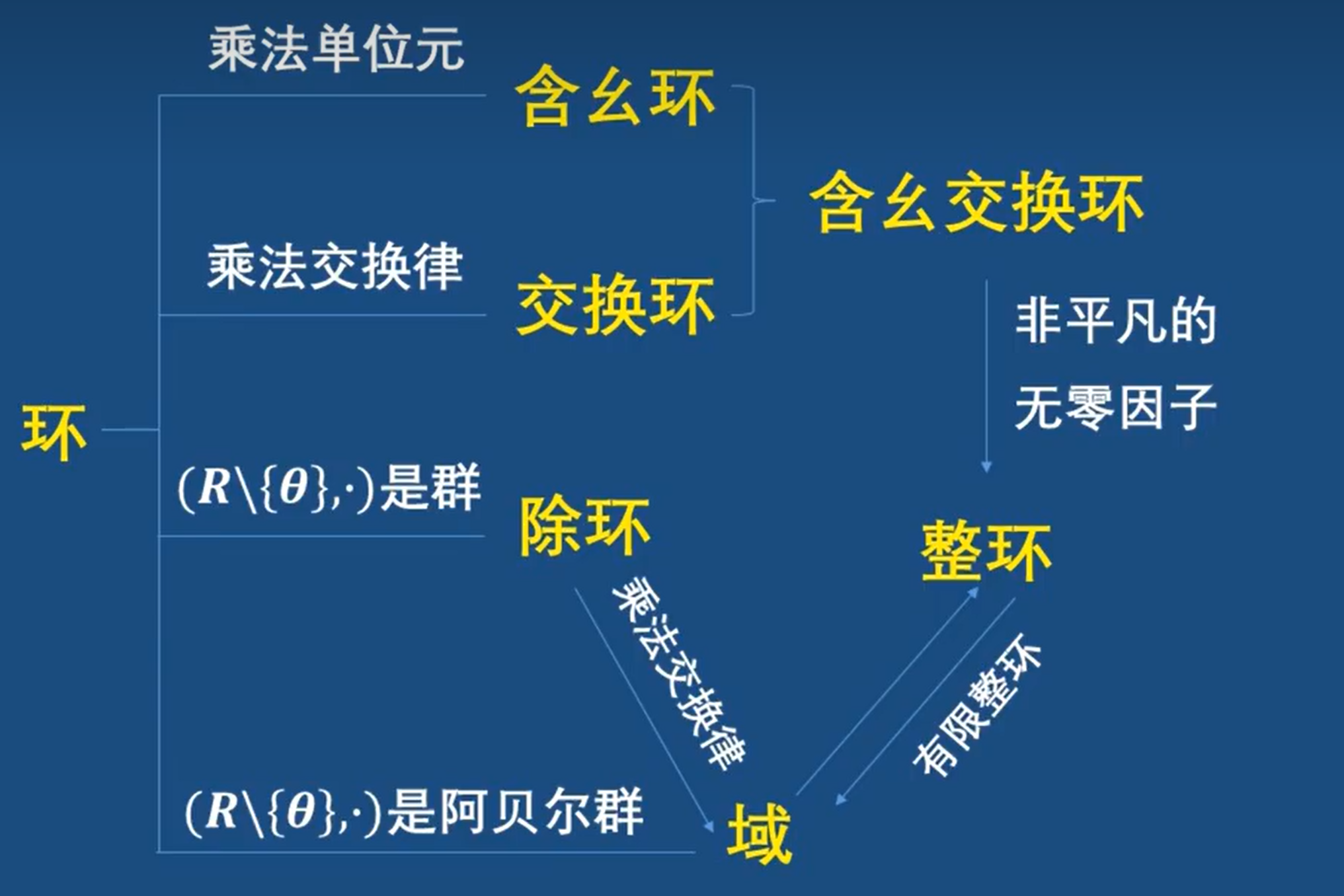
域的定义

整环和域的对比
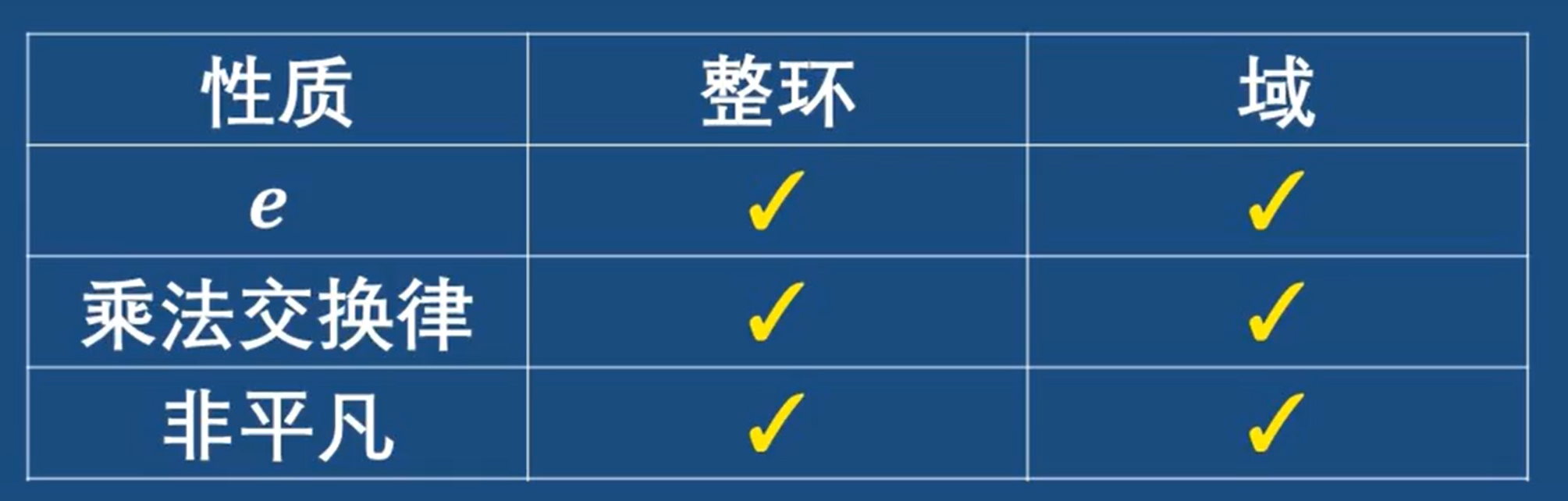
解释一下域的非平凡原因:
因为域有加法和乘法两个群,作为环的一种,域必然有零元
而非零元素要形成乘法阿贝尔群,那非零元素这部分就不能是空集
也就是说除了零元以外,域必然有其他元素,故域是非平凡的




2-25 子环
子环的定义:(类似群和子群的定义

特殊性质:

举例:


mZ和Z在相同的运算下构成环,mZ里的整数都是Z的倍数,是Z的非空子集
特殊点:

Zn的元素其实都是剩余类,而不是整数,和Z里的并不是同一种东西;其中的运算也不同,Zn的是剩余类之间的运算,而Z则是普通的乘法和加法
如何判断是不是子环?
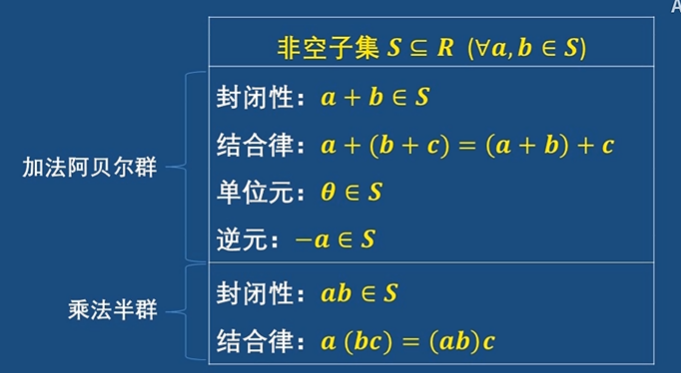
核心原则:只要非空子集在环的运算下构成阿贝尔群和半群即可
注意:
-
分配律不需要考虑,因为环满足分配律,它的非空子集必然也满足
-
乘法结合律也不用考虑,既然环满足,其非空子集必然也满足
-
加法的结合律也不用考虑
综上,可以得到一种简化版本的判断方法,如下:

其实关于零元也可以再简化,因为其他条件中已经暗含

即为:

但是利用子群的判断可以进一步简化,最简方法
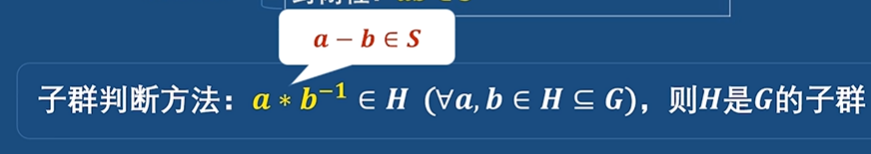



扩充:

举例:

注意事项:


非平凡的例子:

2-26 理想
介绍一下理想的本质:是一种特殊类型的子环

定义:

如何判断是不是理想:

简化逆元

关于定理:
为什么理想是子环

举例:


不断碰撞服务社会,占领了整个姐的底盘。
注意点:


都有单位元,都是矩阵,但是单位元不同
补充简单概念:

2-32 多项式环
类比学习:初中学的多项式建立在实数的基础上,几个单项式的和叫做多项式
在任意环上都可以建立多项式,这也是环比群强大的一个具体表现,因为多项式需要两种运算,而群只有一种
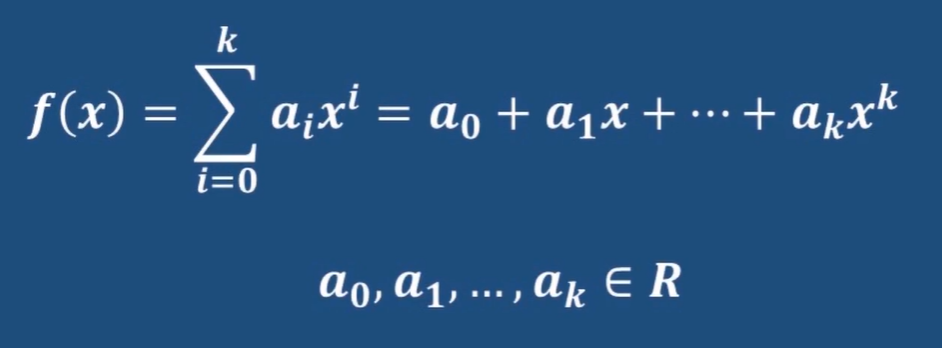
这里面a是多项式的系数,k是非负整数,叫多项式的度;变量x称为环上的不定元,也就是变量
当系数为零元时,相应的单项式可以省略不写;当系数为单位元e时,相应的单项式可以不写系数了
- 多项式环 定义:

基础加法和乘法运算和初中实数多项式类似
但是需要注意:
因为环不一定满足乘法交换律

- 常数多项式

关于度的性质:

- 其他性质

证明:
证明不是域 反证法
大学的思维对待