蓝桥杯重点（C/C++）（随时更新，更新时间：2023.2.2）

news2024/11/17 16:32:32

点关注不迷路，欢迎推荐给更多人，大约两天更新一次，建议点赞收藏加关注

本次更新内容：1.STL部分详细讲述，放到一篇新的文章中

                         2. 部分细节优化

目录

1  技巧

1.1  取消同步（节约时间，甚至能多骗点分，最好每个程序都写上）

1.2  万能库（可能会耽误编译时间，但是省脑子）

1.3  蓝桥杯return 0千万别忘了写！！

1.4  编译设置（Dev C++）

1.5  memset填充函数

1.6  时间复杂度

1.6.1  常数阶  O（1）

1.6.2  对数阶  O（logn）

1.6.3  线性阶  O（n）

1.6.4  线性对数阶  O(nlogn)

1.6.5  多重循环  O（n^k）

1.7  剪枝

1.8  find函数

1.9 PI问题

1.10  C/C++帮助文档

1.11  最大空间

1.11.1  占用字节大小

1.11.2  常用数据范围

1.12  指针存字符串（了解）

2  算法+数据结构

2.1  BFS（宽度优先搜索）

2.2  DFS（深度优先搜索）

2.3  最大公约数和最小公倍数

2.4  进制转换+超大数据处理

2.4.1  十进制为媒介（常用型）

2.4.2  二进制为媒介（技巧型）（含超大数据处理）

2.5  二进制表示法

2.6  背包问题

2.6.1  01背包问题

2.6.2  多重背包问题（每种物品有多件）

2.6.3  完全背包问题（每种物品有无数件）

2.7  动态规划（DP）

2.8  贪心

2.9  分治（以后更新）

2.10  数字分拆到数组中

2.11  数字和字符串的互化

2.12  排序

2.13  冒泡排序法和二分查找法（最常用）

2.14  图论

2.15  常用树

2.16  快速幂算法

2.17  素数（质数）

2.17.1  暴力法

2.17.2  线性筛

2.18  递归

2.19  STL

1  技巧

1.1  取消同步（节约时间，甚至能多骗点分，最好每个程序都写上）

ios::sync_with_stdio(false);
	cin.tie(0);
	cout.tie(0);

1.2  万能库（可能会耽误编译时间，但是省脑子）

#include <bits/stdc++.h>

1.3  蓝桥杯return 0千万别忘了写！！

1.4  编译设置（Dev C++）

（1）工具->编译选项->编译器->编译时加入以下命令->调成C99

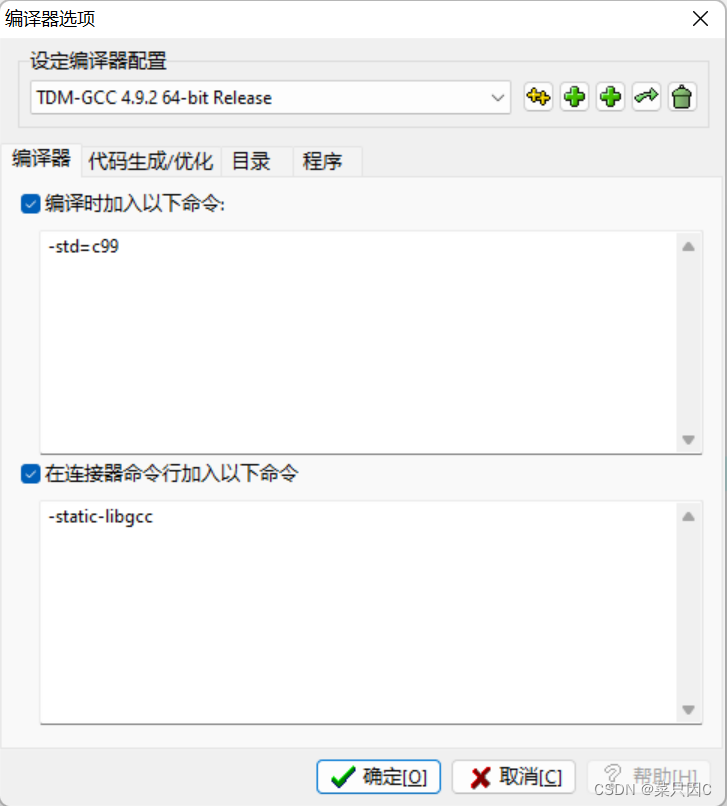
 （2）工具->编译选项->代码生成/优化->代码生成->语言标准

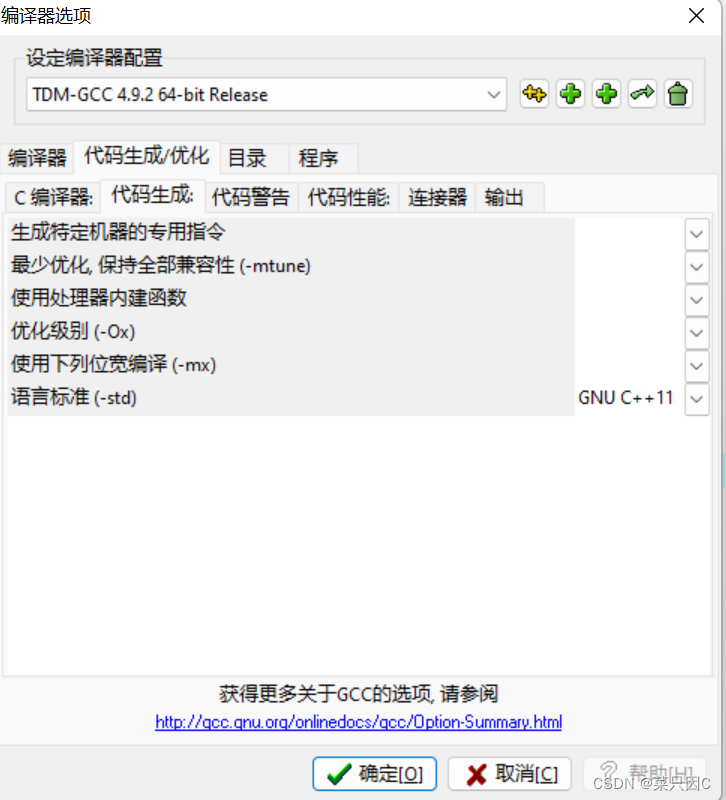
1.5  memset填充函数

按照字节对内存块进行初始化，注意只能填充0或-1

#include <bits/stdc++.h>
using namespace std;
int a[10];
int main()
{
	memset(a,-1,sizeof(a));
	for(int i=0;i<10;i++)
	{
		cout<<a[i]<<endl;
	}
	return 0;
}

1.6  时间复杂度

蓝桥杯每一道题编译时间都限制在1s以内，遇到数据比较大的题目，往往需要降低时间复杂度。

粗略估计，O（n）情况下一秒大概完成4亿次，O（n*n）情况下一秒大概完成2万次，O（n*n*n）情况下大概完成700次。

由于蓝桥杯评测系统是根据通过样例数来评分，所以我们做题时一定要注意约定样例取值范围。

例题：K倍区间（暴力法只能通过部分样例，所以要用更好的算法）

(1条消息) K倍区间（蓝桥杯2017年第八届省赛B组第十题）（C/C++）_菜只因C的博客-CSDN博客https://blog.csdn.net/m0_71934846/article/details/128434135?spm=1001.2014.3001.5501

1.6.1  常数阶  O（1）

int i=1;
int j=2;
int m=i+j;

1.6.2  对数阶  O（logn）

int i=1;
while(i<n)
{
  i=i*2;
}

1.6.3  线性阶  O（n）

for(int i=0;i<n;i++)
{
  cout<<i<<endl;
)

1.6.4  线性对数阶  O(nlogn)

for(int m=1;m<n;m++)
{
  int i=1;
  while(i<n)
  {
    i=i*2;
  }
}

1.6.5  多重循环  O（n^k）

k为循环层数

1.7  剪枝

做题时已经发现的不可能取到的数值，就不要再让计算机算了，尽量节省时间，蓝桥杯中目前遇到的还没有用到过过于繁琐的剪枝，大多也是在BFS和DFS中出现(bool vis)

1.8  find函数

函数作用：查找该元素在数组中第一次出现的位置的地址（类似于0x的地址）

模型：find（查找起点，查找终点，查找目标元素）

同样，查找区间为[查找起点，查找终点）

#include <bits/stdc++.h>
using namespace std;

int main()
{
	int a[10]={2,6,8,1,3,7,5,1,0,11};
	cout<<find(a+0,a+5,8)<<endl;//打印类似0x地址 
	cout<<find(a+0,a+5,8)-a<<endl;//打印数组【】内的序号 
	return 0;
}

1.9  PI问题

PI=atan（1.0）*4

PI=3.14159265

1.10  C/C++帮助文档

 

1.11  最大空间

1.11.1  占用字节大小

类型32位计算机64位计算机
char11
short int22
int44
long int48
long long int88
char*48
float44
double88

1.11.2  常用数据范围

类型范围估计值
char-128~+127
short-32767~+327683*10^4
unsigned short0~+655366*10^4
int=long-2147483648~+21474836472*10^9
unsigned int0~+42949672954*10^9
long long -9223372036854775808~+92233720368547758079*10^18

1.12  指针存字符串（了解）

这个比赛很少用指针，如果想要存储字符串，用指针也是一个不错的选择（直接可以用string类避免用指针）

//指针数组存储字符串列表
#include <stdio.h>
const int max = 5;
int main()
{
 const char *names[] = 
{  //定义指针数组，存储字符串列表
 "Zhang San",     //每个元素都是双引号括起来的
 "Li Si",
 "Wang Wu",
 "Su Wukong",
 "Tang Er",
 };
 
 int i=0;
 for(i=0;i<max;i++)
{
  printf("Value of names[%d] = %s\n",i,names[i]); // 注意 %s
 }
 return 0;
}

2  算法+数据结构

2.1  BFS（宽度优先搜索）

用到队列（有时会用到优先队列）

主要思想：把所有符合条件的点都压入队列，然后挨个元素弹出上下左右前后搜索，直到队列清空时代表搜索完毕，搜索的时候注意判断是否已经搜索过，用bool vis【】判断。

例题：全球变暖

(1条消息) 全球变暖（蓝桥杯2018年省赛B组试题I）（C/C++）_菜只因C的博客-CSDN博客https://blog.csdn.net/m0_71934846/article/details/128434254?spm=1001.2014.3001.5502

2.2  DFS（深度优先搜索）

用到递归（不好理解）

主要模板：可参见如下全排列例题

http://t.csdn.cn/ANnS1

总结起来有如下几步：

（1）确定 边界    if（）return；

（2）进入for循环

（3）判断是否搜索过  if（vis[]）vis[]=true; dfs();  vis[]=false;

例题1：凑算式

(3条消息) 凑算式（蓝桥杯2016年省赛B组第三题）（C/C++）_菜只因C的博客-CSDN博客https://blog.csdn.net/m0_71934846/article/details/128434004?spm=1001.2014.3001.5502

例题2:2n皇后问题

2n皇后问题（蓝桥杯基础练习C/C++）_菜只因C的博客-CSDN博客https://blog.csdn.net/m0_71934846/article/details/128772257?spm=1001.2014.3001.5501

2.3  最大公约数和最小公倍数

最大公约数（greatest common divisor，gcd）

#include <bits/stdc++.h>
using namespace std;

int main()
{
	cout<<__gcd(25,5);
	return 0;
}

最小公倍数 （least common multiple,lcm）

多写一个lcm函数

#include <bits/stdc++.h>
using namespace std;

int lcm(int a,int b)
{
    return a*b/__gcd(a,b);
}
int main()
{
	cout<<lcm(25,5);
	return 0;
}

2.4  进制转换+超大数据处理

2.4.1  十进制为媒介（常用型）

(8条消息) 任意进制转换成十进制/十进制转换成任意进制（ASCII码法）（C/C++）_菜只因C的博客-CSDN博客https://blog.csdn.net/m0_71934846/article/details/128297645?spm=1001.2014.3001.5502

2.4.2  二进制为媒介（技巧型）（含超大数据处理）

十六进制转八进制+超大数据处理（蓝桥杯基础练习C/C++）_菜只因C的博客-CSDN博客十六进制转八进制+超大数据处理（蓝桥杯基础练习C/C++）https://blog.csdn.net/m0_71934846/article/details/128745875?spm=1001.2014.3001.5502

2.5  二进制表示法

例题：无聊的逗

(8条消息) 蓝桥杯试题 算法训练 无聊的逗（C/C++）_菜只因C的博客-CSDN博客https://blog.csdn.net/m0_71934846/article/details/128717938?spm=1001.2014.3001.5502

2.6  背包问题

2.6.1  01背包问题

#include<bits/stdc++.h>

using namespace std;

int v[1000];    // 体积
int w[1000];    // 价值 
int f[1000][1000];  // f[i][j], j体积下前i个物品的最大价值 

int main() 
{
    int n, m;   
    cin >> n >> m;
    for(int i = 1; i <= n; i++) 
        cin >> v[i] >> w[i];

    for(int i = 1; i <= n; i++) 
        for(int j = 1; j <= m; j++)
        {
            //  当前背包容量装不进第i个物品，则价值等于前i-1个物品
            if(j < v[i]) 
                f[i][j] = f[i - 1][j];
            // 能装，需进行决策是否选择第i个物品
            else    
                f[i][j] = max(f[i - 1][j], f[i - 1][j - v[i]] + w[i]);
        }           

    cout << f[n][m] << endl;

    return 0;
}

2.6.2  多重背包问题（每种物品有多件）

把多件物品捏合成一件新的物品，按序号往后叠加即可

2.6.3  完全背包问题（每种物品有无数件）

#include<iostream>
using namespace std;
const int N = 1010;
int f[N];
int v[N],w[N];
int main()
{
    int n,m;
    cin>>n>>m;
    for(int i = 1 ; i <= n ;i ++)
    {
        cin>>v[i]>>w[i];
    }
 
    for(int i = 1 ; i<=n ;i++)
    for(int j = v[i] ; j<=m ;j++)
    {
            f[j] = max(f[j],f[j-v[i]]+w[i]);
    }
    cout<<f[m]<<endl;
}

2.7  动态规划（DP）

例题1：拿金币

(1条消息) 拿金币（蓝桥杯算法训练）（C/C++)_菜只因C的博客-CSDN博客https://blog.csdn.net/m0_71934846/article/details/128456365?spm=1001.2014.3001.5502

例题2：包子凑数

包子凑数（蓝桥杯2017年省赛B组试题H）（C/C++）_菜只因C的博客-CSDN博客包子凑数（蓝桥杯2017年省赛B组试题H）（C/C++）https://blog.csdn.net/m0_71934846/article/details/128434225?csdn_share_tail=%7B%22type%22%3A%22blog%22%2C%22rType%22%3A%22article%22%2C%22rId%22%3A%22128434225%22%2C%22source%22%3A%22m0_71934846%22%7D

2.8  贪心

思路：选取局部最优解，但是最大的缺陷就是在某些情况下不适用

举例：纸币问题

比如面额有1元，2元，5元，10元，20元，50元，100元，那么对于110元来说，可以用贪心从最大面额100元开始找。

但是如果改纸币面额，比如1元，2元，5元，20元，55元，100元，那么如果用到贪心算法，会发现并不能找出最优解（贪心：100+5+5=110  动态规划：55+55=110）

动态规划代码如下：

#include <bits/stdc++.h>
using namespace std;
 
int dp[10000];
int n; 
int b[6]={1,5,20,50,55,100};
int temp;
int main()
{
	dp[0]=0;
	dp[1]=1;
	dp[5]=1;
	dp[20]=1;
	dp[50]=1;
	dp[55]=1;
	dp[100]=1;
	for(int i=1;i<=10000;i++)
	{
		temp=10000;
		for(int k=0;k<6;k++)
		{
			if(i>=b[k])
			{
				temp=min(dp[i-b[k]]+1,temp);
			} 
		}
		dp[i]=temp;
	}
	for(int i=1;i<10000;i++)
	{
		cout<<i<<"元用"<<dp[i]<<"张"<<endl;
	}
	return 0;
}

2.9  分治（以后更新）

大部分是二分法

2.10  数字分拆到数组中

(2条消息) 把一个数字分拆存到数组内（C/C++）_菜只因C的博客-CSDN博客https://blog.csdn.net/m0_71934846/article/details/128698111?spm=1001.2014.3001.5501

2.11  数字和字符串的互化

求不了子数字，但能求子字符串

例题：超级质数

(2条消息) 超级质数（蓝桥杯C/C++算法赛）_菜只因C的博客-CSDN博客https://blog.csdn.net/m0_71934846/article/details/128723978?csdn_share_tail=%7B%22type%22%3A%22blog%22%2C%22rType%22%3A%22article%22%2C%22rId%22%3A%22128723978%22%2C%22source%22%3A%22m0_71934846%22%7D

2.12  排序

(4条消息) 找字符串中最大字符（三种快速方法）_求字符串中最大的字符_菜只因C的博客-CSDN博客https://blog.csdn.net/m0_71934846/article/details/128457227?spm=1001.2014.3001.5501

2.13  冒泡排序法和二分查找法（最常用）

冒泡排序法和二分查找法（C/C++）_菜只因C的博客-CSDN博客冒泡排序法和二分查找法（C/C++）https://blog.csdn.net/m0_71934846/article/details/128757285?spm=1001.2014.3001.5502

2.14  图论

图论（入门版）_菜只因C的博客-CSDN博客https://blog.csdn.net/m0_71934846/article/details/128757672?spm=1001.2014.3001.5501

2.15  常用树

蓝桥杯常用树模板（C/C++）_菜只因C的博客-CSDN博客蓝桥杯常用树模板（C/C++）https://blog.csdn.net/m0_71934846/article/details/128764616?csdn_share_tail=%7B%22type%22%3A%22blog%22%2C%22rType%22%3A%22article%22%2C%22rId%22%3A%22128764616%22%2C%22source%22%3A%22m0_71934846%22%7D

2.16  快速幂算法

快速幂算法（C/C++）_菜只因C的博客-CSDN博客https://blog.csdn.net/m0_71934846/article/details/128772642?csdn_share_tail=%7B%22type%22%3A%22blog%22%2C%22rType%22%3A%22article%22%2C%22rId%22%3A%22128772642%22%2C%22source%22%3A%22m0_71934846%22%7D

2.17  素数（质数）

质数（Prime number，又称素数），指在大于1的自然数中，除了1和该数自身外，无法被其他自然数整除的数（也可定义为只有1与该数本身两个正因数的数）

2.17.1  暴力法

两层循环，第一层循环i遍历大于等于2的所有数，第二层循环遍历大于1小于i的所有数j，判断i%j！=0一直成立，则该数为质数

这种方法虽然思路简单，但时间复杂度有时不能满足题目要求

2.17.2  线性筛

定理：一个质数*任何一个不为1的正整数=合数

有了定理之后，就可以通过定理优化代码降低时间复杂度，下面是具体思路

Eratosthenes筛选方法（Eratosthenes Sieve Method）

假设有一个筛子存放1～N，例如：

2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 .........N

先将  2的倍数  筛去：

2 3 5 7 9 11 13 15 17 19 21..........N

再将  3的倍数  筛去：

2 3 5 7 11 13 17 19..........N

 之后，再将5的倍数筛去，再来将7的质数筛去，再来将11的倍数筛去........，如此进行到最后留下的数就都是质数，这就是Eratosthenes筛选方法（Eratosthenes Sieve Method）。

代码：

#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
int primes[1000000];
int cnt;
bool notprime[1000000];

void set_prime()
{
	notprime[1]=true;
	primes[0]=0;
	for(int i=2;i<1000000;i++)
	{
		if(!notprime[i])
		{
			primes[++primes[0]]=i;
		}
		for(ll j=(ll)i*i;j<1000000;j+=i)//保证每一个遍历的值都没被筛过
		{
			notprime[j]=true;
		}
	}
} 

int main()
{
	set_prime();
	for(int i=1;i<=primes[0];i++)
	{
		cout<<primes[i]<<endl;
	}
	return 0;
}

2.18  递归

是指函数/过程/子程序在运行过程序中直接或间接调用自身而产生的重入现象。

在计算机编程里，递归指的是一个过程：函数不断引用自身，直到引用的对象已知。

使用递归解决问题，思路清晰，代码少。但是在主流高级语言中（如C语言、Pascal语言等）使用递归算法要耗用更多的栈空间，所以在堆栈尺寸受限制时（如嵌入式系统或者内核态编程），应避免采用。所有的递归算法都可以改写成与之等价的非递归算法。

递归的重点是找到递归表达式

例1：阶乘

#include <bits/stdc++.h>
using namespace std;
int f(int n)
{
	if(n==1)
	{
		return 1;
	}
	return n*f(n-1);
}
int main()
{
	cout<<f(10);
	return 0;
}

例2：汉诺塔 

汉诺塔+汉诺四塔（C/C++）_菜只因C的博客-CSDN博客汉诺塔（C/C++）https://blog.csdn.net/m0_71934846/article/details/128796546?csdn_share_tail=%7B%22type%22%3A%22blog%22%2C%22rType%22%3A%22article%22%2C%22rId%22%3A%22128796546%22%2C%22source%22%3A%22m0_71934846%22%7D

2.19  STL

(2条消息) STL使用方法（C++）_菜只因C的博客-CSDN博客icon-default.png?t=N0U7https://blog.csdn.net/m0_71934846/article/details/128843820?csdn_share_tail=%7B%22type%22%3A%22blog%22%2C%22rType%22%3A%22article%22%2C%22rId%22%3A%22128843820%22%2C%22source%22%3A%22m0_71934846%22%7D

这里大概列出参加蓝桥杯需要掌握的知识点和技巧，若想详细了解某个知识点，可以看看我的例题和别人的博文。

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/192408.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

Shield UI for JavaScript 1.7.44 Crack

Shield UI for JavaScript 1.7.44 Crack

Shield UI for JavaScript Shield UI JavaScript 框架提供具有响应式设计的 JavaScript HTML5 组件&#xff0c;这些组件经过优化以获得最佳性能。 Shield UI 在 70 多种小部件类型中提供了最快和高度可定制的网格和图表控件。每个单独的控件都由行业领先的 24/7 支持包提供支持…
阅读更多...
以莫罗湾为例，利用高精度地形高程模型应对海岸环境变化

以莫罗湾为例，利用高精度地形高程模型应对海岸环境变化

Morro Bay是位于加州 San Luis Obispo附近的浅海河口区&#xff0c;存在大量野生动物&#xff0c;也是人们户外活动的好去处。但是沉积变化和鳗草&#xff08;大叶藻&#xff09;的大量消失对河口景观产生了不利影响。为了更好地认识环境改变的路径并提取修复对策&#xff0c;M…
阅读更多...
2023年山东最新建筑八大员（资料员）考试试题题库及答案

2023年山东最新建筑八大员（资料员）考试试题题库及答案

百分百题库提供建筑八大员&#xff08;资料员&#xff09;考试试题、建筑八大员&#xff08;资料员&#xff09;考试预测题、建筑八大员&#xff08;资料员&#xff09;考试真题、建筑八大员&#xff08;资料员&#xff09;证考试题库等,提供在线做题刷题&#xff0c;在线模拟考…
阅读更多...
Vue实战第3章：主页设计之顶部导航栏

Vue实战第3章：主页设计之顶部导航栏

主页设计之顶部导航栏 前言 本篇在讲什么 本篇文章主要来制作一个导航栏&#xff0c;具体效果就按照下图来处理吧 本篇适合什么 适合初学Vue的小白 想了解建站的同学 本篇需要什么 对Html语法有简单认知 对CSS语法有简单认知 对Vue有简单认知 依赖VS Code编辑器 本…
阅读更多...
【redis6】第十三章（主从复制）

【redis6】第十三章（主从复制）

是什么 主机数据更新后根据配置和策略&#xff0c; 自动同步到备机的master/slaver机制&#xff0c;Master以写为主&#xff0c;Slave以读为主 能干嘛 读写分离&#xff0c;性能扩展 容灾快速恢复 怎么玩 拷贝多个redis.conf文件include(写绝对路径) 开启daemonize yes Pi…
阅读更多...
连接mysql5.7错误1045，重新设置root用户密码，已经springboot连接配置

连接mysql5.7错误1045，重新设置root用户密码，已经springboot连接配置

错误&#xff1a; ERROR 1045 (28000): Access denied for user ‘root’‘localhost’ (using password: NO) 原因是&#xff1a; 是因为数据库中用户密码的问题。所以我们可以跳过数据权限验证&#xff0c;重新设置一下 一、修改my.ini配置文件 停止mysql服务 方法&#xff…
阅读更多...
GJB 5000B二级-PMC项目监控

GJB 5000B二级-PMC项目监控

一、主要变化情况 新增2项（红色）、拆分3项（蓝色）、移除2项（黄色）、合并9项（绿色） 新增的主要内容-2项 增加多资源计划的监控要求：   军用软件系统具体设备间联系紧密，测试验证环节多、要求高等特点，其研发和测试需要众多软硬件资源支持，而这些资源往往是影响…
阅读更多...
ConcurrentHashMap1.7和1.8的不同实现

ConcurrentHashMap1.7和1.8的不同实现

ConcurrentHashMap 在多线程环境下&#xff0c;使用HashMap进行put操作时存在丢失数据的情况&#xff0c;为了避免这种bug的隐患&#xff0c;强烈建议使用ConcurrentHashMap代替HashMap&#xff0c;为了对更深入的了解&#xff0c;本文将对JDK1.7和1.8的不同实现进行分析。 J…
阅读更多...
FreeRTOS中断管理 | FreeRTOS五

FreeRTOS中断管理 | FreeRTOS五

目录 说明&#xff1a; 一、中断基础 1.1、中断理解 1.2、中断执行步骤 1.3、中断寄存器选择位 1.4、中断优先级分类 二、中断优先级分组设置 2.1、分类 2.2、特点 三、中断有关寄存器 3.1、SHPR1寄存器 3.2、SHPR2寄存器 3.3、SHPR3寄存器 3.4、FreeRTOS中配置Pe…
阅读更多...
最优传输问题与Sinkhorn算法

最优传输问题与Sinkhorn算法

目录引言例子&#xff1a;分甜点最优传输问题Sinkhorn算法Sinkhorn距离算法流程代码实验引言 最近看到一篇特征匹配相关的论文&#xff0c;思想是将特征匹配问题转化为最优传输问题求解&#xff0c;于是我去学习了一下最优传输问题。 本文主要是对博文 Notes on Optimal Trans…
阅读更多...
4.6 QR分解二：Householder变换

4.6 QR分解二：Householder变换

1 Householder reflector Householder反射是这样子的(图片来自瑞典皇家理工学院)&#xff1a;   图中u是长度为1的向量。x是任意向量&#xff0c;H是u的Householder reflector。可见无论x是什么向量&#xff0c;HxHxHx始终除于和u正交的平面上。H和u的关系是&#xff1a; HI…
阅读更多...
【z-library平替】Clibrary中文图书馆，电子书大全

【z-library平替】Clibrary中文图书馆，电子书大全

目录1、z-library和Clibrary简介2、Clibrary网址3、具体操作界面1、z-library和Clibrary简介 喜欢阅读的盆友多多少少可能都听过z-library&#xff0c;书籍库非常全&#xff0c;而且是免费的&#xff0c;但是在z-library国内下线后&#xff0c;就一直没有找到合适的平替书库。 …
阅读更多...
【vue2】vuex超超超级详解！(核心五大配置项)

【vue2】vuex超超超级详解！(核心五大配置项)

&#x1f973;博 主&#xff1a;初映CY的前说(前端领域) &#x1f31e;个人信条&#xff1a;想要变成得到&#xff0c;中间还有做到&#xff01; &#x1f918;本文核心&#xff1a;vuex基础认识、state、getters、mutations actions、modules使用 目录(文末原素材) 一、…
阅读更多...
新年找工作？python带你批量采集招聘数据

新年找工作？python带你批量采集招聘数据

前言 大家早好、午好、晚好吖 ❤ ~ 必备素材: stealth.min.js 谷歌浏览器谷歌驱动selenium3.141.0 不知道怎么弄嘚同学可以私我获取哦~ 开发环境: python 3.8 pycharm 专业版 操作步骤 selenium 模块: 操作浏览器 打开一个浏览器 打开一个网址 获取数据 保存数据 …
阅读更多...
性能测试工具-nmon

性能测试工具-nmon

nmon 文章目录nmon介绍下载Linux系统服务器在服务器上新建nmon文件夹将下载文件上传到服务器新建的文件夹内修改文件名启动nmon启动nmon命令行使用nomn_analyser对监控结果进行分析图表分析nmon 主要用来做性能测试时对服务器的监控 捕捉各类系统资源的使用情况&#xff0c;并…
阅读更多...
Maven实战-2.pom.xml标签说明

Maven实战-2.pom.xml标签说明

前言 持续更新中… pom.xml文件 1.<project> 这是pom.xml的根元素&#xff0c;所有的标签都包含在<project>…</project>之间。 2.<modelVersion> 指定当前POM模型的版本&#xff0c;对于maven2和maven3来说&#xff0c;它只能是4.0.0 <mode…
阅读更多...
【linux】剖析底层——带你详细了解Linux内核源码的构成及其作用（1）

【linux】剖析底层——带你详细了解Linux内核源码的构成及其作用（1）

目录 一、arch文件 1.作用 2.arch文件下的子文件示意图 3.各个子文件的作用 &#xff08;1&#xff09;alpha &#xff08;2&#xff09;arc &#xff08;3&#xff09;arm &#xff08;4&#xff09;arm64 &#xff08;5&#xff09;cshy &#xff08;6&#xff09;…
阅读更多...
8 加载数据集

8 加载数据集

文章目录前提知识了解数据集Mini-Batch常用术语DataLoader核心参数核心功能小tips课程代码实例课程来源&#xff1a; 链接课程文本部分来源&#xff08;参考&#xff09;&#xff1a; 链接以及&#xff08;强烈推荐&#xff09; Birandaの前提知识了解 enumerate函数 数据集 …
阅读更多...
局域网中UTP连接，如何实现防止芯片损坏，防止信号产生各种误码，及实现CHIP之间的阻抗匹配

局域网中UTP连接，如何实现防止芯片损坏，防止信号产生各种误码，及实现CHIP之间的阻抗匹配

Hqst盈盛电子导读&#xff1a;局域网中UTP连接&#xff0c;如何实现防止芯片损坏&#xff0c;防止信号产生各种误码&#xff0c;及实现CHIP之间的阻抗匹配&#xff0c;浅谈网络滤波器作用一&#xff0c;在有线局域网中&#xff0c;计算机与服务器之间&#xff0c;计算机与路由器…
阅读更多...
10、条件语句

10、条件语句

目录 一、if语句的基本形式 1. if语句形式 2. if…else语句形式 3. else if语句形式 二、if的嵌套形式 三、条件运算符 四、switch语句 1. switch语句的基本形式 2. 多路开关模式的switch语句 一、if语句的基本形式 在if语句中&#xff0c;首先判断表达式的值&#x…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023