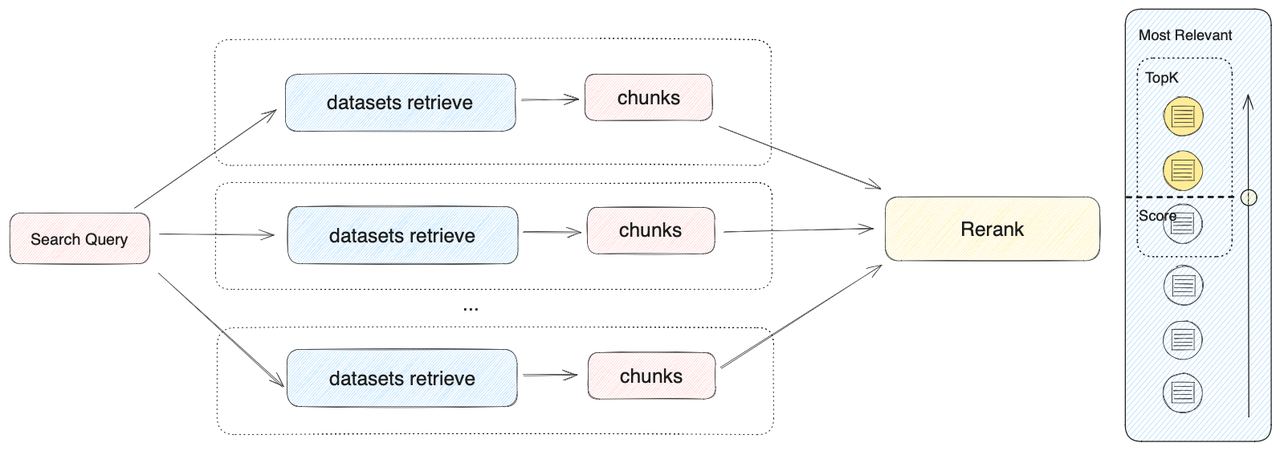
对于这个题，如何处理同一个方向的问题，且对于同一组的如果间隔太大如何实现离散化

#include<bits/stdc++.h>
using namespace std;

#define int long long
typedef long long ll;
map<pair<int,int>,vector<pair<ll,ll>>> mp;  // 注意里面是用vector装着 
signed main(){
	int n;
	cin >> n;
	int ans = 0;
	int num = 0;
	for(int i=1;i<=n;i++){
		int a,b,c;
		cin >> a >> b >> c;
		int d= abs(__gcd(a,b));  // 请注意这个 gcd 是两个下划线
		// 且要取绝对值 
		mp[{a/d,b/d}].push_back({a*a+b*b,c});
		ans += c;
	}
	for(auto u:mp){
		vector<pair<ll,ll>> t = u.second;
		sort(t.begin(),t.end());
		int len = t.size();
		for(int i=0;i<len;i++){
			if(t[i].second!=1) num++;
			else if((i+1)==len || t[i+1].second!=1) num++;
		}
	}
	cout << ans << " " << num;
	return 0;
}

#include<bits/stdc++.h>
using namespace std;

const int N = (int)1e3 + 5;
int e[N * N], ne[N * N], h[N], idx = 0;
int energy[N * N], va[N * N];
int vis[N];
int di[N];

void add(int a, int b, int ener, int value) {
    e[++idx] = b;
    ne[idx] = h[a]; h[a] = idx;
    energy[idx] = ener, va[idx] = value;
}
int n, m;
int maxdistance = 0xfffffff;
int start;  // 设置为全局变量

int dikj() {
    priority_queue<pair<int, int>> q;
    int ma = 0;
    //vis[start] = 1; // 记录一下
    for (int i = 0; i <= n; i++) vis[i] = 0,di[i] = 0xffffff;
    //vis[start] = 1;
    q.push({ 0,start });
    while (q.size()) {
        int dis = -q.top().first, node = q.top().second;
        q.pop();
        if (vis[node]) continue;
        vis[node] = 1;
        for (int i = h[node]; i != -1; i = ne[i]) {
            int to = e[i];
            //if (vis[to]) continue;
            //vis[to] = 1;
            int newdis = energy[i] + dis; // 这是新的距离
            if (newdis < di[to]) {
                di[to] = newdis;
                q.push({ -newdis, to });
            }
           /* ma = max(ma, newdis);*/
            
        }
    }
    for (int i = 1; i <= n; i++) {
        if (di[i] == 0xffffff) continue;
        ma = max(ma, di[i]);
    }
    return ma;
}
int pre[N];// 记录前缀
int ju[N];
void solve(int start) {
    for (int i = 1; i <= n; i++) {
        pre[i] = i, vis[i] = 0, di[i] = 0xffffff;
    }
    priority_queue<pair<int, int>> q;
    q.push({ 0,start });
    //vis[start] = 1;
    while (q.size()) {
        int dis = -q.top().first, node = q.top().second;
        q.pop();
        //
        if (vis[node]) continue;
        vis[node] = 1;
        for (int i = h[node]; i != -1; i = ne[i]) {
            int to = e[i];
            //if (vis[to]) continue;
            //vis[to] = 1;
            int t = dis + energy[i];
            if (t < di[to]) {
                di[to] = t; pre[to] = node;
                ju[to] = ju[node] + va[i];
                q.push({ -t,to });
                //cout << "1 to: " << to << " node " << node << endl;
            }
            else if (t == di[to]) {
                int u = ju[node] + va[i];
                if (u > ju[to]) {
                    di[to] = t; pre[to] = node;
                    ju[to] = ju[node] + va[i];
                    //q.push({ -t,to });
                    //cout << "2 to: " << to << " node " << node << endl;
                }
            }
        }
    }
}


void print(int s, int t) {
    if (s == t) {
        printf("%d", s);
        return;
    }
    print(s, pre[t]);
    printf("->%d", t);

}
int main() {
    cin >> n >> m;
    memset(h, -1, sizeof h);
    for (int i = 1; i <= m; i++) {
        int a, b, c, d;
        cin >> a >> b >> c >> d;
        add(a, b, c, d);
        add(b, a, c, d);
    }
    int kaishi;
    for (int i = 1; i <= n; i++) {
        start = i;
        int d = dikj();
        //cout << d << endl;
        if (d < maxdistance) {
            kaishi = start;
            maxdistance = d;
        }
    }

    cout << kaishi << endl;
    solve(kaishi);
    //int o = kaishi;
    int t;
    cin >> t;
    //for (int i = 1; i <= n; i++) {
    //    cout << pre[i] << endl;
    //}
    di[kaishi] = ju[kaishi] =0 ;
    for (int i = 1; i <= t; i++) {
        int a;
        cin >> a;
        print(kaishi,a);
        cout << endl;
        cout << di[a] << " " << ju[a] << endl;
    }
}