1.引言
在完成环境配置之后,我们需要开始实际的编译工作。编译 Chromium 是一个相对复杂且耗时的过程,尤其是第一次编译时。为了保证顺利完成,我们将使用 GN 和 Ninja 工具来生成和管理构建文件。接下来,我们会详细介绍如何生成构建文件并进行编译。
2.编译Chromium
完成runhooks后就可以使用gn生成构建文件了,Chromium 使用 Ninja 作为主要的编译工具,并使用名为 GN 的工具生成 .ninja 文件。你可以创建任意多个不同配置的编译目录。要创建编译目录,请运行
gn gen out/Default这里Default可以是别的名字,但是一定要是out的子目录,这里我们使用Default作为目录名

接下来,使用 Ninja 命令构建 Chromium("chrome "目标):
autoninja -C out/Default chrome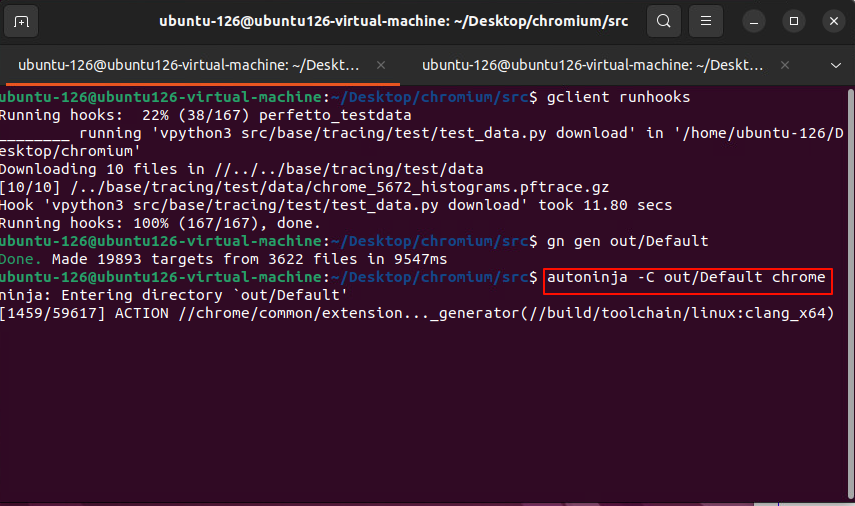
最后耐心等待,依据电脑性能会编译不同的时间,一般在五六小时左右,如果中途编译中断了也没关系,重新输入命令,之前编译完毕的不会消失,ninja会自动继续编译

这样就编译好了,前面显示583/583的原因是我中断了一次编译后继续编译的,我们打开编译完成的Chromium看一下
./out/Default/chrome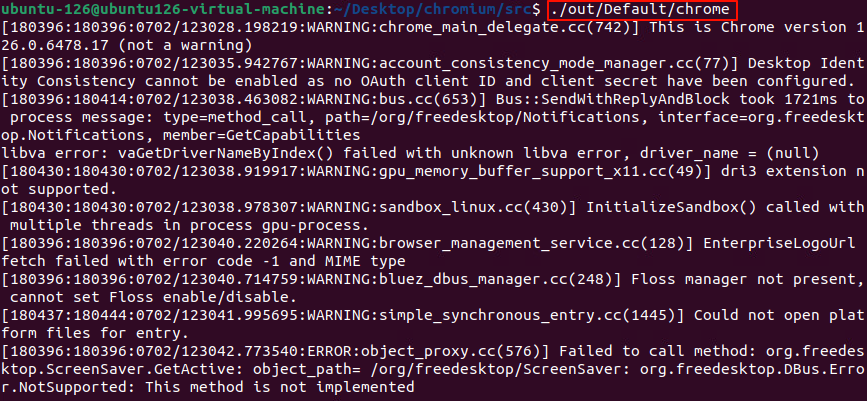
可以看到有一些报错,但是Chrome成功开启了

3.结尾
至此,我们已经成功地完成了Chromium的编译,并且可以启动并运行它。然而,在首次编译后,你可能会遇到一些启动时的警告和错误信息。接下来,我们将详细分析这些报错信息,并提供相应的解决方案或建议,以确保你的编译环境和运行环境的稳定性。