分治—归并
- 1.排序数组
- 2.交易逆序对的总数
- 3.计算右侧小于当前元素的个数
- 4.翻转对

点赞👍👍收藏🌟🌟关注💖💖
你的支持是对我最大的鼓励,我们一起努力吧!😃😃
1.排序数组
题目链接:912. 排序数组
题目描述:

算法原理:
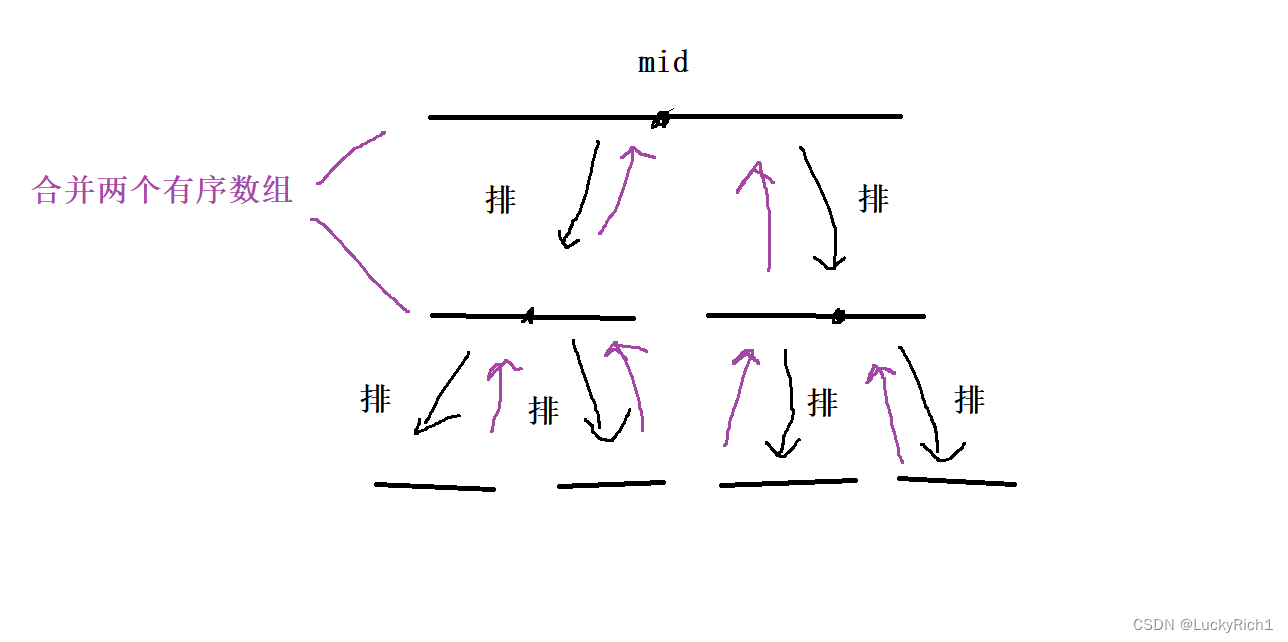
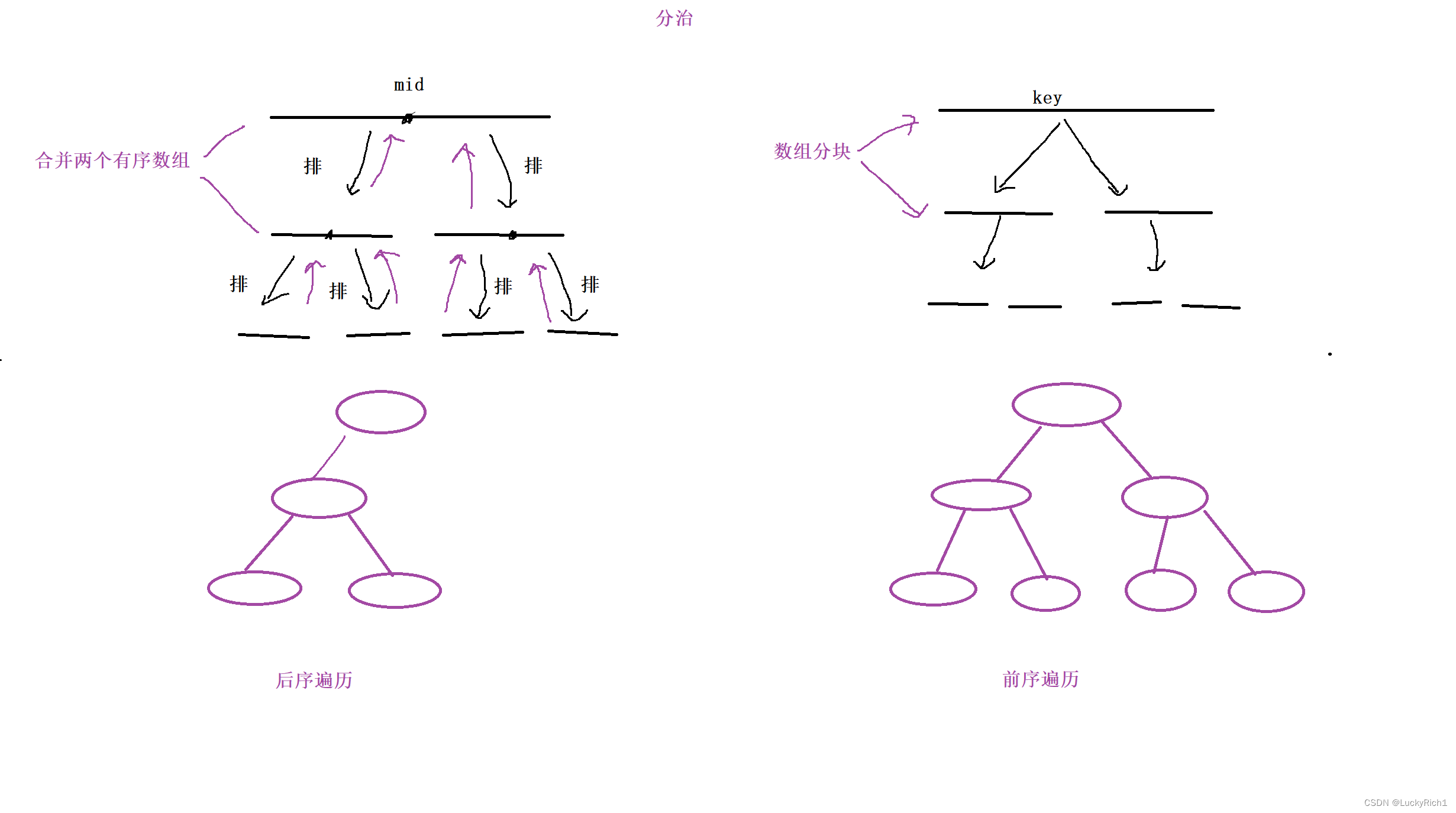
归并排序的核心思想就是,选一个中间节点,将数组分成左右两区间,先将左边排排序相当于又是一个归并过程,选一个中间节点然后在把左边排序,当区间只有一个元素就可以向上返回。左边拍完序,在对右边排排序,当左右排好序后在合并,选择小的插入,然后拷贝回原数组。
快速排序就是选择一个key将数组分块,然后左右继续指向数组分块的核心操作,当数组被分成一个元素或者没有元素就结束分块。
所以说快排和归并非常类似,无非就是处理数组时间不一样。归并画成树就是一个后序,先处理左在处理右然后将左右合并,快排就是一个前序,先把数组分两块,然去搞左边,左边还是找一个key然后分成左和右。。。
class Solution {
public:
vector<int> tmp;
vector<int> sortArray(vector<int>& nums) {
int n = nums.size();
tmp.resize(n);
Mergesort(nums, 0, n-1);
return nums;
}
void Mergesort(vector<int>& nums, int left, int right)
{
if(left >= right) return;
// 1. 选择中间点划分区间
int mid = left + (right - left) / 2;
//[left ,mid] [mid+1, right]
// 2.把左右区间排序
Mergesort(nums, left, mid);
Mergesort(nums, mid + 1, right);
// 3.合并两个有序数组
int cur1= left, cur2 = mid + 1, i = 0;
while(cur1 <= mid && cur2<= right)
tmp[i++] = nums[cur1] < nums[cur2] ? nums[cur1++] : nums[cur2++];
while(cu1 <= mid) tmp[i++] = nums[cur1++];
while(cur2<= right) tmp[i++] = nums[cur2++];
// 4.拷贝回原数组
for(int i = left; i <= right; ++i)
nums[i] = tmp[i - left];
}
};
2.交易逆序对的总数
题目链接:LCR 170. 交易逆序对的总数
题目分析:

逆序对是两个数前面的数比后面的大就是逆序对。
算法原理:
解法一:暴力解法->暴力枚举
把所有二元组枚举出来看看是不是逆序对。两层for循环,但是超时。
如果想求整个数组的逆序对的时候,我把数组按照中间点分成两部分,然后求整个数组逆序对的时候,先求出左边逆序对的个数假设是a,在求出右边逆序对的个数假设是b,然后左边挑一个数右边挑一个数求出一左一右的逆序对个数假设是c。那a+b+c 就是整个逆序对个数。因为本质还是暴力枚举。
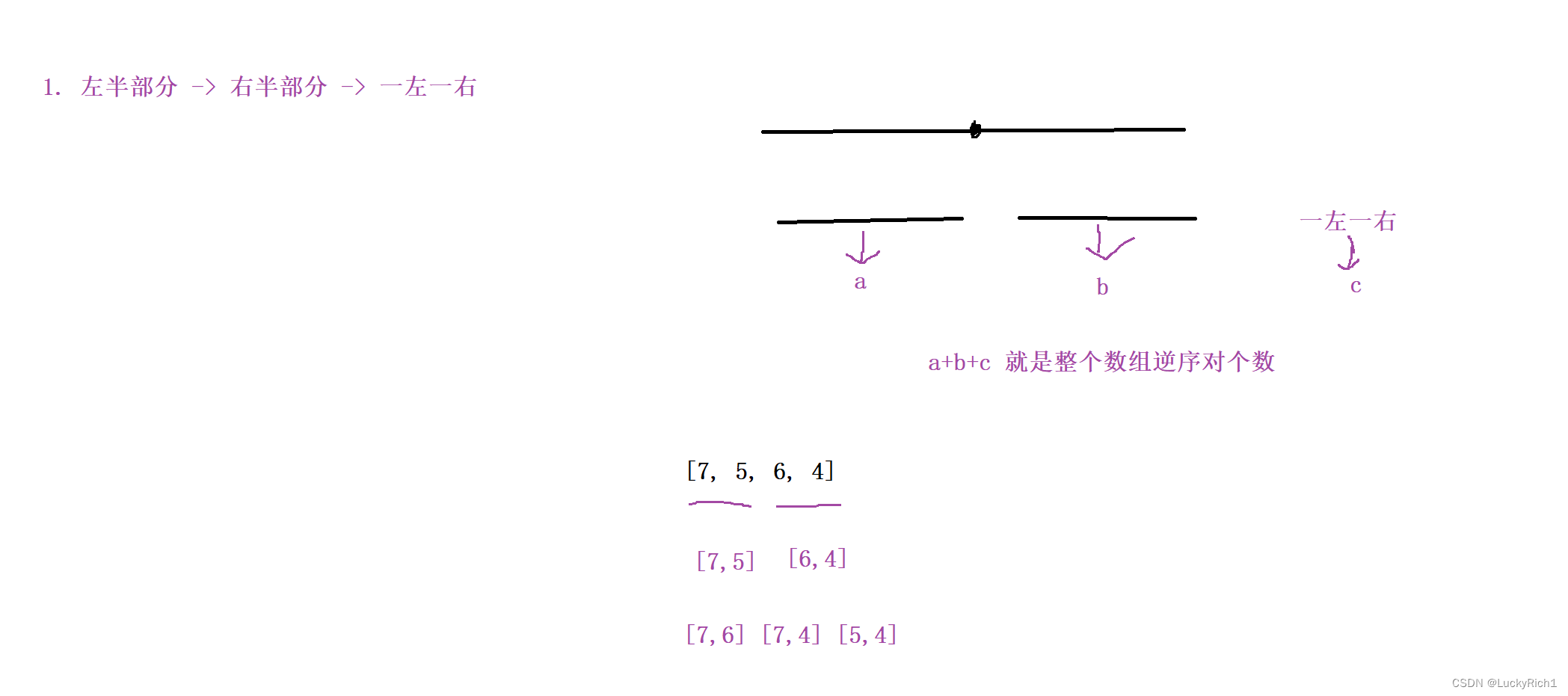
接下来我们在扩展一下,左半部分挑完之后排个序,右半部分跳完之后也排个序,然后左右都有序了在一左一右挑。这也是正确的,因为左半部分挑出来a后在排序不会影响结果, 右半部分挑出来b后在排序也不会影响结果。无非影响的是一左一右。但是我们左边挑一个右边挑一个是不管顺序的。我们从左边挑选一个数,然后在从右边挑选比我小的数的个数就行了,从右边挑选一个数,然后在从左边挑选比我大的数的个数就行了,至于有没有序和我没关系。

当到这里的时候你会发现其实就是一个归并排序。
解法二:利用归并排序解决问题
选择中间点把数组分成两份,先去左区间找,如果左区间太大还可以在选个中间点在把数组分开直到不能分了就找逆序对,同理右边也是。最后一左一右去找逆序对,这个策略正好对应归并的过程。左半部分和右边部分可以在递归中完成,我们的核心就是解决一左一右。同样左边部分+左排序放在一起递归中完整,右半部分+右排序放在一起递归完成,我们核心还是处理一左一右。因为递归都是的统一,所以一左一右后面在加一个排序。
左半部分 + 左排序 + 右半部分 + 右排序 + 一左一右 + 排序
这个时候有个小问题为什么非要排序呢?
虽然会有空间的开销,但是会变得非常快。
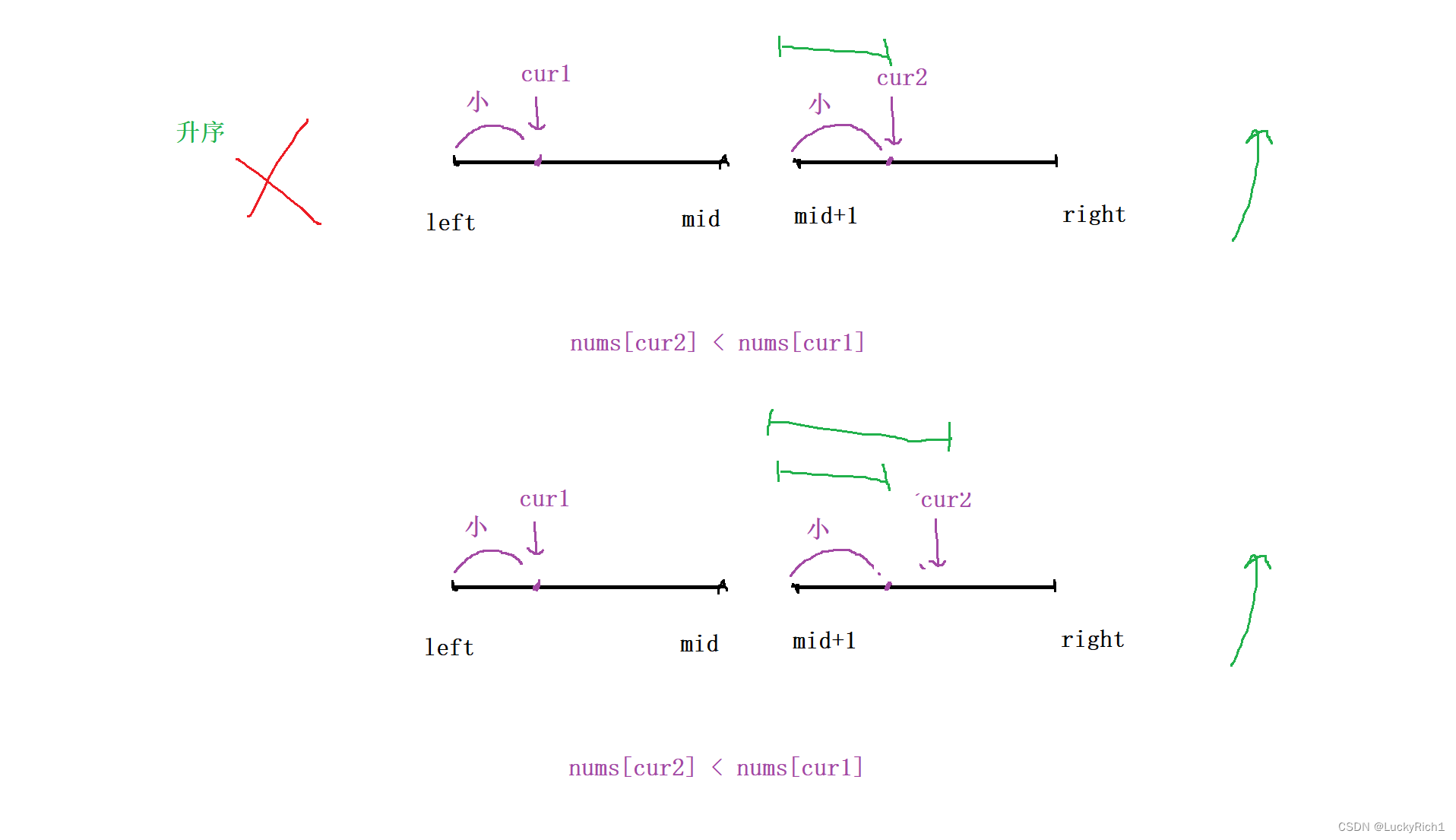
利用归并排序后,数组左右区间已经是有序的了。假设是升序的。cur1和cur2之前的都是都是比cur1和cur2小的元素。
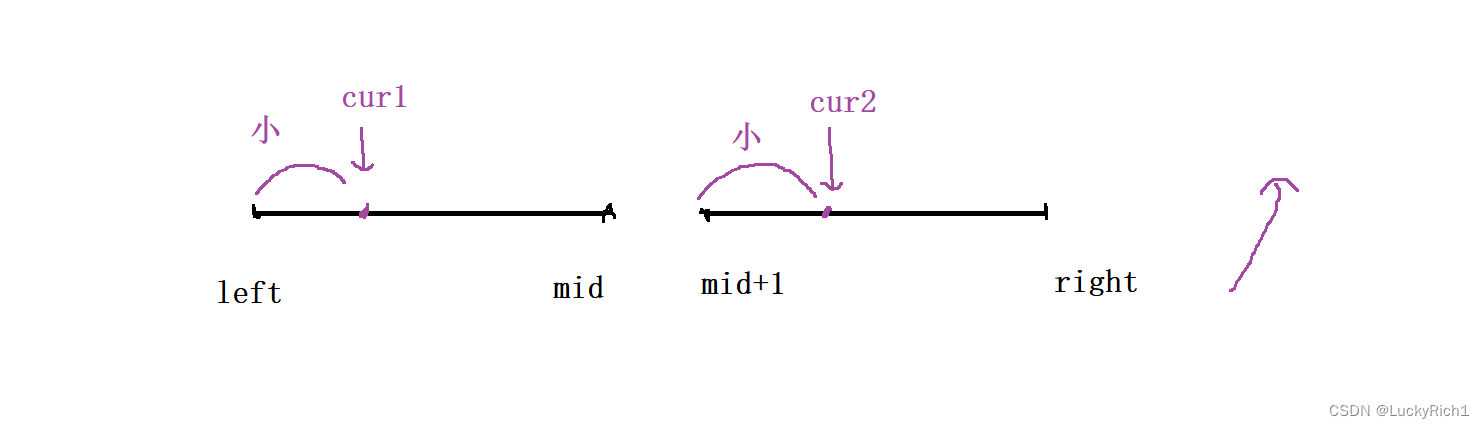
此时统计逆序对的话,按照如下策略可以一次找到一堆逆序对。
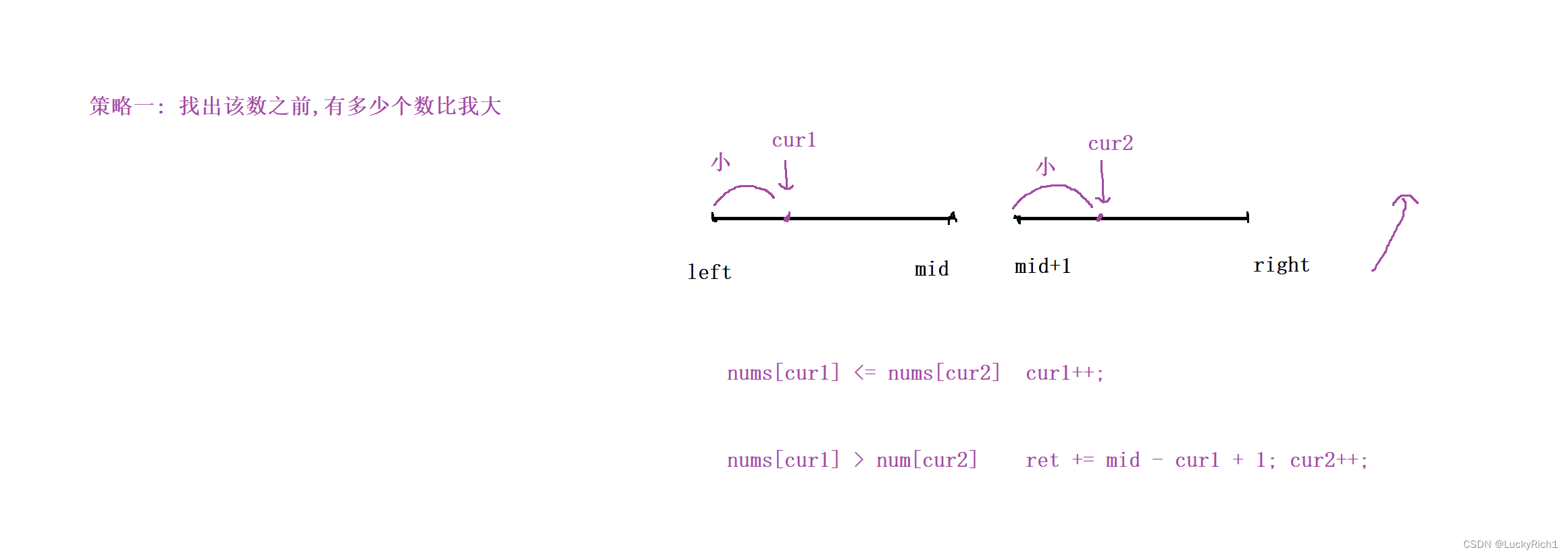
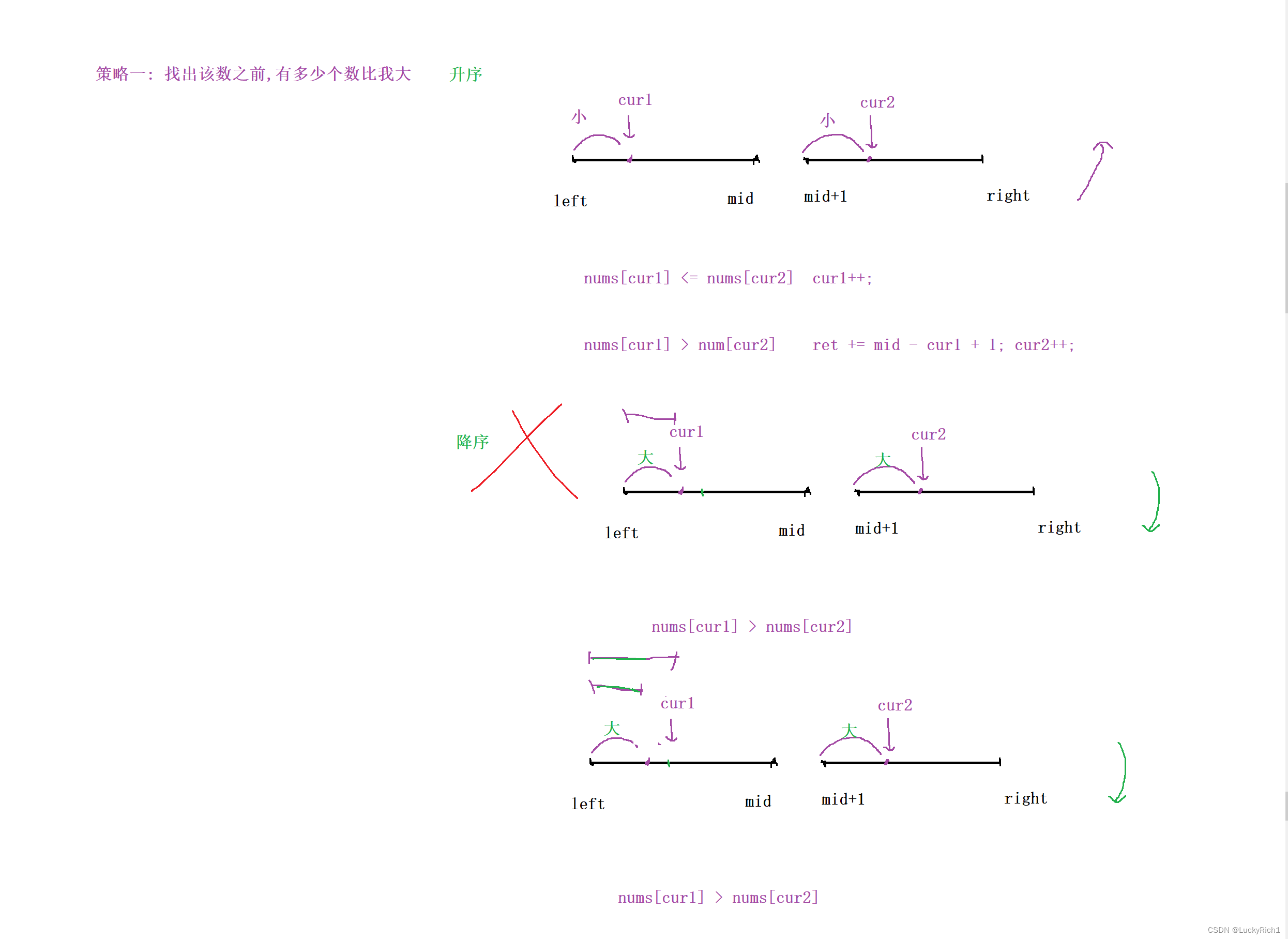
策略一:找出该数之前,多少个数比我大
此时我们固定的是cur2,因为我们是一左一右找,想要找比我大的数,盯的是后面的数,去看看左半部分有多少个比我大。此时就和归并排序完美契合。无非就是三种情况。
当 nums[cur1] < nums[cur2],说明还没有在左边找到比cur2大,所以cur1++
当 nums[cur1] == nums[cur2],还是没有在左边找到比cur2大,所以cur1++
上面两种情况可以合在一起
nums[cur1] <= nums[cur2], cur1++,注意别忘记放进归并数组里。
当 nums[cur1] > num[cur2] ,当前cur1比cur2元素大,别忘记我们可是升序数组,而且cur1比cur2的时候是cur1第一次出现比cur2大,cur1后面的元素都是比cur2大的!此时我们就是根据归并排序的一次比较就找到一堆cur1比cur2大的数。此时用一个变量记录一下cur1位置到左边结束的位置的个数就可以了。ret += mid - cur1 + 1,一次就统计出来一大堆。而且cur1比cur2大的时候,我们下一次想让cur2向后移,这正好和归并排序一样,让小的往后移。
时间复杂度O(nlogn)
当前策略 找出该数之前,多少个数比我大,对于数组升序是没问题的,那这个数组是降序的能不能解决这个问题,只要找比我大的不管升序还是降序都是固定cur2,在左边找比cur2大的。
此时如果nums[cur1] > nums[cur2] ,要统计左边开始到cur1有多个元素,但是有一个致命问题,cur1往前走一步的位置可能继续比cur2大,还是要统计左边开始到cur1有多个元素。然后你就会发现重复了。
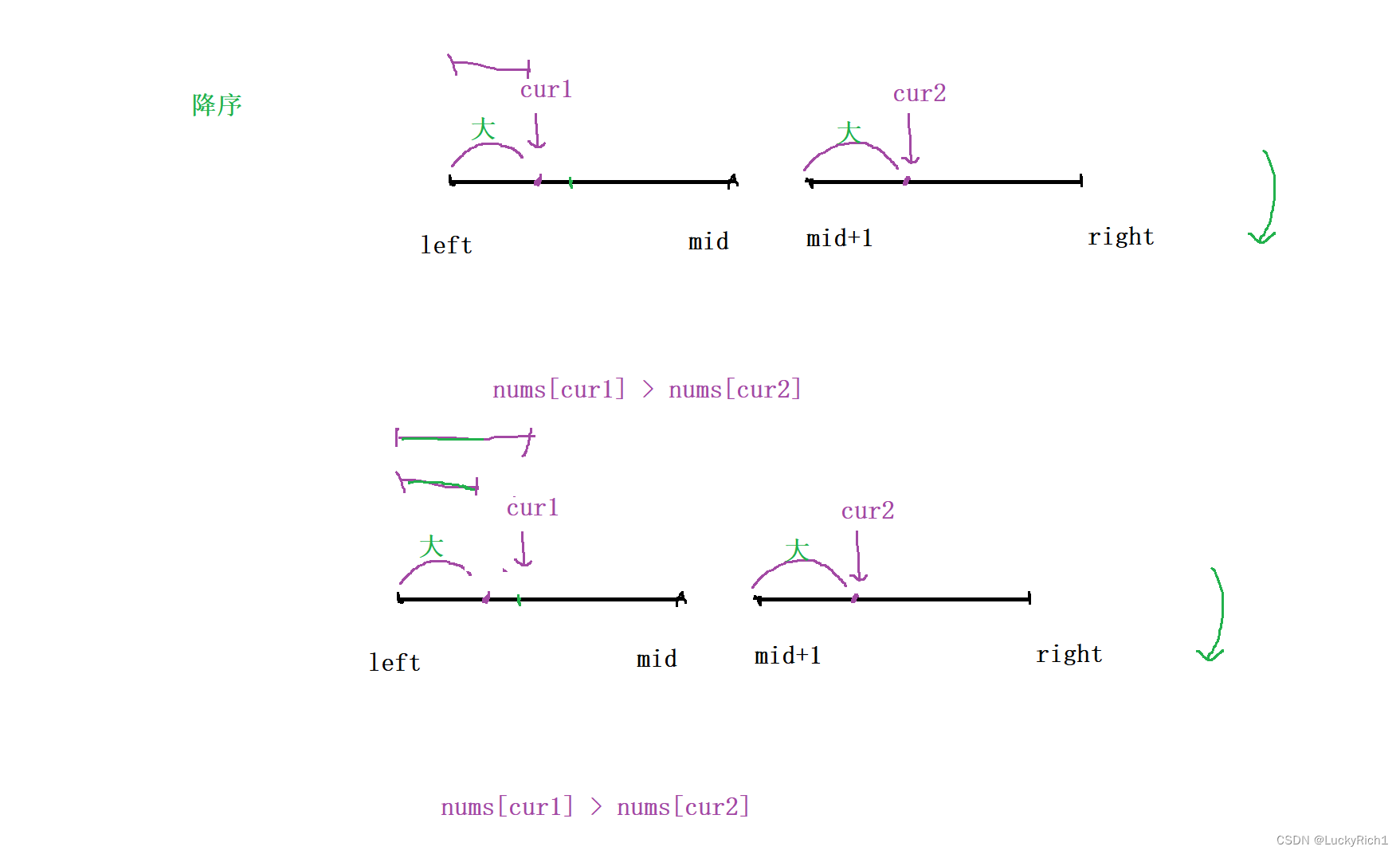
因此 策略一 :找出该数之前,多少个数比我大 只能是升序,不能是降序!
固定cur2
那降序就没有用武之地了嘛?并不是。
策略二 :找出该数之后,有多少个数比我小 只能是降序
固定cur1,在右边部分找比cur1小的。当cur1比cur2大的时候,cur2是第一个出现的因为又是降序所以cur1比cur2后面元素都大,此时直接统计个cur2到右区间的个数 ret += right - cur2 + 1。而且统计完个数之后,已经把比cur1小的都找到了,此时让cur1右移,而且正好和归并排序是一样的。
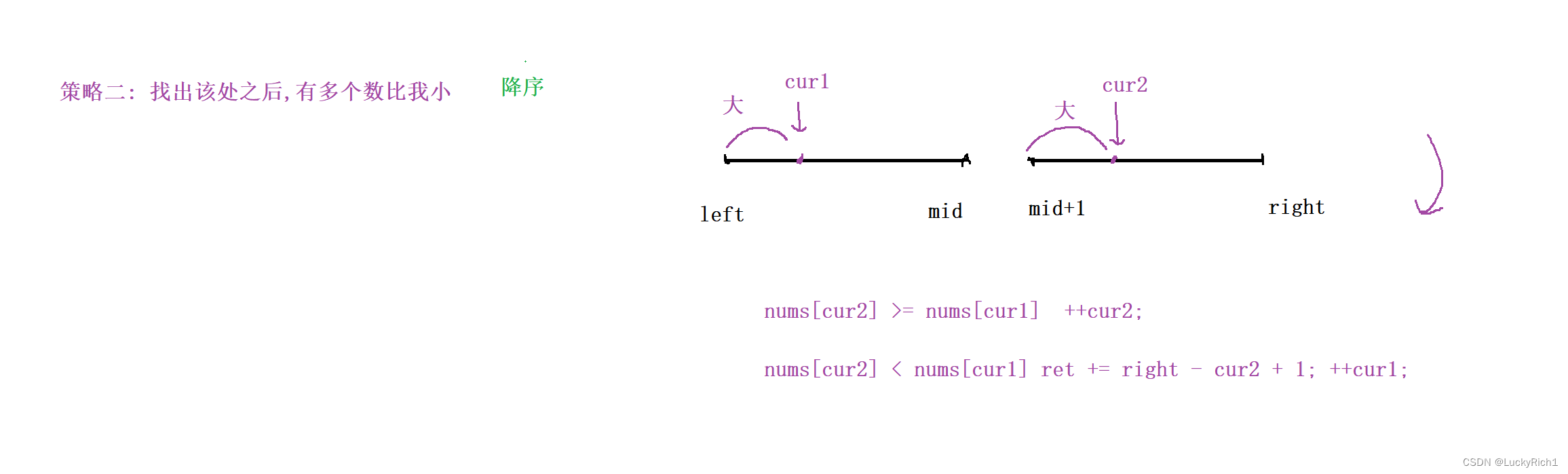
如果是升序的话也会有重复计算的问题。
至此算法原理就结束了,其实就是利用前两部分析出来这道题可以用分治的方法来做。想求整个数组的逆序数,我可以先求左区间逆序数,在求右区间逆序数,然后一左一右挑一个求逆序数。所以这就是一个分支。然后发现数组有序的话可以通过一次比较统计一大推,因此可以用归并排序来解决这个问题。
class Solution {
vector<int> tmp;
public:
int reversePairs(vector<int>& record) {
int n = record.size();
tmp.resize(n);
return Mergesort(record, 0, n - 1);
}
int Mergesort(vector<int>& nums, int left, int right)
{
if(left >= right) return 0;
int ret = 0;
// 1.找中间节点,将数组分成两部分
int mid = (left + right) >> 1;
//[left,mid] [mid+1,right]
// 2. 左边的个数 + 排序 + 右边的个数 + 排序
ret += Mergesort(nums, left, mid);
ret += Mergesort(nums, mid + 1, right);
// 3. 一左一右的个数
int cur1 = left, cur2 = mid + 1, i = 0;
// while(cur1 <= mid && cur2 <= right) //升序
// {
// if(nums[cur1] <= nums[cur2])
// {
// tmp[i++] = nums[cur1++];
// }
// else
// {
// ret += mid - cur1 + 1;
// tmp[i++] = nums[cur2++];
// }
// }
while(cur1 <= mid && cur2 <= right) //降序
{
if(nums[cur1] <= nums[cur2])
{
tmp[i++] = nums[cur2++];
}
else
{
ret += right - cur2 + 1;
tmp[i++] = nums[cur1++];
}
}
// 4. 处理一下排序
while(cur1 <= mid) tmp[i++] = nums[cur1++];
while(cur2 <= right) tmp[i++] = nums[cur2++];
for(int j = left; j <= right; ++j)
nums[j] = tmp[j - left];
return ret;
}
};
3.计算右侧小于当前元素的个数
题目链接:315. 计算右侧小于当前元素的个数
题目分析:

给一个nums数组,返回一个count数组,count[i] 的值是 对应nums[i] 右侧小于 nums[i] 的元素的数量。
这也是求逆序对,但并不是求总体的逆序对个数,而是每个数的逆序对个数。
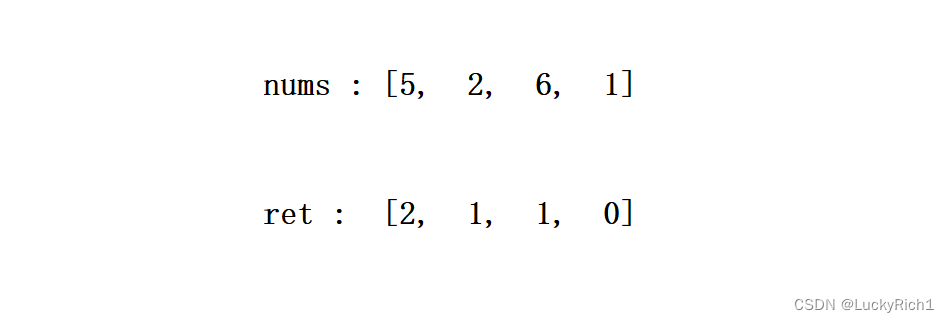
就是给一个数看看右边比我少的有多少个。我们也是可以按照归并排序来处理这个问题,但难得就是这返回数组怎么搞。
算法原理:
解法:归并排序
选择一个中间点,将数组分成左右两部分,先在左半部分找,在到右半部分找,然后一左一右找。
左半部分 + 排序 + 右半部分 + 排序 + 一左一右 + 排序
策略二: 找出该数之后,有多少个数比我小 只能是降序
固定cur1
当 nums[cur1] <= nums[cur2] ,因为是降序此时并没有找到有多少个元素比cur1小,所以不更新结果让cur2++
当 nums[cur1] > nums[cur2] ,第一次出现cur1比cur2,因为是降序所以此时cur2后面所有元素都比cur1小,此时可以统计一大堆,但是我们这里可不是搞一个ret来记录,而是搞一个数组,要把nums[cur1] 对应的 index(下标) 里面的 ret += right - cur2 +1
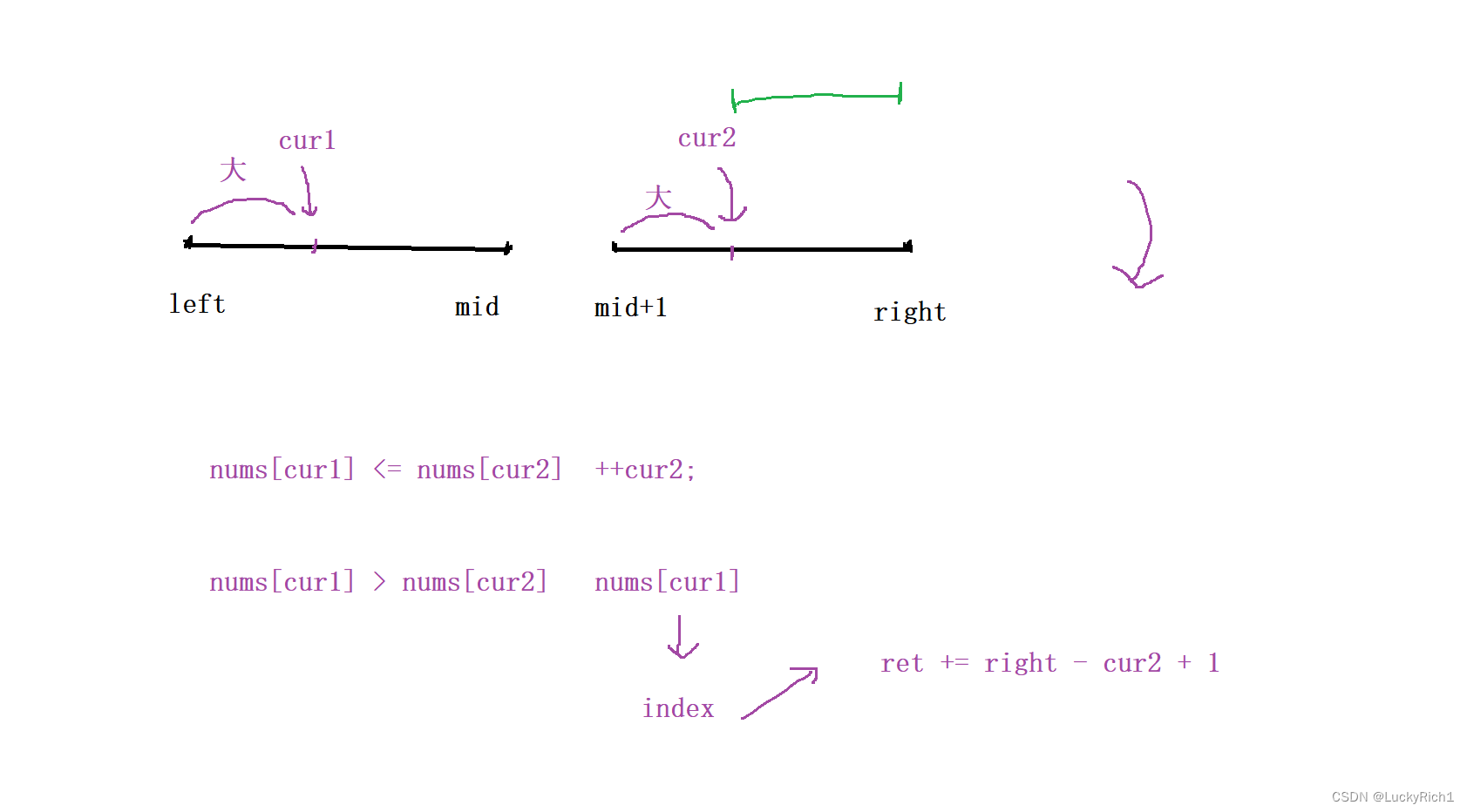
就比如这个数组,当计算出比当前位置元素小的个数是要把结果记录到这个元素对应的位置上的。
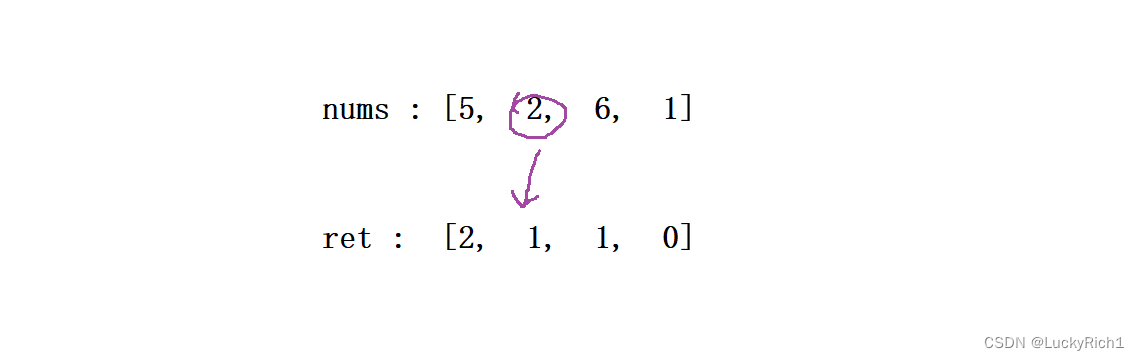
因此当算出nums[cur1]右边有多少个比我小的时候,最终加的结果是这个值对应的原始下标对应的值 += right - cur2 + 1。
所以我们着重要解决的问题是,当我们找到当前位置的值右边有多少个比我小的时候,我要能找到这个值得原始下标。 找到 nums 中当前元素的原始下标是多少? 因为排完序后原本数对应的下标就已经乱了!当前位置cur1 可能并不是我真实的下标。
可能你会想到用哈希表,但是,如果数组里面有重复元素,就难搞了。所以我们直接搞一下和原始数组大小的index数组,记录当前元素的原始下标。不管nums里面怎么办,就把index和nums里面对应的值绑定!nums里面的值动,index里面的值也动! 这样就可以通过index里面值找到当前值原始下标在哪里,然后就可以加了。

回归上面的问题 把nums[cur1] 对应的 index(下标) 里面的 ret += right - cur2 +1 就可以变成这样 ret[index[cur1]] += ret += right - cur2 +1。
当归并排序移动nums时,我们要合并两个有序数组,别忘记我们需要一个tmp辅助数组帮助我们合并。那如何让nums合并,index也同步绑定呢? 因此需要两个tmp辅助数组!
class Solution {
vector<int> ret;
vector<int> tmpNum;
vector<int> tmpIndex;
vector<int> index; // 记录 nums 中当前元素的原始下标
public:
vector<int> countSmaller(vector<int>& nums) {
int n = nums.size();
ret.resize(n);
tmpNum.resize(n);
tmpIndex.resize(n);
index.resize(n);
for(int i = 0; i < n; ++i) index[i] = i; // 初始化 index 数组
Mergesort(nums, 0, n - 1);
return ret;
}
void Mergesort(vector<int>& nums, int left, int right)
{
if(left >= right) return;
// 1. 根据中间点,划分区间
int mid = left + (right - left) / 2;
//[left, mid] [mid+1, right]
// 2. 先处理左右两部分
Mergesort(nums, left, mid);
Mergesort(nums, mid + 1, right);
// 3. 处理一左一右的情况
int cur1 = left, cur2 = mid + 1, i = 0;
while(cur1 <= mid && cur2 <= right) // 降序
{
if(nums[cur1] <= nums[cur2])
{
tmpNum[i] = nums[cur2];
tmpIndex[i++] = index[cur2++];
}
else
{
ret[index[cur1]] += right - cur2 + 1;
tmpNum[i] = nums[cur1];
tmpIndex[i++] = index[cur1++];
}
}
// 4.处理剩下排序过程
while(cur1 <= mid)
{
tmpNum[i] = nums[cur1];
tmpIndex[i++] = index[cur1++];
}
while(cur2 <= right)
{
tmpNum[i] = nums[cur2];
tmpIndex[i++] = index[cur2++];
}
for(int i = left; i <= right; ++i)
{
nums[i] = tmpNum[i - left];
index[i] = tmpIndex[i- left];
}
}
};
4.翻转对
题目链接:493. 翻转对
题目分析:
当 i < j 且 nums[i] > 2*nums[j],才是翻转对。
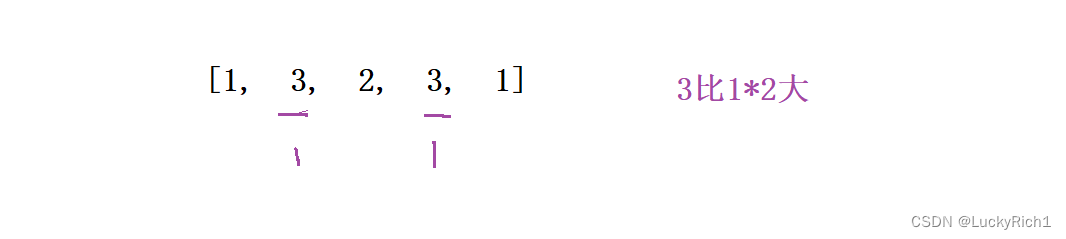
算法原理:
解法:分治
这个问题你会发现和求逆序对非常相似的,想求整个数组的翻转对,先求左半部分的翻转对记为a,在求右半部分的翻转对记为b,然后求一左一右的翻转对记为c。a+b+c就是整个数组的翻转对。
这个就有个致命的问题,逆序对的题和归并排序完美契合,仅需比较
i < j,nums[i] > nums[j] 。但是这道题要比较的是 i < j,nums[i] > 2 * nums[j]。这个时候就不能按照归并排序的流程求翻转对了,我们要重新想一个策略来求翻转对。
我们依旧用的是分治的策略来解决,但是并不是用的是归并排序里面的一个过程来解决我们的问题,我们是在归并排序之前来计算翻转对个数。因为我们要利用两个区间有序的性质,我们可以在一次归并中用O(N)的时间复杂度搞定这一层的翻转对的个数
计算翻转对
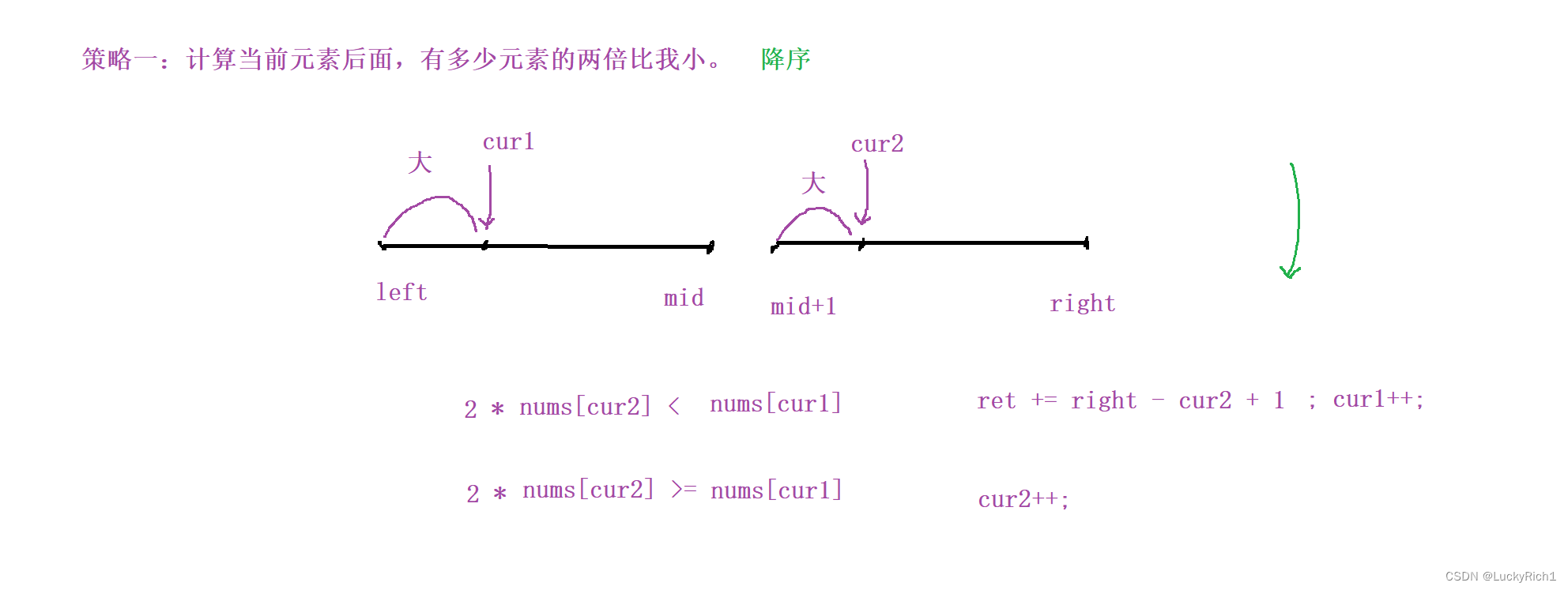
策略一:计算当前元素后面,有多少元素的两倍比我小。 降序
固定cur1
整个数组都是降序的,固定cur1,当 2 * nums[cur2] >= nums[cur1] cur2往后移,
当 2 * nums[cur2] < nums[cur1] ,因为是降序的,cur2后面一堆元素2倍都比cur1小,所以 ret += right - cur2 +1, cur1的翻转对都找完了所以往后移动就行了。注意cur2此时是不用回溯的!因为数组是降序的,cur2之前的元素都比cur1还没有移动的2倍大,cur1往后走一步元素变小了,那cur2之前不就比当前cur1位置更大嘛,所以不用回溯,如果回溯时间复杂度 计算翻转对就是O(n^2),那整体时间复杂度就变成O(n ^2 logn)。直到cur1到尾或者cur2到尾就结束了。
计算翻转对:利用单调性,使用同向双指针。
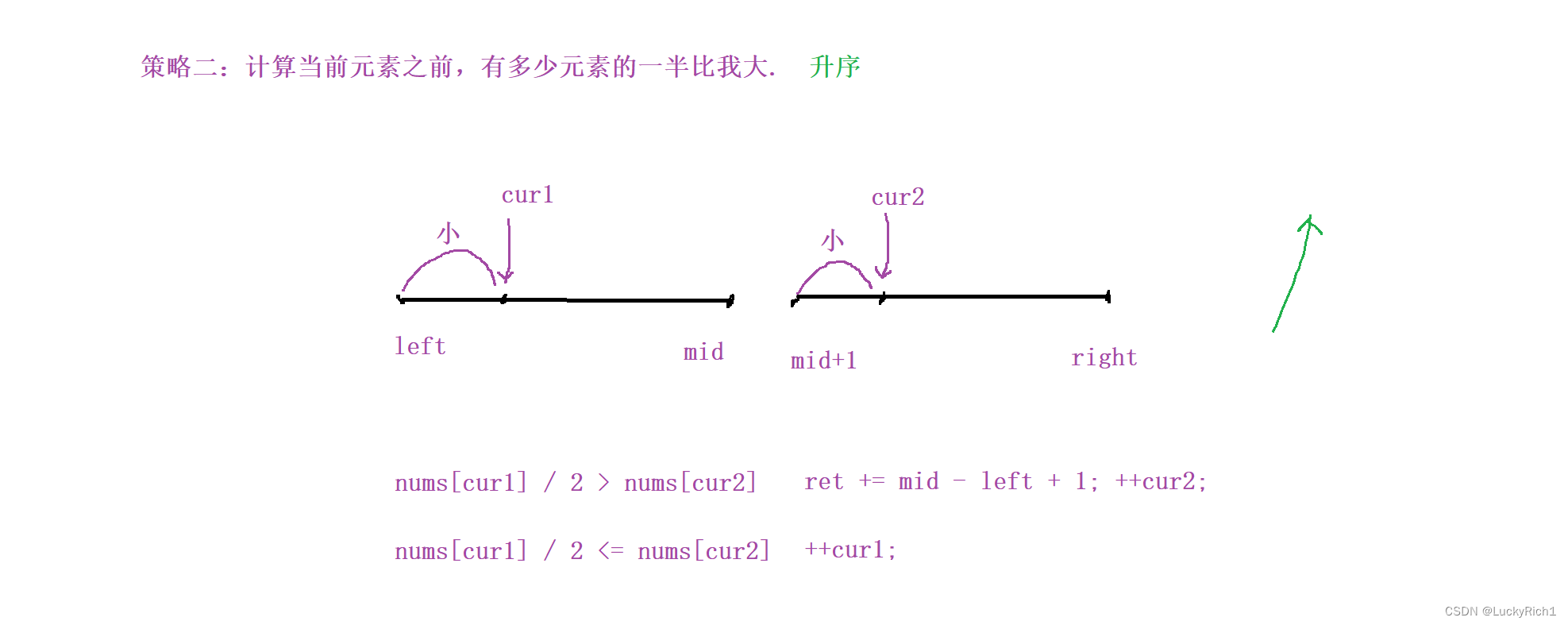
策略二:计算当前元素之前,有多少元素的一半比我大。 升序
固定cur2
整个数组都是升序的,固定cur2,当 nums[cur1] / 2 <= nums[cur1] cur1往后移,
当 nums[cur1] / 2 > nums[cur2] ,因为是升序的,cur1后面一堆元素的一半都比cur2大,所以 ret += mid - left +1, cur2的翻转对都找完了所以往后移动就行了。此时cur1也不需要回溯。因为是数组是升序的,cur2往后走一步是变大的,cur1还没有往后移动之前前面的元素一半都比cur2小,现在cur往后走一步变大,肯定比cur1还没有往后移动之前更大,所以cur1不需要回溯。
注意上面只是计算翻转对,别忘记还要还要合并两个有序数组。
降序
class Solution {
vector<int> tmp;
public:
int reversePairs(vector<int>& nums) {
int n = nums.size();
tmp.resize(n);
return Mergesort(nums, 0, n - 1);
}
int Mergesort(vector<int>& nums, int left, int right)
{
if(left >= right) return 0;
int ret = 0;
// 1. 选择中间点将数组划分区间
int mid = (left + right) >> 1;
// 2. 先计算左右两侧的翻转对
ret += Mergesort(nums, left, mid);
ret += Mergesort(nums, mid + 1, right);
// 3. 先计算翻转对的数量
int cur1 = left, cur2 = mid + 1;
while(cur1 <= mid && cur2 <= right)//降序
{
//if(2 * nums[cur2] < nums[cur1]) //乘法溢出 改成 除法
if(nums[cur2] < nums[cur1] / 2.0)
{
ret += right - cur2 + 1;
cur1++;
}
else
cur2++;
}
// 4. 合并两个有序数组
cur1 = left, cur2 = mid + 1;
int i = left;
while(cur1 <= mid && cur2 <= right)
{
if(nums[cur2] < nums[cur1]) tmp[i++] = nums[cur++];
else tmp[i++] = nums[cur2++];
}
while(cur1 <= mid) tmp[i++] = nums[cur1++];
while(cur2 <= right) tmp[i++] = nums[cur2++];
for(int j = left; j <= right; ++j) nums[j] = tmp[j];
return ret;
}
};
升序
class Solution {
vector<int> tmp;
public:
int reversePairs(vector<int>& nums) {
int n = nums.size();
tmp.resize(n);
return Mergesort(nums, 0, n - 1);
}
int Mergesort(vector<int>& nums, int left, int right)
{
if(left >= right) return 0;
int ret = 0;
// 1. 选择中间点将数组划分区间
int mid = (left + right) >> 1;
// 2. 先计算左右两侧的翻转对
ret += Mergesort(nums, left, mid);
ret += Mergesort(nums, mid + 1, right);
// 3. 先计算翻转对的数量
int cur1 = left, cur2 = mid + 1;
while(cur1 <= mid && cur2 <= right)//升序
{
//if(2 * nums[cur2] < nums[cur1]) //乘法溢出 改成 除法
if(nums[cur2] < nums[cur1] / 2.0)
{
ret += mid - cur1 + 1;
cur2++;
}
else
cur1++;
}
// 4. 合并两个有序数组
cur1 = left, cur2 = mid + 1;
int i = left;
while(cur1 <= mid && cur2 <= right)
{
if(nums[cur2] < nums[cur1]) tmp[i++] = nums[cur2++];
else tmp[i++] = nums[cur1++];
}
while(cur1 <= mid) tmp[i++] = nums[cur1++];
while(cur2 <= right) tmp[i++] = nums[cur2++];
for(int j = left; j <= right; ++j) nums[j] = tmp[j];
return ret;
}
};