往期文章请点这里
目录
- Vector Space Models
- Word by Word and Word by Doc
- Word by Document Design
- Word by Document Design
- Vector Space
- Euclidean Distance
- Euclidean distance for n-dimensional vectors
- Euclidean distance in Python
- Cosine Similarity: Intuition
- Cosine Similarity
- Previous definitions
- Cosine Similarity
- Manipulating Words in Vector Spaces
- Visualization and PCA
- Visualization of word vectors
- Principal Component Analysis
- PCA Algorithm
往期文章请点 这里
Vector Space Models
在实际生活中,经常会出现以下两种场景:
相同文字不同含义:
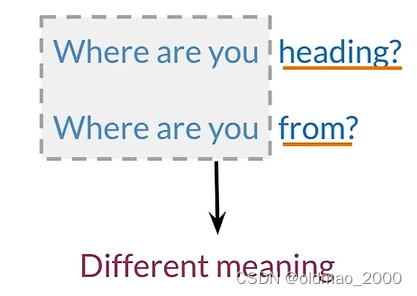
不同文字相同含义:

这些是之前的语言模型无法处理的问题,而向量空间模型不但可以区分以上场景,还能捕获单词之间的依赖关系。
You eat cereal from a bowl
麦片和碗是强相关
You buy something and someone else sells it
这里的买依赖于卖
这个优点使得向量空间模型可以用于下面任务:
著名语言学学者(Firth, J. R. 1957:11)说过:
“You shall know a word by the company it keeps”
指出了上下文对当前词的表达有很大影响。
Word by Word and Word by Doc
构建共现矩阵(W/W and W/D 两种),并为语料库的单词提取向量表示。
Word by Document Design
两个不同单词的共现是它们在语料库中在一个特定的词距内一起出现的次数。
Number of times they occur together within a certain distance
k
k
k
例如,假设语料库有以下两个句子。

假设
k
=
2
k=2
k=2,则单词data的共现次数如下:
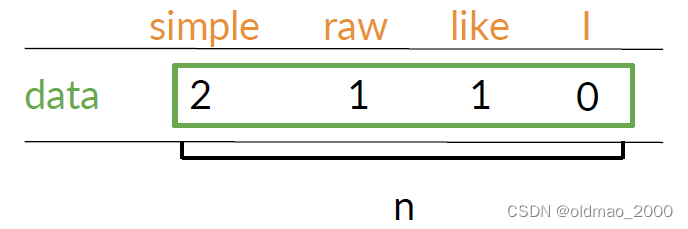
这里n取值在1到词表大小之间。data和simple在第一句话距离是1,第二句话距离是2:

Word by Document Design
计算来自词汇表的单词在属于特定类别的文档中出现的次数。
Number of times a word occurs within a certain category
例如下图中,语料库包含三类文档,然后可以计算某个单词分别在三类文档中出现的次数。
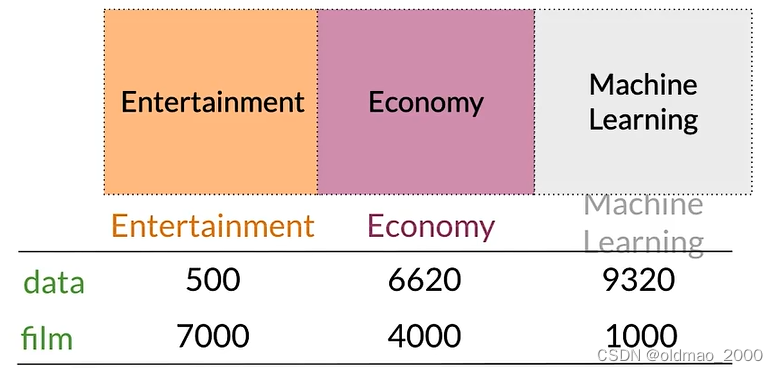
Vector Space
完成多组文档或单词的表示后,接下来可以构建向量空间。
以上面的矩阵为例

可以用行来表示单词,列表示文档,若以data和film构建坐标系,则可以根据矩阵中的数值得到向量表示:
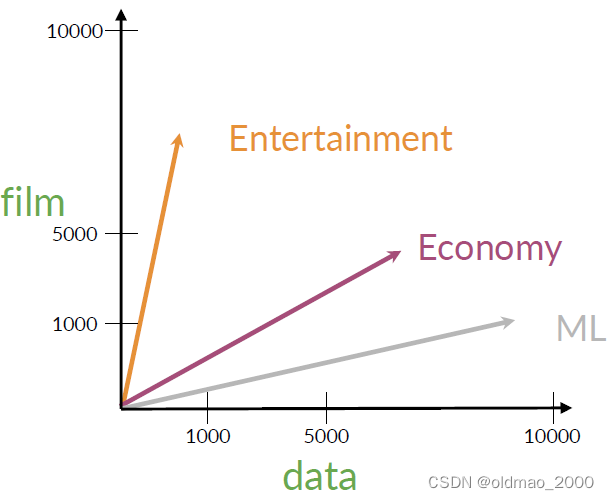
从向量空间表示中可以看到,economy的ML的文档相似度要更大一些
当然这个相似度可以用计算Angle Distance来数字化度量。
Euclidean Distance
Euclidean Distance允许我们确定两个点或两个向量彼此之间的距离。
书接上回,假设有两个语料的向量表示为:

放到二维空间中:
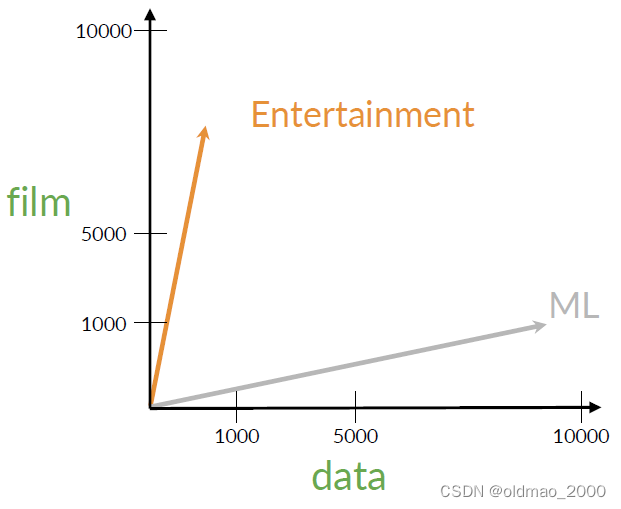
用点表示他们后,可以用欧氏距离很衡量二者的相似度:
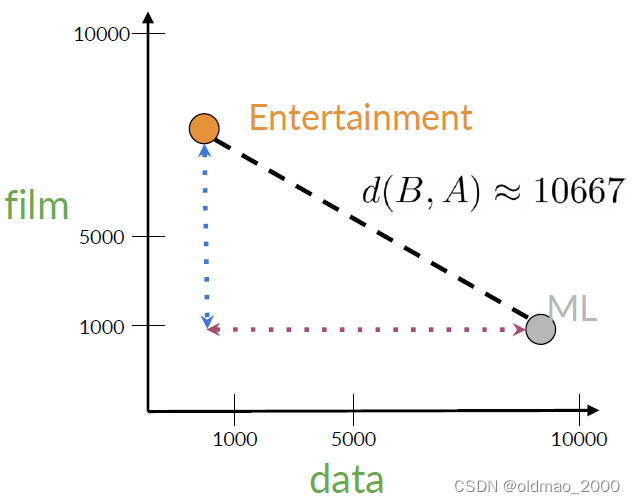
具体公式:
d
(
B
,
A
)
=
(
B
1
−
A
1
)
2
+
(
B
2
−
A
2
)
2
d(B,A)=\sqrt{(B_1-A_1)^2+(B_2-A_2)^2}
d(B,A)=(B1−A1)2+(B2−A2)2
B
1
−
A
1
B_1-A_1
B1−A1和
B
2
−
A
2
B_2-A_2
B2−A2分别对应上图中水平和垂直距离。
本例中带入数字:
d
(
B
,
A
)
=
(
−
8820
)
2
+
(
6000
)
2
≈
10667
d(B,A)=\sqrt{(-8820)^2+(6000)^2}\approx10667
d(B,A)=(−8820)2+(6000)2≈10667
Euclidean distance for n-dimensional vectors
对于高维向量,欧氏距离仍然适用,例如:
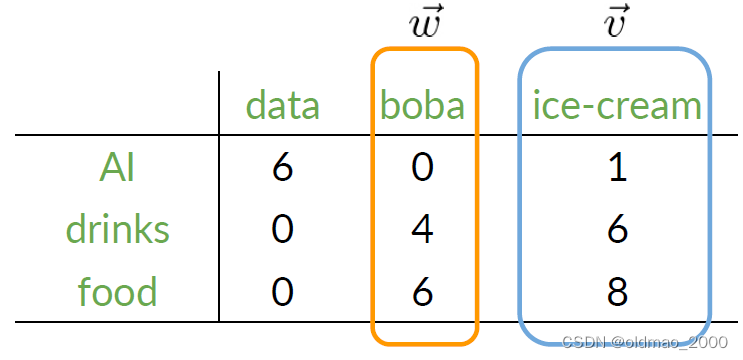
想要计算ice-cream和boba的欧氏距离,则可以使用以下公式:
d
(
v
⃗
,
w
⃗
)
=
∑
i
=
1
n
(
v
i
−
w
i
)
2
等价于求范数Norm of
(
v
⃗
,
w
⃗
)
d(\vec{v},\vec{w})=\sqrt{\sum_{i=1}^n(v_i-w_i)^2}等价于求范数\text{Norm of}(\vec{v},\vec{w})
d(v,w)=i=1∑n(vi−wi)2等价于求范数Norm of(v,w)
ice-cream和boba的欧氏距离可以写为:
(
1
−
0
)
2
+
(
6
−
4
)
2
+
(
8
−
6
)
2
=
1
+
4
+
4
=
3
\sqrt{(1-0)^2+(6-4)^2+(8-6)^2}=\sqrt{1+4+4}=3
(1−0)2+(6−4)2+(8−6)2=1+4+4=3
Euclidean distance in Python
在这里插入代码片
# Create numpy vectors v and w
v np. array([1, 6, 8])
w np. array([0, 4, 6])
# Calculate the Euclidean distance d
d = np.linalg.norm(v-w)
# Print the result
print (("The Euclidean distance between v and w is: ", d)
Cosine Similarity: Intuition
先给结论:当语料库中文章包含单词数量差异较大时,使用Cosine Similarity
余弦相似度使用文档之间的角度,因此不依赖于语料库的大小。
假设我们有eggs和disease两个单词在三个语料库中图像如下:
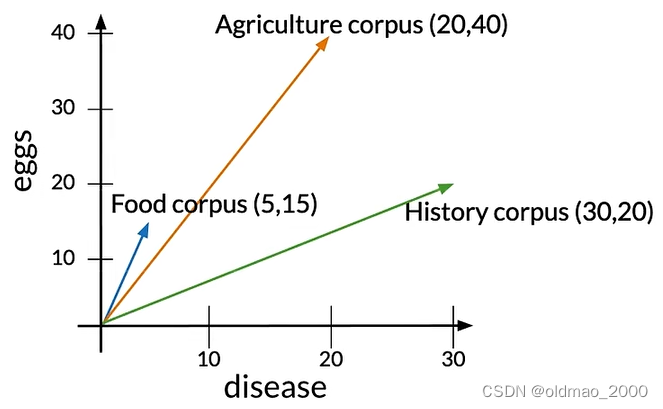
语料库中各个类型的文章单词数量不相同,这里的Agriculture和History文章单词数量基本相同,而Food文章单词较少。Agriculture与其他两类文章的欧式距离分别写为:
d
1
d_1
d1和
d
2
d_2
d2
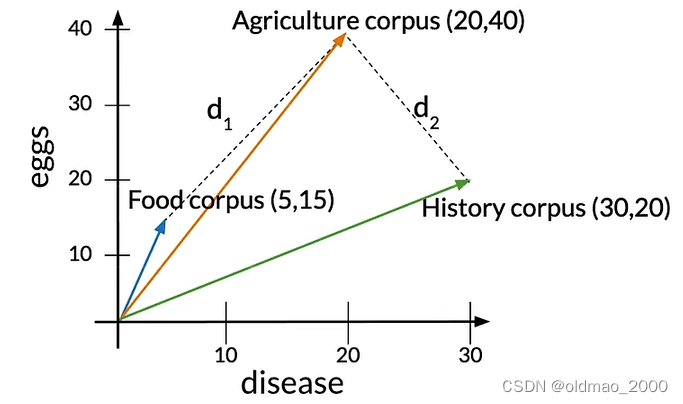
从图中可以看到
d
2
<
d
1
d_2<d_1
d2<d1,表示Agriculture和History文章相似度更高。
余弦相似度是指The cosine of the angle between the vectors. 当角度接近90度时,余弦接近于0。
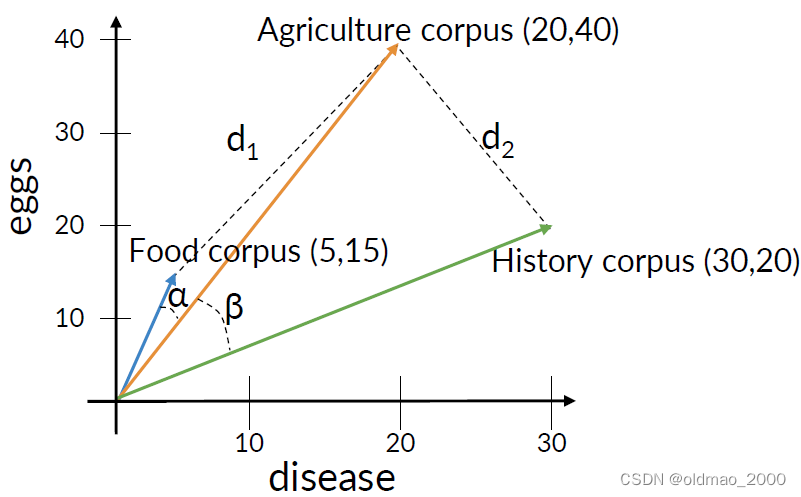
从余弦相似度上看,
β
>
α
\beta>\alpha
β>α,表示Agriculture和Food文章相似度更高。
Cosine Similarity
Previous definitions
先回顾两个定义:
Vector norm,向量的模(范数)可以表示为:
∣
∣
v
⃗
∣
∣
=
∑
i
=
1
n
v
i
2
||\vec{v}||=\sqrt{\sum_{i=1}^nv_i^2}
∣∣v∣∣=i=1∑nvi2
Dot product点乘可以表示为:
v
⃗
⋅
w
⃗
=
∑
i
=
1
n
v
i
⋅
w
i
\vec{v}\cdot \vec{w}=\sum_{i=1}^nv_i\cdot w_i
v⋅w=i=1∑nvi⋅wi
下面是点乘推导:
设有两个向量
a
\mathbf{a}
a 和
b
\mathbf{b}
b,在
n
n
n维空间中的坐标分别为
(
a
1
,
a
2
,
…
,
a
n
)
(a_1, a_2, \ldots, a_n)
(a1,a2,…,an) 和
(
b
1
,
b
2
,
…
,
b
n
)
(b_1, b_2, \ldots, b_n)
(b1,b2,…,bn)。这两个向量的点积定义为:
a
⋅
b
=
a
1
b
1
+
a
2
b
2
+
…
+
a
n
b
n
\mathbf{a} \cdot \mathbf{b} = a_1b_1 + a_2b_2 + \ldots + a_nb_n
a⋅b=a1b1+a2b2+…+anbn
向量
a
\mathbf{a}
a 和
b
\mathbf{b}
b 的范数(长度)分别是:
∥
a
∥
=
a
1
2
+
a
2
2
+
…
+
a
n
2
\|\mathbf{a}\| = \sqrt{a_1^2 + a_2^2 + \ldots + a_n^2}
∥a∥=a12+a22+…+an2
∥
b
∥
=
b
1
2
+
b
2
2
+
…
+
b
n
2
\|\mathbf{b}\| = \sqrt{b_1^2 + b_2^2 + \ldots + b_n^2}
∥b∥=b12+b22+…+bn2
两个向量之间的夹角
θ
\theta
θ 的余弦值可以通过点积和范数来表示:
cos
(
θ
)
=
a
⋅
b
∥
a
∥
∥
b
∥
\cos(\theta) = \frac{\mathbf{a} \cdot \mathbf{b}}{\|\mathbf{a}\| \|\mathbf{b}\|}
cos(θ)=∥a∥∥b∥a⋅b
将点积的公式代入上述表达式,我们得到:
cos
(
θ
)
=
a
1
b
1
+
a
2
b
2
+
…
+
a
n
b
n
a
1
2
+
a
2
2
+
…
+
a
n
2
b
1
2
+
b
2
2
+
…
+
b
n
2
\cos(\theta) = \frac{a_1b_1 + a_2b_2 + \ldots + a_nb_n}{\sqrt{a_1^2 + a_2^2 + \ldots + a_n^2} \sqrt{b_1^2 + b_2^2 + \ldots + b_n^2}}
cos(θ)=a12+a22+…+an2b12+b22+…+bn2a1b1+a2b2+…+anbn
如果我们将
cos
(
θ
)
\cos(\theta)
cos(θ) 乘以
a
\mathbf{a}
a 和
b
\mathbf{b}
b,我们可以得到点积的另一种形式:
∥
a
∥
∥
b
∥
cos
(
θ
)
=
a
1
b
1
+
a
2
b
2
+
…
+
a
n
b
n
=
a
⋅
b
\|\mathbf{a}\| \|\mathbf{b}\| \cos(\theta) = a_1b_1 + a_2b_2 + \ldots + a_nb_n=\mathbf{a} \cdot \mathbf{b}
∥a∥∥b∥cos(θ)=a1b1+a2b2+…+anbn=a⋅b
Cosine Similarity
下图是单词eggs和disease在语料Agriculture和History出现频率的可视化表达。

根据上面推导的公式:
v
^
⋅
w
^
=
∣
∣
v
^
∣
∣
∣
∣
w
^
∣
∣
cos
(
β
)
cos
(
β
)
=
v
^
⋅
w
^
∣
∣
v
^
∣
∣
∣
∣
w
^
∣
∣
=
(
20
×
30
)
+
40
×
20
2
0
2
+
4
0
2
×
3
0
2
+
2
0
2
=
0.87
\hat v\cdot\hat w =||\hat v||||\hat w||\cos(\beta)\\ \cos(\beta)=\cfrac{\hat v\cdot\hat w}{||\hat v||||\hat w||}\\ =\cfrac{(20\times30)+40\times20}{\sqrt{20^2+40^2}\times\sqrt{30^2+20^2}}=0.87
v^⋅w^=∣∣v^∣∣∣∣w^∣∣cos(β)cos(β)=∣∣v^∣∣∣∣w^∣∣v^⋅w^=202+402×302+202(20×30)+40×20=0.87
下面是余弦相似度的两个特殊情形:
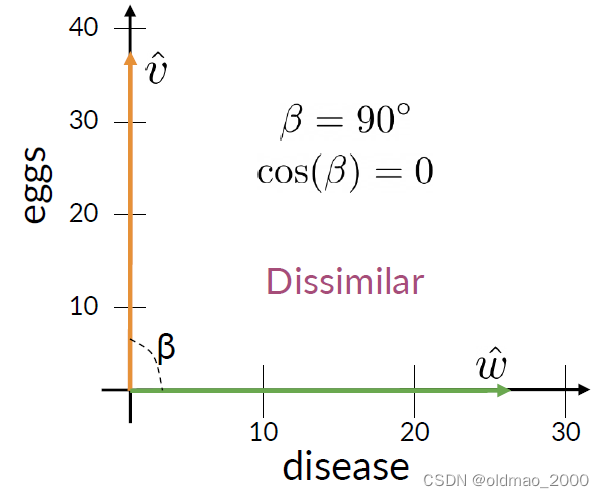
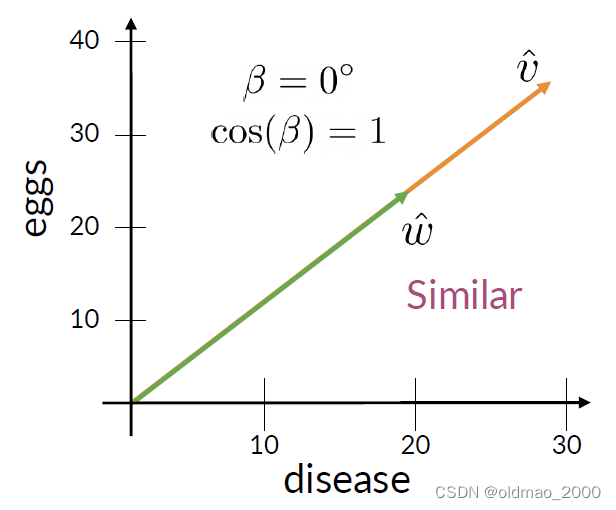
注意:
Cosine Similarity gives values between 0 and 1.
Manipulating Words in Vector Spaces
扩展阅读:[Mikolov et al, 2013, Distributed Representations of Words and Phrases and their Compositionality]
这里的Manipulating Words,是指对词向量的加减(平移向量),使得我们可以计算对应关系,例如:已有国家和首都的词向量空间,已知漂亮国首都是DC(漫威表示不服),求大毛的首都是什么。
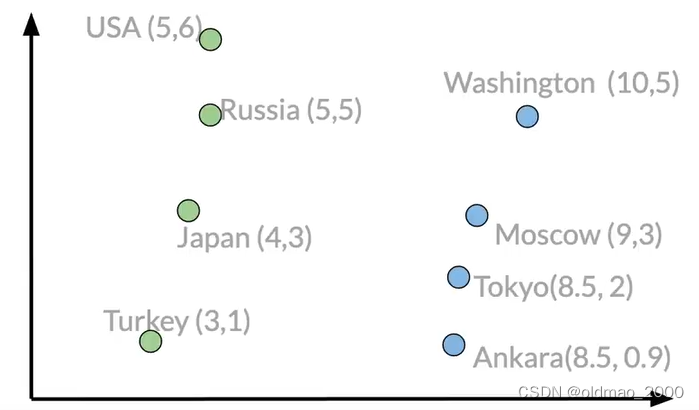
在本例子中,我们有一个假想的二维向量空间,里面包含了不同国家和首都的不同向量表示:
这里我们可以计算USA到Washington的向量差异(也相当于求USA到Washington之间的关系,也就是求连接二者的向量)
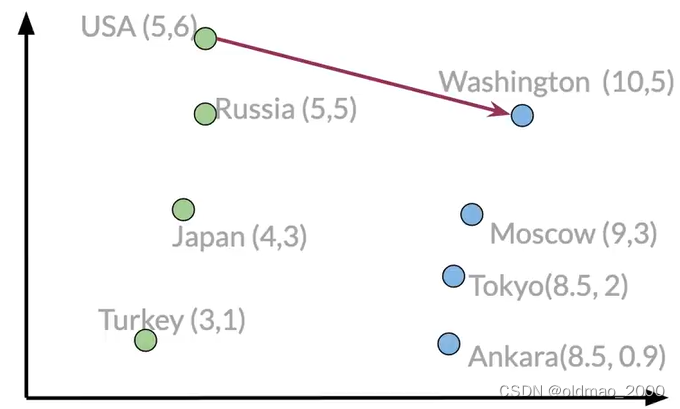
Washington-USA = [5 -1]
通过这个我们就可以知道要找到一个国家的首都需要移动多少距离,对于大毛就有:
Russia + [5 -1]=[10 4]
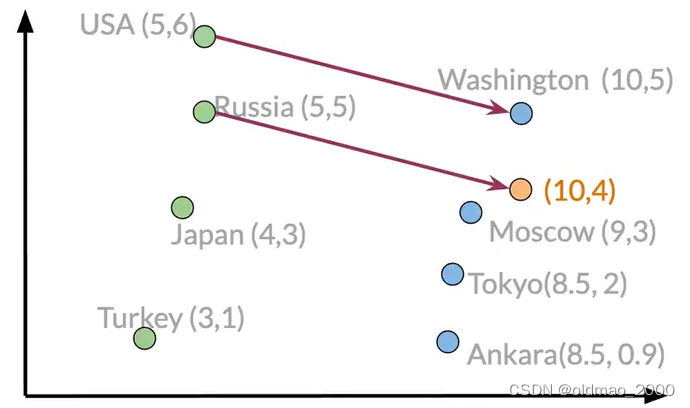
虽然[10 4]没有匹配到具体的城市,我们可以进一步比较每个城市的欧氏距离或者余弦相似性找到最邻近的城市。
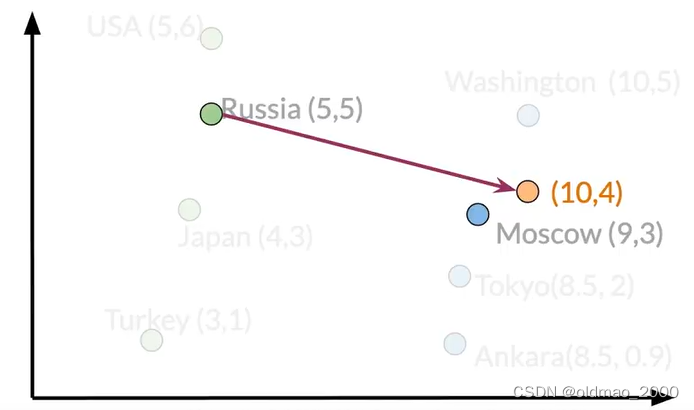
答案是:Moscow
Visualization and PCA
可视化可以让我们很直观的看到单词的相似性,当单词的向量表示通常是高维的,需要我们将其降维到2D空间便于绘图,这里先学其中一种降维写方式:PCA
Visualization of word vectors
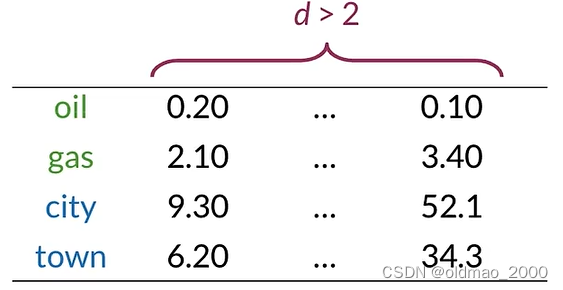
假设词向量维度远大于2,已知oil和gas,city和town相似度较高,如何可视化他们之间的关系?答案就是降维:
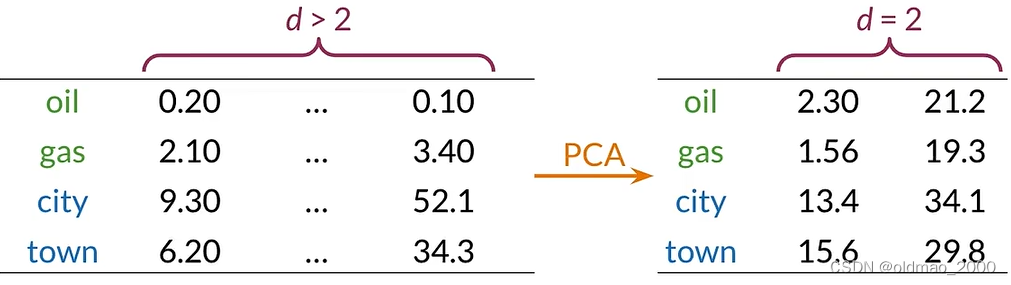
然后再进行可视化,则可得到类似下图的结果:
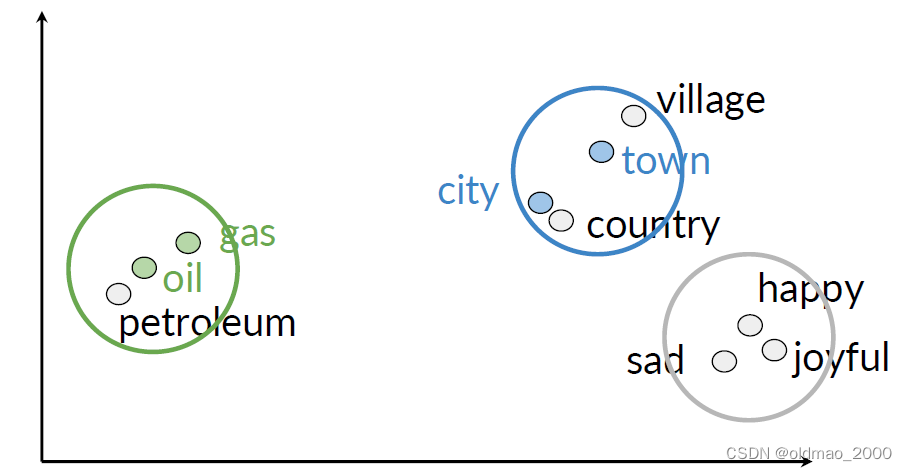
Principal Component Analysis
以二维空间为例来看:
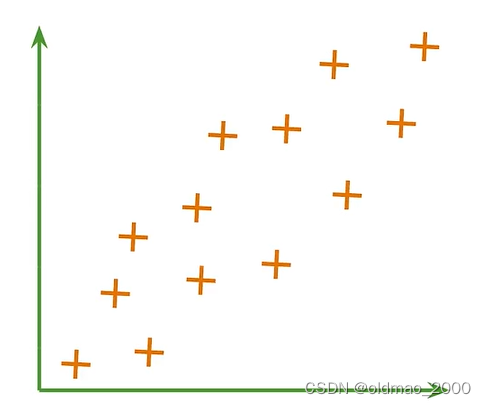
降维就是将Uncorrelated Features映射到另外一个维度空间,并尽量保留更多信息,二维的映射方式一眼就可以看出来,就是垂直映射:
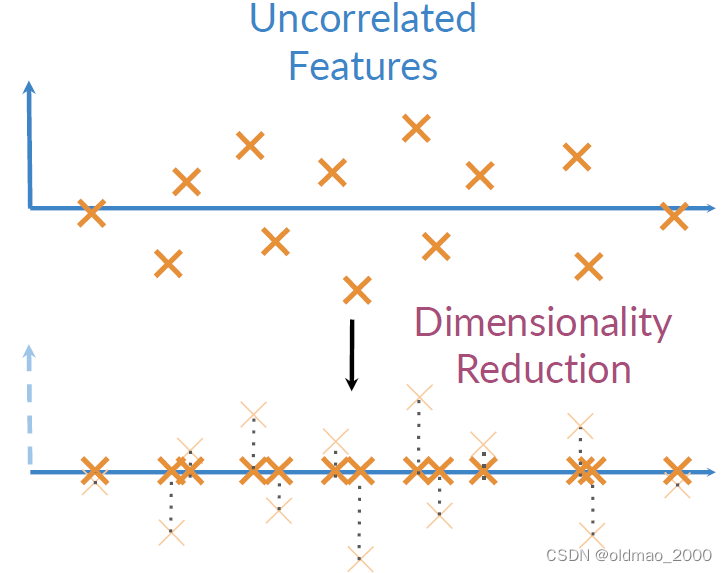
PCA Algorithm
在线代中有两个概念:Eigenvector(特征向量)和Eigenvalue(特征值)
特征值(Eigenvalue):
特征值是与线性变换相关联的一个标量,它描述了在该变换下,一个向量被缩放的比例。
对于一个给定的线性变换(由矩阵表示),如果存在一个非零向量
v
v
v,使得变换后的向量与原向量成比例,即
A
v
=
λ
v
Av=\lambda v
Av=λv,其中
A
A
A 是矩阵,
λ
\lambda
λ 是一个标量,那么
λ
\lambda
λ 就是
A
A
A 的一个特征值,而
v
v
v 就是对应的特征向量。
特征向量(Eigenvector):
特征向量是线性变换下保持方向不变的向量,或者更准确地说,是方向被缩放的向量。
在上述方程
A
v
=
λ
v
Av=\lambda v
Av=λv 中,如果
λ
≠
0
\lambda\neq 0
λ=0,那么
v
v
v 就是
A
A
A 的一个特征向量,它与特征值
λ
\lambda
λ 配对出现。
不需要知道如何计算这两个东西
算法第一步是为这一步获取一组无关的特征,需要对数据进行归一化,然后计算方差矩阵。
Mean Normalize Data
x
i
=
x
i
−
μ
x
i
σ
x
i
\text{Mean Normalize Data }x_i=\cfrac{x_i-\mu_{x_i}}{\sigma_{x_i}}
Mean Normalize Data xi=σxixi−μxi
第二步计算方差矩阵(Get Covariance Matrix):
Σ
\Sigma
Σ
第三步奇异值分解(Perform SVD)得到一组三个矩阵:
S
V
D
(
Σ
)
SVD(\Sigma)
SVD(Σ)
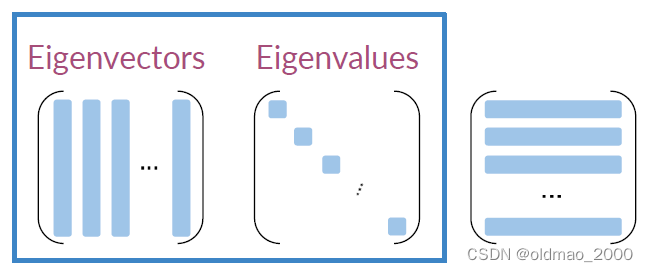
SVD可以直接调用函数解决不用搓轮子。
然后进行投影,将Eigenvector(特征向量)和Eigenvalue(特征值)分别记为
U
U
U和
S
S
S
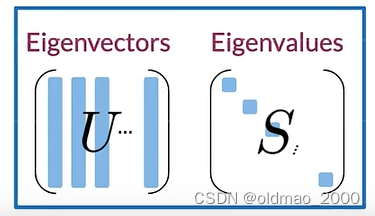
然后通过X点积U的前面两列来投影数据,这里我们只保留两列以形成二维可视化空间:
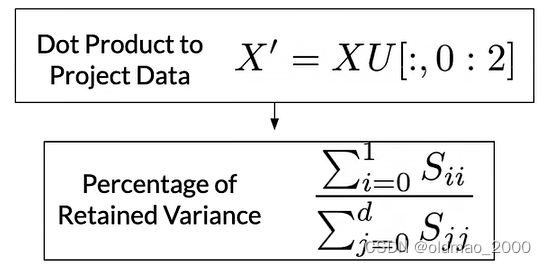
Percentage of Retained Variance: 这表示保留的方差百分比。在PCA中,我们通常选择前几个主成分来近似原始数据,这些主成分加起来解释了原始数据的一定比例的方差。