目录
Propensity Score
Propensity Score Estimation
Propensity Score and ML
Propensity Score and Orthogonalization
Propensity Score
倾向加权法围绕倾向得分的概念展开,其本身源于这样一种认识,即不需要直接控制混杂因素 X 来实现条件独立性 。相反,只需控制一个估计
的平衡分值即可。这个平衡分数通常就是干预的条件概率
,也称为倾向分数
。
倾向得分可视为一种降维技术。X 的维度可能非常高,与其以 X 为条件,不如直接以倾向得分为条件,以阻止流经 X 的后门路径: 。
这有一个正式的证明。这并不复杂,但有点超出本书的范围。在这里,你可以用更直观的方法来解决这个问题。倾向得分是接受干预的条件概率,对吗?因此,你可以把它看成是某种将 X 转化为干预 T 的函数。倾向得分是变量 X 和干预 T 之间的中间值:这就是它在因果图中的样子:
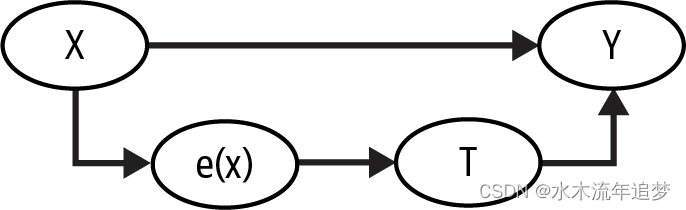
在这张图中,如果你知道 是什么,那么仅凭 X 就无法进一步了解 T 的信息。这意味着,控制
与直接控制 X 的效果是一样的。
从经理培训计划的角度来考虑。接受培训的经理和未接受培训的经理最初并不具有可比性,因为直接下属参与度更高的经理更有可能参加培训。但是,如果取两个经理,一个来自干预组,一个来自对照组,但接受干预的概率相同,他们就具有可比性了。想想看。如果他们接受干预的概率完全相同,那么其中一个接受干预而另一个没有接受干预的唯一原因就是纯属偶然。在倾向得分相同的情况下,干预与随机一样好。
Propensity Score Estimation
在理想情况下,您会得到真实倾向得分 。 在条件随机实验中,分配机制是非确定的,但却是已知的。然而,在大多数情况下,分配干预的机制是未知的,您需要用
的估计值来替代真实倾向得分。
既然是二元干预,那么估计 的最佳方法就是使用逻辑回归。要使用 statsmodels 拟合 logistic 回归,只需将方法 ols 改为 logit 即可:
ps_model = smf.logit("""intervention ~
tenure + last_engagement_score + department_score
+ C(n_of_reports) + C(gender) + C(role)""", data=df).fit(disp=0)将估计的倾向分数保存在数据框架中;在接下来的章节中,你会经常用到它,我将向你展示如何使用它以及它的作用:
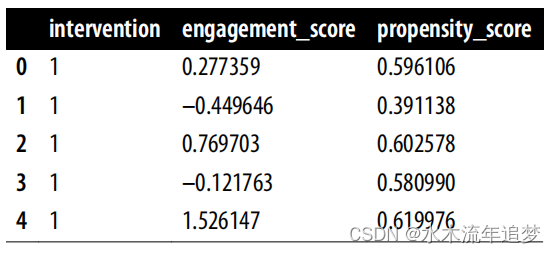
data_ps = df.assign(
propensity_score = ps_model.predict(df),
)
data_ps[["intervention", "engagement_score", "propensity_score"]].head()Propensity Score and ML
另外,您也可以使用机器学习模型来估算倾向得分。但这需要您更加谨慎。首先,您必须确保机器学习模型输出的是经过校准的概率预测。其次,您需要使用折外预测,以避免过度拟合造成的偏差。您可以使用 sklearn 的校准模块来完成第一项任务,使用模型选择模块中的 cross_val_predict 函数来完成后一项任务。
Propensity Score and Orthogonalization
如果您还记得上一章的内容,根据 FLW 定理,线性回归也做了与倾向得分估计非常相似的事情。因此,与倾向得分估计非常相似,OLS 也在对治疗分配机制进行建模。这意味着您也可以在线性回归中使用倾向得分 来调整混杂因素 X:
model = smf.ols("engagement_score ~ intervention + propensity_score",
data=data_ps).fit()
model.params["intervention"]
0.26331267490277066用这种方法得到的 ATE 估计值与之前用干预和混杂因素 X 拟合线性模型得到的 ATE 估计值非常相似。唯一不同的是,OLS 使用线性回归对 T 进行建模,而该倾向得分估计值是通过逻辑回归得到的。