高级计算机体系结构--三次作业

homework1
homework2
homework3

homework1

简述 当代主流的并行机系统。

【答】

当代并行机系统主要有：

1）并行向量机（PVP）

2）对称多处理机（SMP）

3）大规模并行处理机（MPP）

4）分布式共享存储（DSM）处理机

5）工作站机群（COW）

简述 并行计算机的主要访存模型。

【答】

1）均匀存储访问模型（UMA）

2）非均匀存储访问模型（NUMA）

3）全高速缓存存储访问模型（COMA）

4）高速缓存一致性非均匀访问模型（CC-NUMA）

5）非远程存储访问模型（NORMA）

使用 4GHZ 主频的标量处理器执行一个典型测试程序，其所执行的指令数及所需的周期数如下表所示。试 计算执行该程序的有效 CPI、MIPS 速率及总的 CPU 执行时间。

指令类型	指令数	时钟周期数
整数算术	45,000	1
数据传送	32,000	2
浮点	15,000	2
控制转移	8,000	2

【解】

$\frac{执行整个程序所需的时钟周期数}{程序中指令总数}$ ，即：

$\begin{aligned}\\ CPI &= \frac{\sum_{i=1}^n(CPI_i \times I_i)}{I_N} \\\\ &= \frac{45000 \times 1+32000 \times 2+15000 \times 2+ 8000 \times 2}{45000+32000+15000+8000} \\\\ &= 1.55\\ \end{aligned}$

时钟频率 $R_C$ 为 $4GHz=4\times10^9Hz$ ， $M I PS$ （每秒百万条指令）为：

$\begin{aligned}\\ MIPS &= \frac{R_C}{CPI \times 10^6} \\\\ &= \frac{4 \times 10^9}{1.55\times10^6} \\\\ &= 2580.7\\ \end{aligned}$

$\times 时钟周期 = \frac{总时钟周期数}{时钟频率}$ ，即：

$\begin{aligned}\\ T_{CPU} &= \frac{T_C}{R_C} \\\\ &= \frac{45000 \times 1+32000 \times 2+15000 \times 2+ 8000 \times 2}{4\times10^9} \\\\ &= 3.875\times10^{-5}s\\ \end{aligned}$

欲在 4GHZ 主频的标量处理器上执行20万条目标代码指令程序。假定该程序中含有4种主要类型之指令，各指令所占的比例及 CPI 数如下表所示，试计算：

①在 单处理机上执行该程序的平均 CPI。

②由①所得结果，计算相应的 MIPS 速率。

指令类型	CPI	指令所占比例
ALU	1	60%
LOAD/STORE（高速缓存命中）	2	18%
分支	4	12%
访存（高速缓存缺失）	8	10%

【解】

（1）

$\begin{aligned}\\ CPI &= 1 \times 60\% + 2 \times 18\% + 4 \times 12\% + 8 \times 10\% \\\\ &= 2.24\\ \end{aligned}$

（2）

$\begin{aligned}\\ MIPS &= \frac{R_C}{CPI \times 10^6} \\\\ &= \frac{4\times10^9}{2.24\times10^6} \\\\ &= 1785.7\\ \end{aligned}$

已知 SP2 并行计算机的通信开销表达式 $t (m) = 46 + (0.035) m$ ，计算 渐进带宽和半峰值信息长度，提示 $t_0=46us$ 。

【答】

渐进带宽 $r_{\infty}=\frac{1}{0.035}=28.6 \ MB/s$

半峰值信息长度 $m_{\frac{1}{2}}=t_0\times r_{\infty}=46us \times 28.6MB/s=1315.6B$

为什么增加问题规模可以在一定程度提高 加速比？

【答】

1）较大的问题规模可提高较大的并发度。

2）额外开销的增加可能慢于有效计算的增加。

3）算法中的串行分量比例不是固定不变的（串行部分所占的比例随着问题规模的增大而缩小）。

请简要描述以下共享存储并行代码中为何需要三次 Barrier？如何改进。

在这里插入图片描述

【答】

代码中的 barrier 函数调用是同步点，每个 barrier 都是必要的，它们确保了在关键的计算步骤之间所有线程的同步，防止数据冲突和不一致的结果。

第一次 barrier 用于等待所有线程都完成初始化，确保全局变量 diff 在 for 循环计算之前为 0.f。
第二次 barrier 用于等待所有线程都累加到全局变量 diff ，每一轮迭代中，diff 是所有线程的 myDiff 变量之和。
第三次 barrier 用于等待所有线程检查是否满足了收敛条件，确保每个线程对全局变量 done 的操作相同。

通过在连续的循环迭代中使用不同的 $d i ff$ 变量来删除依赖关系，权衡占用空间以消除依赖关系（一种常见的并行计算技巧）。

改进如下：

int n; // grid size
bool done = false;
LOCK myLock;
BARRIER myBarrier;
float diff[3]; // global diff, but now 3 copies

float *A = allocate(n+2, n+2);

void solve(float* A) {
 float myDiff; // thread local variable
 int index = 0; // thread local variable
 
 diff[0] = 0.0f;
 barrier(myBarrier, NUM_PROCESSORS); // one-time only: just for init
 
 while (!done) {
	 myDiff = 0.0f;
	 // 这里不再需要 barrier 确保全局 diff 初始化为 0.f
	 
	 //
	 // perform computation (accumulate locally into myDiff)
	 //
	 lock(myLock);
	 diff[index] += myDiff; // atomically update global diff
	 unlock(myLock);
	 diff[(index+1) % 3] = 0.0f;
	 barrier(myBarrier, NUM_PROCESSORS);  
	 // 这个barrier既等待全局diff[index]的值，又初始化全局diff[(index+1)%3]的值为0.f
	 
	 if (diff[index]/(n*n) < TOLERANCE)  
		 break;
	 // 这里不再需要barrier确保各线程对全局done进行相同操作，直接break
	 index = (index + 1) % 3;
 }
}

homework2

修改课本中的 基本路由器模型，使其只使用输入缓冲并且没有虚通道。针对该路由器模型，重写虫孔交换和报文交换的基本延迟表达式。

【答】

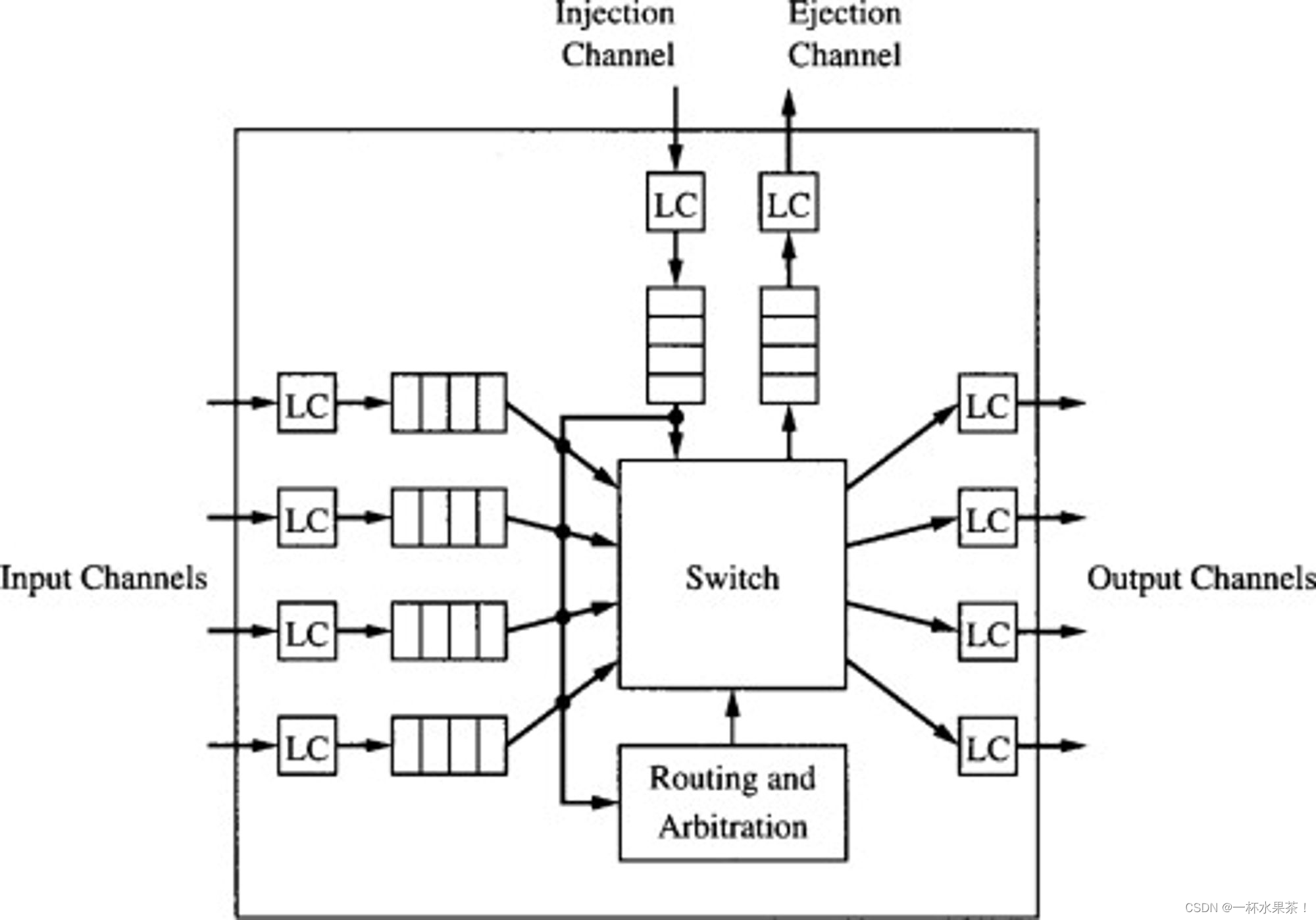
在这里插入图片描述

基本延迟表达式如下，

$\begin{aligned}\\ t_{虫孔} &= D(t_r+t_s+t_w)+(t_s+t_w)⌈\frac{L}{W}⌉ \\\\ t_{报文} &= D[t_r+(t_s+t_w)⌈\frac{L+W}{W}⌉]\\ \end{aligned}$

写出二维网格中 最小北最后算法。

算法：二维网格中最小北向最后算法
输入：当前节点的坐标(Xcurrent,Ycurrent)和目标节点的坐标(Xdest,Ydest)
输出：选择的输出通道Channel
过程：
   Xoffest := Xdest - Xcurrent;
   Yoffset := Ydest - Ycurrernt;
   
   If Xoffset < 0 and Yoffset >= 0 then 
     Channel := X-;
   endif
   
   If Xoffset < 0 and Yoffset < 0 then
     Channel := Select (X-, Y-);  // Select 选择函数，从通道中选择一个空闲的通道
   endif
   
   If Xoffset › 0 and Yoffset >= 0 then
     Channel := X+;
   endif
   
   if Xoffset > 0 and Yoffset < 0 then
     Channel := Select (X+, Y-);
   endif
   
   If Xoffset = 0 and Yoffset > 0 then
     Channel := Y+;
   endif
   
   if Xoffset = 0 and Yoffset < 0 then
     Channel := Y-;
   endif
   
   If Xoffset = 0 and Yoffset = 0 then 
     Channel := Internal;  // Internal 是连接本地节点的通道
   endif

采用 转弯模型，针对 三维网格给出最短路径部分自适应路由算法，使这些算法具有尽可能少的路由限制。

算法：三维网格最短路径部分自适应路由算法
输入：当前节点坐标（Xcurrent,Ycurrent,Zcurrent）和目的节点坐标（Xdest,Ydest,Zdest）
输出：选择的输出通道Channel
过程：
Xoffset := Xdest - Xcurrent;
Yoffset := Ydest - Ycurrent;
Zoffset := Zdest - Zcurrent;
if (Xoffset && Yoffset && Zoffset){
   随机选取第S维
   while(Soffset > 0) Channel := S+;
   while(Soffset < 0) Channel := S-;
   在剩下的二维平面中做西向优先路由;
} else
   存在第S维，使 Soffset = 0 成立,在剩下的二维平面中做西向优先路由;
RETURN;

给出 蝶式 MIN 中可以建立 无冲突路径的充要条件。

【答】

在蝶形 MIN 中， $t_i=d_{i+1}(0≤i≤n-2),t_{n-1}=d_0$ ，

如果要对于任意两个输入/输出对 $(S, D)$ 和 $(R, T)$ 建立无冲突的两条路径，其充要条件为：

对于任意的 $i$ 都有 $s_{n-1}s_{n-2}…s_{i+1}d_id_{i-1}d_{i-2}…d_2d_1d_{i+1}$ 不等于 $r_{n-1}r_{n-2}…r_{i+1}t_it_{i-1}t_{i-2}…t_2t_1t_{i+1}$ 。

给出 立方体网络中的自路由标记。

【答】

立方网络： $C_i$ 为第 $n - i$ 个蝶形排列（ $i = 1, 2, \dots, n$ ）， $C_0$ 为完全混洗排列。

考虑从 $S_{n-1}S_{n-2}…S_1S_0$ 到 $D_{n-1}D_{n-2}…D_1D_0$ 建立一条电路，

经过第 0 级链路： $S_{n-1}S_{n-2}…S_1S_0 \rightarrow S_{n-2}S_{n-3}…S_1S_0S_{n-1}$

作为第 0 级开关的输入地址，经过第 0 级开关 $S_{n-2}S_{n-3}…S_1S_0S_{n-1} \rightarrow S_{n-2}S_{n-3}…S_1S_0S_{n-1}^{’}$

经过第 1 级链路： $S_{n-2}S_{n-3}…S_1S_0S_{n-1}^{’} \rightarrow S_{n-1}^{’}S_{n-3}…S_1S_0S_{n-2}$

作为第 1 级开关的输入地址，经过第 1 级开关 $S_{n-1}^{’}S_{n-3}…S_1S_0S_{n-2} \rightarrow S_{n-1}^{’}S_{n-3}…S_1S_0S_{n-2}^{’}$

经过第 2 级链路： $S_{n-1}^{’}S_{n-3}…S_1S_0S_{n-2}^{’} \rightarrow S_{n-1}^{’}S_{n-2}^{’}… S_1S_0S_{n-3}$

作为第 2 级开关的输入地址，经过第 2 级开关 $S_{n-1}^{’}S_{n-2}^{’}… S_1S_0S_{n-3} \rightarrow S_{n-1}^{’}S_{n-2}^{’}… S_1S_0S_{n-3}^{’}$

类似的有第 $i$ 级开关的输出为 $S_{n-1}^{’}S_{n-2}^{’}…S_{n-i}^{’}S_{n-i-2}…S_1S_0S_{n-i-1} \rightarrow S_{n-1}^{’}S_{n-2}^{'}…S_{n-i}^{’}S_{n-i-2}…S_1S_0S_{n-i-1}^{’}$

从而第 $n - 1$ 级开关的输出为 $S_{n-1}^{’}S_{n-2}^{’}……S_1^{’}S_0^{’}$

最后一级连接为恒等排列，所以 $S_{n-1}^{’}S_{n-2}^{’}……S_1^{’}S_0^{’}=d_{n-1}d_{n-2}…d_1d_0$

从而有 $S_i^{’}=d_i$

所以第 $i$ 级开关的输出为 $d_{n-1}d_{n-2}…d_{n-i}S_{n-i-2}…S_1S_0d_{n-i-1}$

在立方网络中，第 $i$ v级开关最低有效位为第 $n - i - 1$ 位，并且最终映射到的目标地址中的对应位为第 $n - i - 1$ 位，所以 $t_i=d_{n-i-1}, 0 \leq i \leq n-1)$

写出 XY 多播路由算法。

【答】

目的节点集 $D^{'}$ ，本地址 $(x, y)$ ，

（1）若 $x>min\{x_i|(x_i,y_i)∈D^{'}\}$ 则把消息和列表送到节点 $(x - 1, y)$ ；若 $x<max\{x_i|(x_i,y_i)∈D^{'}\}$ 则把消息和列表送到节点 $(x + 1, y)$ 。

（2）若 $x\in \{x_i|(x_i,y_i)∈D^{'}$ ，判断 $y$ 的大小，若 $y>min\{y_i|(x_i,y_i)∈D^{'}\}$ 则把消息和列表送到 $(x, y - 1)$ ；若 $y<max\{y_i|(x_i,y_i)∈D^{'}\}$ ，则把消息和列表送到 $(x, y + 1)$ 。

（3）若 $(x,y)\in D^{'}$ ， $D^{'} \leftarrow D^{'}-(x,y)$ ，并把消息送到本地节点。

给出 6X6 网格中 双路径和多路径多播路由的路径。源节点为（4，3）,目标节点集为（0，0），（4，0），（5，1）（3，2）（0，2）（5，3）（0，3）（3，4）（1，5）（5，5）。

【答】

双路径多播路由图：

!https://s2.loli.net/2024/05/21/ex6sBVEiXd4fY8U.gif

多路径多播路由图：

在这里插入图片描述

homework3

解释采用 WB 策略的写更新和写无效协议的一致性维护过程。其中 $X$ 为更新前高速缓存中的拷贝， $X^{'}$ 为修改后的高速缓存块， $I$ 为无效的高速缓存块。

在这里插入图片描述

【答】

处理器 $P_1$ 写共享变量 $X$ 为 $X^{'}$ ，

写无效协议如图 (b) 所示，无效其他核中存在高速缓存拷贝，从而维护了一致性过程。

两种 基于总线的共享内存多处理机 分别实现了 Illinois MESI 协议和 Dragon 协议，对于给定的每个内存存取序列，比较在这两种多处理机上的执行代价，并就序列及一致性协议的特点来说明为什么有这样的性能差别。

序列 ①r1 w1 r1 w1 r2 w2 r2 w2 r3 w3 r3 w3；

序列 ②r1 r2 r3 w1 w2 w3 r1 r2 r3 w3 w1；

序列 ③r1 r2 r3 r3 w1 w1 w1 w1 w2 w3；

所有的存取操作都针对同一个内存位置，r/w 代表读/写，数字代表发出该操作的处理器。假设所有高速缓存在开始时是空的，并且使用下面的性能模型：读/写高速缓存命中，代价 1 个时钟周期；缺失引起简单的总线事务（如 BusUpgr，BusUpd），60 个时钟周期；缺失引起整个高速缓存块传输，90 时钟周期。假设所有 高速缓存是写回式，并且 MESI 协议中使用 BusUpgr 事务。

【答】

读写命中、总线事务、块传输分别简记为 $H$ 、 $B$ 、 $T$ 。

MESI 协议：

①T H H H T B H H T B H H 共 $2 B + 7 H + 3 T = 397$ 时钟周期

②T T T B T T T T H B T 共 $2 B + 1 H + 8 T = 841$ 时钟周期

③T T T H B H H H T T共 $1 B + 4 H + 5 T = 514$ 时钟周期。

Dragon协议：

①T H H H T B H B T B H B 共 $4 B + 5 H + 3 T = 515$ 时钟周期

②T T T B B B H H H B B 共 $5 B + 3 H + 3 T = 573$ 时钟周期

③T T T H B B B B B B 共 $6 B + 1 H + 3 T = 631$ 时钟周期。

由结果得出，①、③ 序列用 MESI 协议时间更少，而 ② 序列用 Dragon 协议时间更少。

综上可知，如果同一块在写操作之后频繁被多个核读操作采用 Dragon 协议更好一些，因为 Dragon 协议写操作后会更新其它核副本。如果一个同多次连续对同一块进行写操作 MESI 协议更有效，因为它不需要更新其它核副本，只需要总线事务无效其它核即可。

考虑以下代码段，说明在 顺序一致性模型 下，可能的结果是什么？假设在代码开始执行

时，所有变量初始化为0。

a.  
P1	P2	P3
A=1	U=A	V=B
	B=1	W=A

b.
P1	P2	P3	P4
A=1	U=A	B=1	W=B
	V=B		X=A

【答】

顺序一致性模型性下，保护每个进程都按程序序来发生内存操作，这样会有多种可能结果，这里假设最简单情况，即 $P_1$ 、 $P_2$ 、 $P_3$ 依次进行。则 a 中 $U = V = W = 1$ ，b 中 $U = X = W = 1$ ， $V = 0$ 。

针对以下高速缓存情况，试给出一个使得 高速缓存的包含性不满足 的内存存取序列？

$L_1$ 高速缓存容量 32 字节，2-路组相联，每个高速缓存块 8 个字节，使用 LRU 替换算法；

$L_2$ 高速缓存容量 128 字节，4-路组相联，每个高速缓存块 8 个字节，使用 LRU 替换算法。

【答】

假设 $m_1$ 、 $m_2$ 、 $m_3$ 块映射到一级 Cache 和二级 Cache 的同一组中，考虑如下内存存取序列 $R_{m_1}$ ， $R_{m_2}$ ， $R_{m_1}$ ， $R_{m_3}$ ，由 LRU 替换算法知道，当 $R_{m_3}$ 执行后， $L_1$ 中被替换出的是 $m_2$ ， $L_2$ 中被替换出的是 $m_1$ ，此时 $m_1$ 块在 $L_1$ 却不在 $L_2$ 中，不满足包含性。

利用 LL-SC 操作 实现一个 Test&Set 操作。

【答】

Test&Set：ll reg1,location /*Load-locked the location to reg1 */

          bnz reg1,lock  /* if locatin was locked,try again*/

          mov reg2,1   /*set reg2to1*/

          sc location,reg2 /*store reg2 conditional into location*/