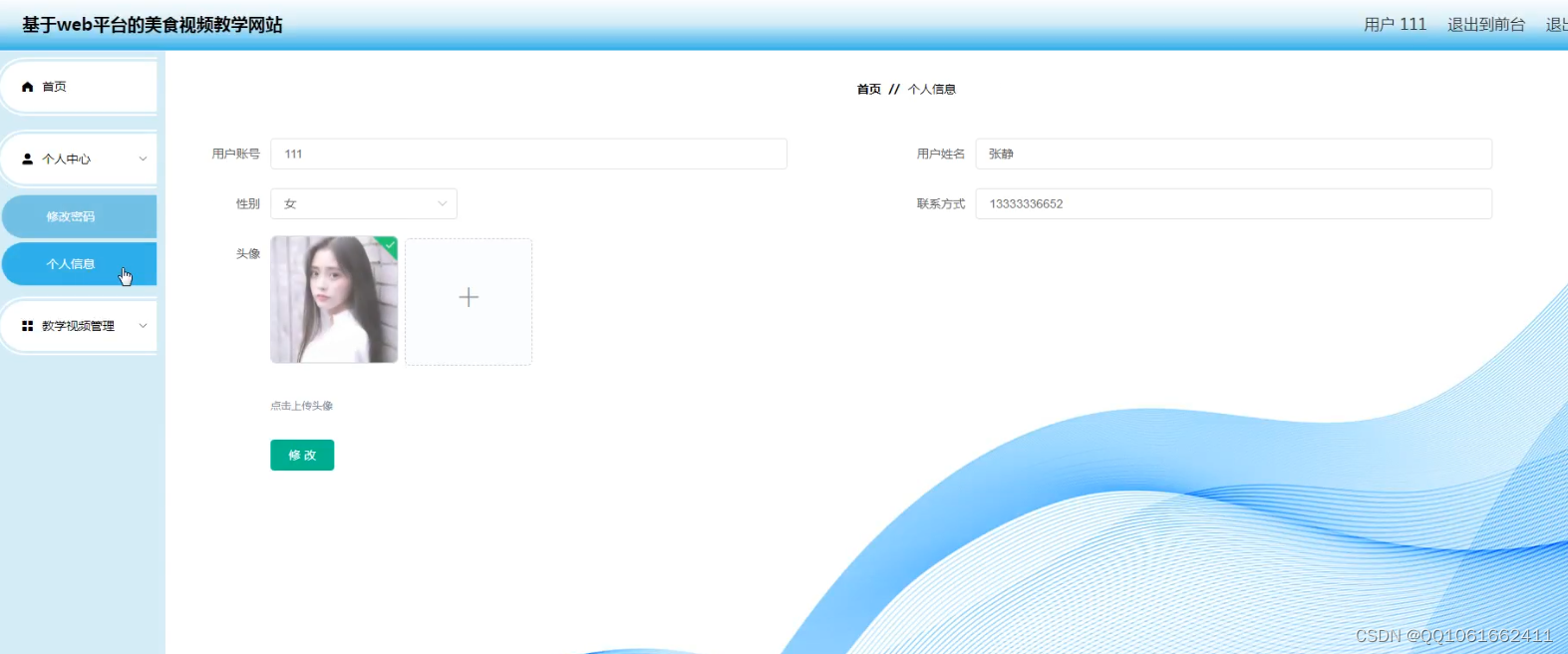
哈夫曼树：结点中赋予一个某种意义的值，称为结点的权值，从根结点开始，到目标结点经过的边数，称为路径长度，路径长度乘以权值，称为带权路径长度；

例如：根结点代表着快递集散点，一个叶子结点权值是5，在业务逻辑中代表着重量是5斤的货物📦，路径长度是3，业务逻辑代表着3公里，3 * 5 = 15 假设代表着从根结点开始配送这一件货物的成本 开销是15升汽油

越重的物品，配送距离越长，开销越大，假设说每一层结点都有一个快递柜，只可以存放一件物品，这样就让收件人自己来取，而不用大老远送过去了，那么我们就应该优先把最重的物品，放在距离快递集散点（根结点）越近的位置。重量轻的（权值小的）小件物品我们可以送远一点。
那么这个想法其实就是最短带权路径

例：假设快递站今天收到了6件需要派送的物品，重量（斤）分别是 6，9，1，3，2，12
如果快递员不懂巧妙利用最短带权路径，而是经过一个快递柜就按顺序把一件放进柜子，剩下的继续配送，那么构成的树就会是：

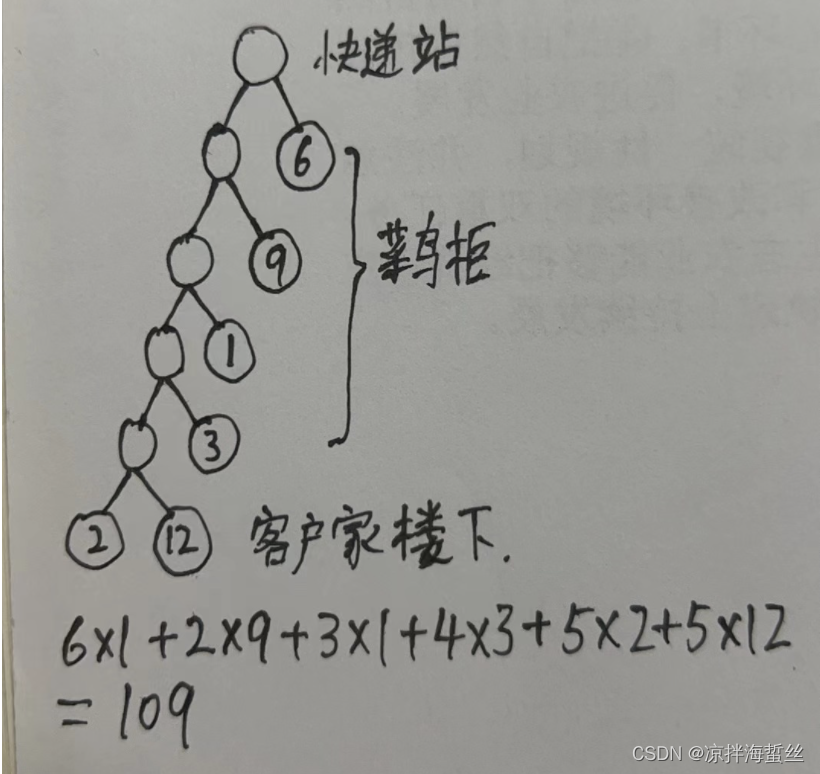
可以看到总耗费汽油109升。

但是转念一想，既然都可以放菜鸟柜，我为什么不把重的提前放下车，省点汽油呢？于是第二天快递员就改变思路，形成下面的二叉树：

果然，第二天只消耗了75升汽油，成本大大节约了

总结：综上所述，使得带权路径WPL最小的树，就称之为哈夫曼树。也可以称之为：最优二叉树

例子：

牢记哈夫曼树只有叶子结点能存放字符；同时哈夫曼树仅有度为0或者度为2的结点（因为是两两组合，不存在度为1）

（1）一棵哈夫曼树共有215个结点，对其进行哈夫曼编码，共能得到（108）个不同的码字
因为哈夫曼树只有叶子结点能存放码字
根据二叉树的性质，最后一个非叶结点是：215 / 2 向下取整 = 107
所以叶子结点就是：215 - 107 = 108
所以，能存放108个不同的码字

（2）【2019】对n个互不相同的符号进行哈夫曼编码，若生成的哈夫曼树共有115个结点，则n的值是（）
结点总数为115，则最后一个非叶结点是：115 / 2 向下取整 = 57
则叶子结点是：115 - 57 = 58
所以能存放58个不同的符号

如何生成哈夫曼树？

在上面的例子我们从根往下生成，其实步骤是不对的，只是为了举例子，更容易的找出N个结点的最小带权路径的哈夫曼树的过程应该如下：
首先把N个结点看作N棵只有一个结点的树
（1）从N个结点中找出两个最小权值的树，组成一棵新树最底端的两个叶子，同时两个结点的权值加起来生成一个新结点，该新树的权值就是原来两个树的权值之和。（这里就是哈夫曼树的萌芽）这个时候还有N-1棵树（合并两棵，生成新的一棵嘛）
（2）再从剩下的N-1棵树找到两棵权值最小的，再次组合，哈夫曼树就会产生一个新结点。剩余N-2棵树（哈夫曼树不断成长）
（3）重复 1，2步骤，直到该森林中只剩下一棵树，就是哈夫曼树。
借助上面的例子，画流程图大概就是：

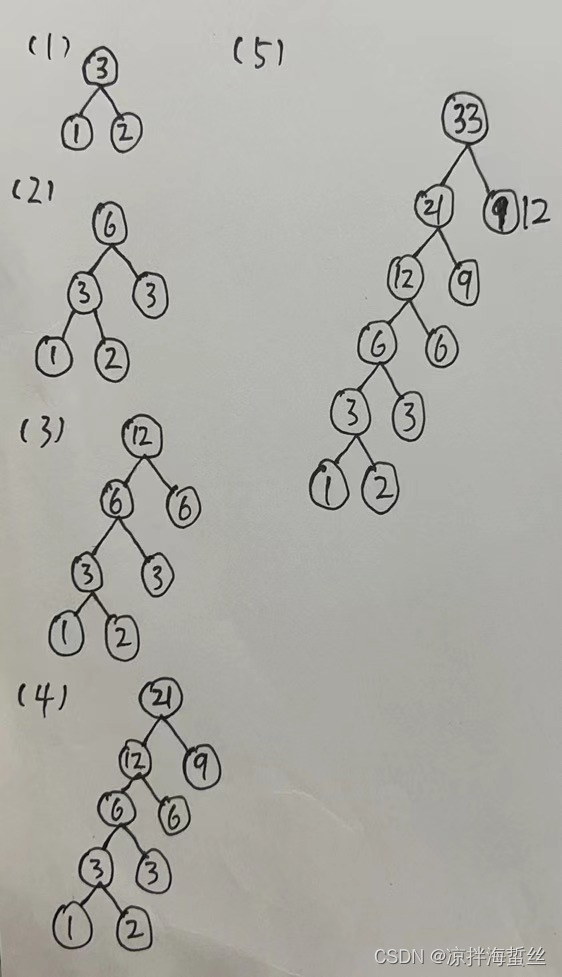
哈夫曼编码（左0右1式）

哈夫曼编码是哈夫曼树的一种使用，在上面例子中是用重量搬运的距离，但是我们也可以思考使用于加密电报和文字压缩等场景，通过变长度编码，我们可以在哈夫曼树的各个叶子结点中存放不同的文字符号

在数据通信中
若对每个字符采用相等长度的二进制位表示，称为固定长度编码；
若允许对不同字符采用不等长的二进制位表示，则称为可变长度编码。

所谓左0右1，就是从根结点开始，往左走是1，往右走是0，同时记录下走的左拐右拐，直到某个根结点，这一串01就是该根结点权值的哈夫曼编码。
在N个叶子结点中，会有N串哈夫曼编码，如果没有一串编码是另外一串编码的前缀，则称这样的编码是前缀编码，通过前缀编码可以很轻松翻译出源码。
这样会很抽象，例子：
（1）下面哪一串编码不是前缀编码？B
A {00, 01, 10, 11}
B {0, 1, 00 ,11}
C {0,10, 110, 111}
D {10, 110 ,1110, 1111}
技巧通过左0右1原则，拿着笔在草稿纸上划点，如果有一个编码的路径覆盖了某个编码，则说明不是前缀编码：

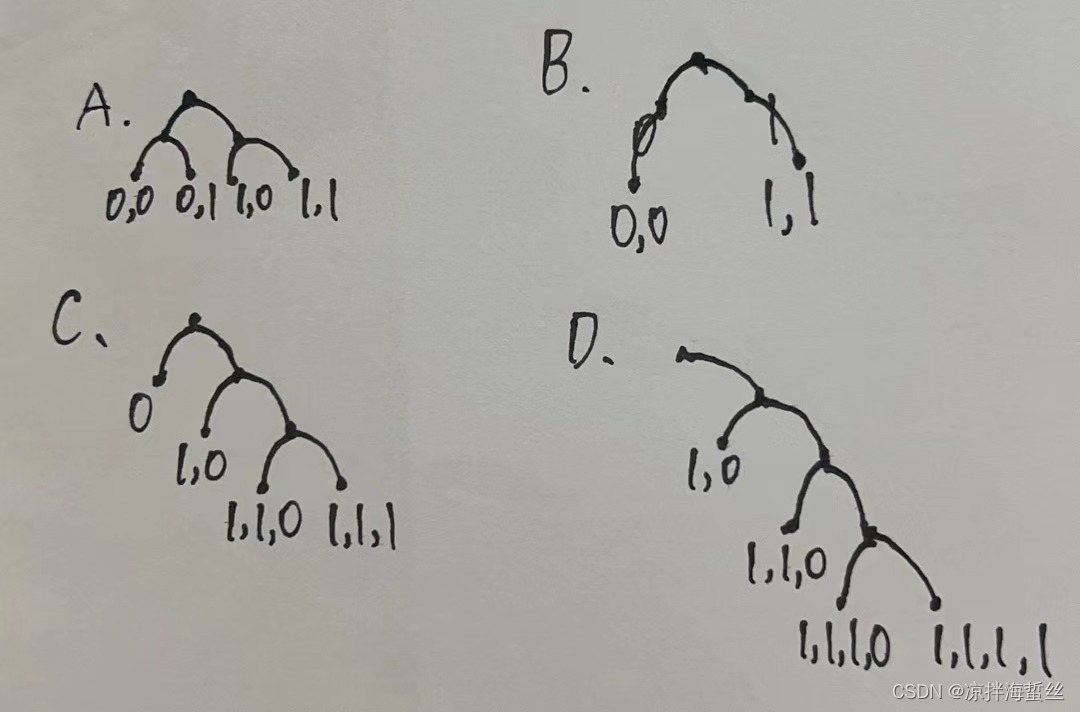
通过简单的划点，可以看到B选项中，00覆盖了0，11覆盖了1，这样当我们接到一串二进制哈夫曼编码，根本不知道00代表是 0 0 还是00

例：【2014】5个字符有如下4种编码方案，不是前缀编码的是：
01，0000，0001，001，1
011，000，001，010，1
000，001，010，011，100
0，100，110，1110，1100
还是通过上面划点，左0右1，很轻松能看到D选项的1100覆盖掉了110的路径
当然网上也有其它的办法，但是我比较笨看数字看得很晕，也怕看错，画图是我最喜欢的方式，一发生覆盖马上就知道了

简单一提，这样画图还有一个好处，就是哈夫曼编码的长度就等于其哈夫曼树的深度。知道了哈夫曼树的深度，就可以知道它能存放多少个字符/还能存放多少个字符。

【2015】下列给出的是从根分别到达两个叶子结点路径上的权值序列，属于同一棵哈夫曼树的是：
A 24，10，5 和 24，10，7
B 24，10，5 和24，12，7
C 24，10，10和24，14，11
D 24，10，5和24，14，6

要判断是否属于同一棵哈夫曼树，就要看从根结点开始，下一层的两个结点权值之和是否等于根结点的权值
A选项中根结点权值24，下一层如果有一个结点是权值10，则组成权值10的应该是5，5；但是A选项中却是5，7；这就是序列不合法
B选项中根结点权值24，下一层权值一个10，一个12，两个结点权值之和根本组不成24，所以也是序列不合法
C选项中根结点24，下一层一个权值10，一个权值14，合法； 权值为10的下一层一个权值是10，那么另外一个结点权值只能是0；权值为14的下一层的一个权值是11，另外一个结点权值只能是3。这个时候，既然这棵树最小是0，3；第一次组合不应该是0和3组合吗？为什么是0和10，3和11组合？这很明显就不是一棵哈夫曼树
D选项24权值的根分为权值10和权值14的结点，权值10的结点又分为5，5；权值14的分为6，8；组合合法。所以是D

【2017】已知字符集 {a,b,c,d,e,f,g,h} 各字符的哈夫曼编码依次是 0100，10，0000，0101，001，011，11，0001；则编码序列0100011001001011110101的译码结果是：
由于它已经是哈夫曼编码，所以一定不会有重复的前缀，大胆一个个读过去，同时根据哈夫曼编码，符合的一定就是对应的字母，不会有其它情况！大胆读过去：
0100 ： a
011: f
001: e
001: e
011: f
11:g
0101:d

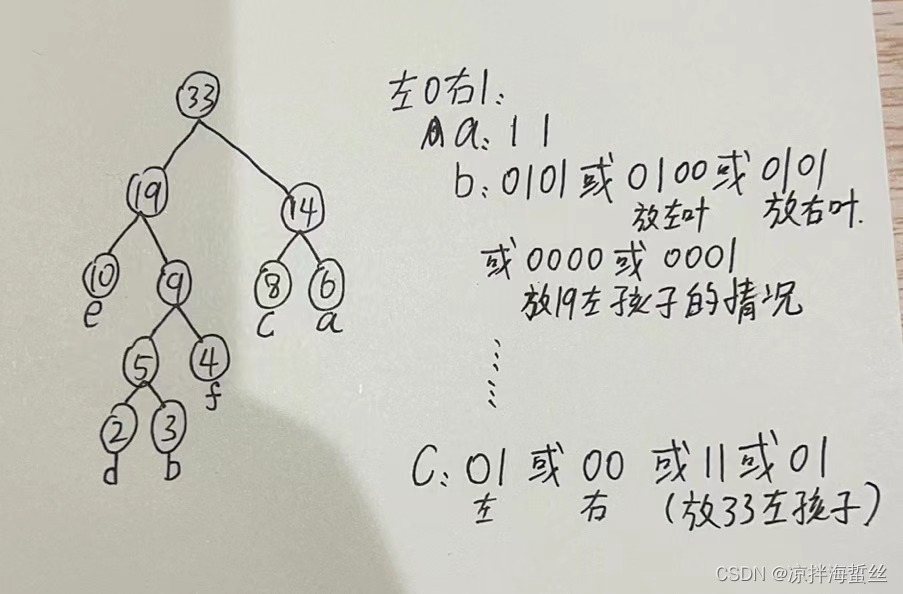
【2018】已知字符集{ a,b,c,d,e,f } ,各字符出现的次数分别是 6，3，8，2，10，4；则对应字符集中各字符的哈夫曼编码可能是：
根据哈夫曼树的原则，我们尽可能让出现次数越多的越靠前，出现次数越多，可以看作是权值越大。构建一棵二叉树，然后根据该二叉树根据左0右1的规则（也可能是左1右0的规则），生成一串哈夫曼编码。
注意由于组成对的两个结点，左右位置是任意放的，所以

【2012】设有6个有序表ABCDEF，分别含有10，35，40，50，60和200个数据元素，各表中的元素按升序排序。要求通过5次两两合并，将6个表重合并为1个升序表，并使最坏情况下比较的总次数达到最小，则：
（1）给出完整的合并过程，并求出最坏情况下比较的总次数
思路分析：
（由于题目要求的是最坏情况，那么最坏情况就是每对两两合并的升序表，它的值都是错开的不连续的，所以大小需要一一对比，例如10和200合并，就需要比较200+10 - 1 次，生成210个元素的有序新表后，再跟60比较，需要比较 210 + 60 -1 次，生成270个新元素的新表，综上，合并含有m和n个元素的有序表，比较次数是m + n -1 次）
这其实就很明显看出，如果一开始就合并大表，那么最坏情况，接下来每合并一张表，都要把大表循环比较一遍，导致比较次数最多。所以我们必须把大表放到最后比较。
所以这还是哈夫曼树的构造过程：
A和B合并，形成45个有序元素的新表（这里45看作新的树的权值），比较了44次
AB和C合并，形成了 45 + 40 = 85 个有序元素的新表（这里85看作新的树的权值），比较了84次
D和E合并，形成了50 + 60 = 110 个有序元素，比较109次
ABC和DE合并，形成了85+110 = 195 个有序元素，比较了194次
ABCDE和F合并，形成了195 + 200 = 395 个有序元素，比较了394次
所以共比较了：44 + 84 + 109 + 194 + 394 = 825次比较，这就是最少的比较次数

（2）根据你的合并过程，描述n（n>=2）个不等长升序表的合并策略，并说明理由
n个不等长升序表的合并，要按照哈夫曼树的生成原则，先进行长度最短的两个表合并形成一个新表，再在n-1个表中寻找两个长度最短的合并形成一个新表，不断进行这样的两两合并，直到只剩下1个升序表，此时就合并成功。

【2020】若任意一个字符的编码都不是其它字符编码的前缀，则称这种编码具有前缀性，现有某字符集（字符个数>=2）的不等长编码，每个字符的编码均为二进制的01序列，最长为L位，且具有前缀特性
（1）哪种数据结构适宜保存上述具有前缀特性的不等长编码？
（注意是数据结构，不能回答什么数组，链表这些存储结构！这些存储结构是数据结构的物理存储方式！）
哈夫曼树，二进制编码对应着对应字符从根结点开始往下（左0右1）的对应存放位置，二进制编码的位数表示着该叶子结点的深度，即路径长度

（2）基于设计的数据结构，简述从0/1串到字符串的译码过程
由于哈夫曼树中，对应的数据都存放在叶子结点，所以我们根据编码，从左到右依次循环，左0右1（或者左1右0），找到对应的叶子结点，就是我们需要找的字符

（3）简述判定某字符集的不等长编码是否具有前缀性的过程
不等长编码具有前缀性，最重要就是“不能覆盖别人的路径”，所以在生成的时候，把对应的不等长编码一个个读入，然后根据左0右1去寻找根结点，若有一个不等长编码覆盖了别的字符的根结点的不等长编码，则不具有前缀性。
（具体细节还可以再展开详细描述）