一、研究背景和意义
随着全球经济的不断发展和数字化转型的加速推进，科技公司在全球市场中扮演着日益重要的角色。其中，中国的阿里巴巴集团作为全球最大的电子商务公司之一，其业务范围覆盖电子商务、云计算、金融科技等多个领域。由于其在中国及全球市场的影响力和市值巨大，阿里巴巴的股票价格不仅关乎公司自身的发展状况，也反映了中国和全球经济的整体走势。股票价格是金融市场最直观、最重要的指标之一，对于投资者、分析师和政策制定者来说，了解和预测股票价格的波动具有重要的意义。时间序列分析作为一种经典的统计方法，可以帮助我们深入理解阿里巴巴股票价格的走势规律，为投资决策和风险管理提供可靠的依据。。。。
二、研究综述
在国内研究方面，翁紫霞为提供可参考的投资建议，提高投资者在股票市场的收益，基于建设银行 2019 年 1 月 2 日—2022 年11 月 14 日每个交易日共计 939 组收盘价数据，应用 ARIMA 模型对股价进行预测和分析。结果显示，应用 ARIMA 模型可对短期内股价进行很好的预测，但因股票市场受多种多重因素的影响，进行长期预测时可能存在较大误差，需要深入探索更为准确的股价预测模型[1]。。。。姚金海通过构建一个基于ARIMA与信息粒化SVR的组合预测模型，对股票市场指数价格和收益变化的趋势进行预测。实证研究结果表明：基于ARIMA与信息粒化SVR组合的股指预测模型相较于传统时间序列模型而言，在预测精度和效度方面有较大提升，能够在一定时间周期内对股票等风险资产的价格波动区间进行较为可靠地预测[7]。。。。
三、理论部分
ARIMA模型为自回归移动平均模型，这是一个当选取的序列是非平稳序列时，能够通过差分、季节分解等一系列方法后将该序列变为平稳序列，随后继续建模的一个模型
指数平滑法是一种常用于时间序列预测的简单但有效的方法之一。它的核心思想是利用过去观测值的加权平均来预测未来的值，其中过去观测值的权重随时间指数级衰减。
季节性自回归整合移动平均模型（Seasonal Autoregressive Integrated Moving Average，sARIMA）是一种用于处理具有季节性的时间序列数据的方法。它是ARIMA模型的扩展，专门设计用于捕捉数据中的季节性变化。。。。
四、实证分析
本研究使用的数据来自阿里巴巴（股票代码：SW9988）的股票市场交易数据，涵盖了从 2022 年 1 月 1 日到 2024 年 3 月 12 日的时间范围。这段时间内的交易数据记录了阿里巴巴股票在市场中的各种表现和变化。
数据和代码
报告代码数据
首先读取数据并且查看数据和其特征格式：
library(ggplot2)
library(vars)
library(readxl)
# 导入所需的库
library(readr)
# 读取CSV文件
data <- read_csv('C:/Users/DWW/Desktop/ALBB-SW9988.csv')
data
# 显示数据的前几行
head(data)
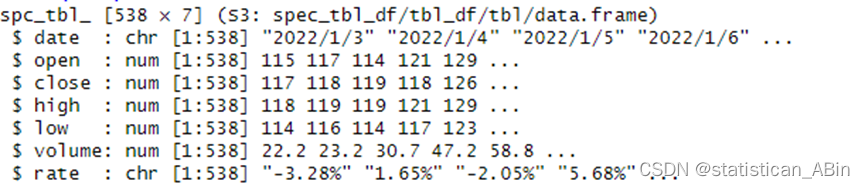从上图可以看见，其中包含了538个数据点，每个数据点有7个变量，主要是数值型和字符串形式。接下来转换日期格式并且画出时间序列图：
data$date
# 绘制时间序列图
ggplot(data, aes(x = data$date, y = ts_data)) +
geom_line() +
labs(x = "日期", y = "收盘价") +
ggtitle("收盘价时间序列") +
theme_minimal() +
theme(plot.title = element_text(hjust = 0.5))
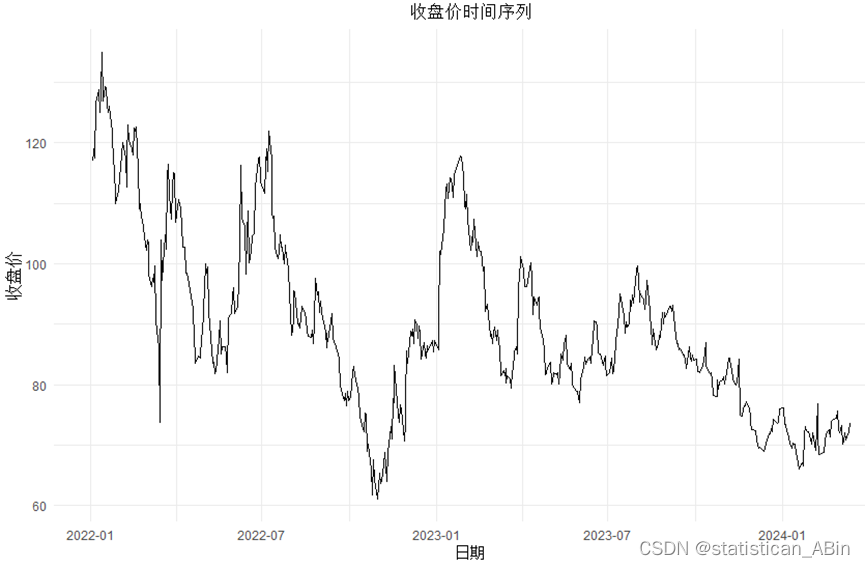
从图中可以看出几个特点，在波动性上，股票价格波动非常显著，其中在2022年中到2023年初出现较大的波峰和波谷，这意味着在这段时间内股票价格的波动幅度较大。
接下来进行平稳性检验
拒绝了原假设，这意味着我们有足够的证据来支持备择假设，即时间序列数据是平稳的。接下来画出ACF和PACF图。
# 绘制ACF图
acf(ts_data, main = "ACF Plot for ts_data")
# 绘制PACF图
pacf(ts_data, main = "PACF Plot for ts_data")
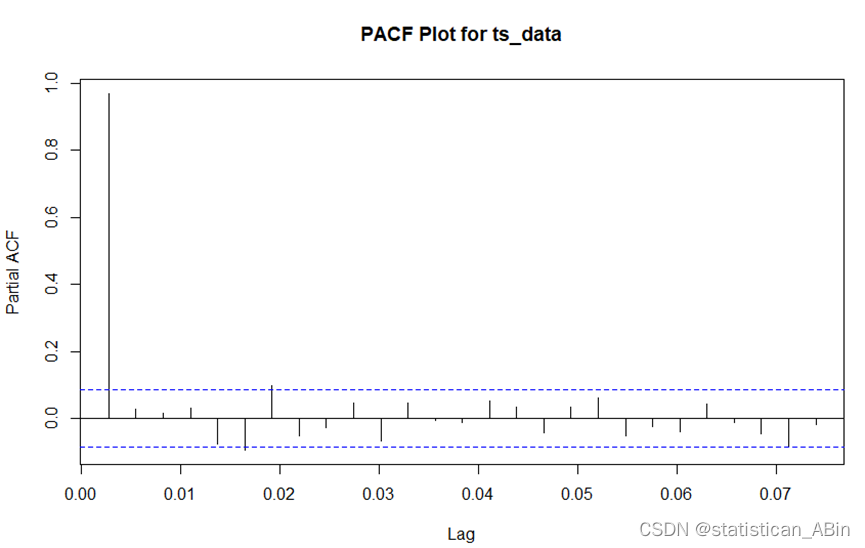ACF图显示了时间序列与其自身过去值的相关程度。这幅图显示了在多个时间滞后（Lag）下，ACF值逐渐减小。在这里，几乎所有的ACF条都是正值，并且逐渐减小到零，这通常是一个非平稳时间序列的指标。
在这里我们选取了arima (2, 0, 1)和自动定阶的模型来比较，模型信息如下：
# 拟合模型
manual_arima_model <- arima(ts_data, order = c(2, 0, 1))
# 显示手动选择的ARIMA模型信息
print(manual_arima_model)
# 模型评价
accuracy(manual_arima_model)
模型参数：ARIMA(0,1,0)表示你选择了一个差分阶数为1的一阶差分自回归移动平均模型。这个模型没有自回归项（AR）和移动平均项（MA），只有一个一阶差分（差分阶数为1）。
ARIMA(2,0,1)模型的参数为：ar1 = 1.3046, ar2 = -0.3185, ma1 = -0.3804，同时还有一个截距项(intercept)为90.3917。参数的标准误差分别为：ar1的标准误差为0.4346，ar2的标准误差为0.4245，，，
综合来看，虽然ARIMA(2,0,1)模型在参数较多的情况下拟合了数据。可以通过图来直观比较两模型的误差：
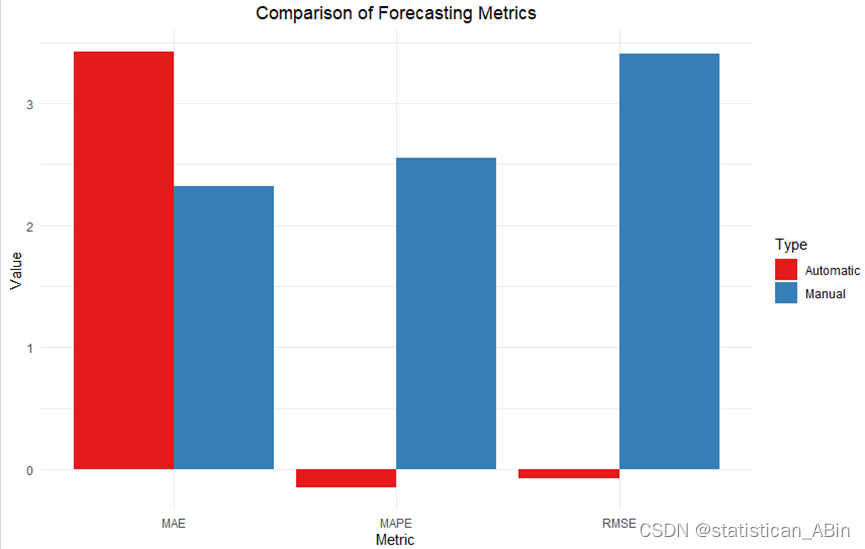
在MAE指标上，手动定阶的模型性能低于自动定阶模型，但是在RMSE和MAPE指标上，手动定阶的模型性能显著优于自动定阶模型，
接下来展示一下ARIMA(2,0,1)的预测结果：
# 绘制图表
ggplot(combined_data, aes(x=Date, y=Value, color=Data)) +
geom_line() +
labs(title="Time Series Forecast", x="Date", y="Closing Price") +
theme_minimal()+
theme(plot.title = element_text(hjust = 0.5))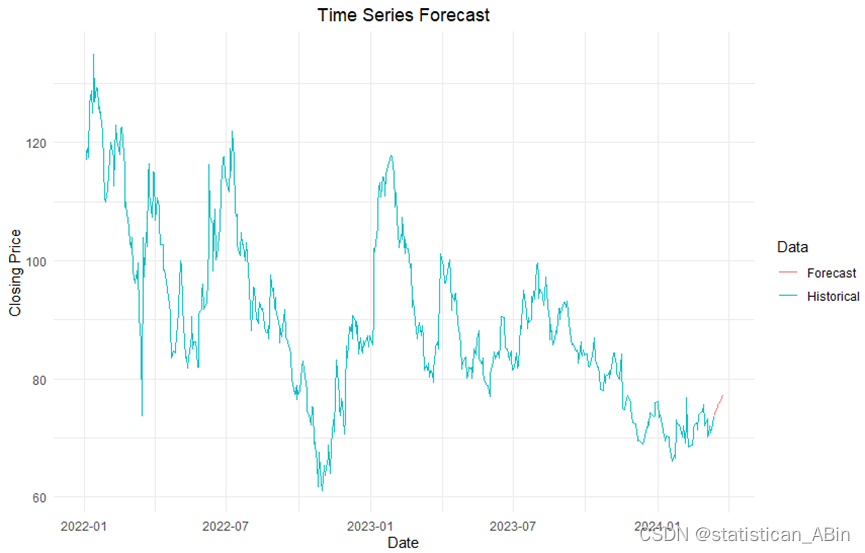
其中，蓝色线显示了2022年1月至2023年底的价格走势。可以看到价格有明显的波动，其中有几个尖峰和深谷，这表明了该期间内的高波动性。。。。
接下来对模型进行残差分析：
# 残差分析
checkresiduals(manual_arima_model)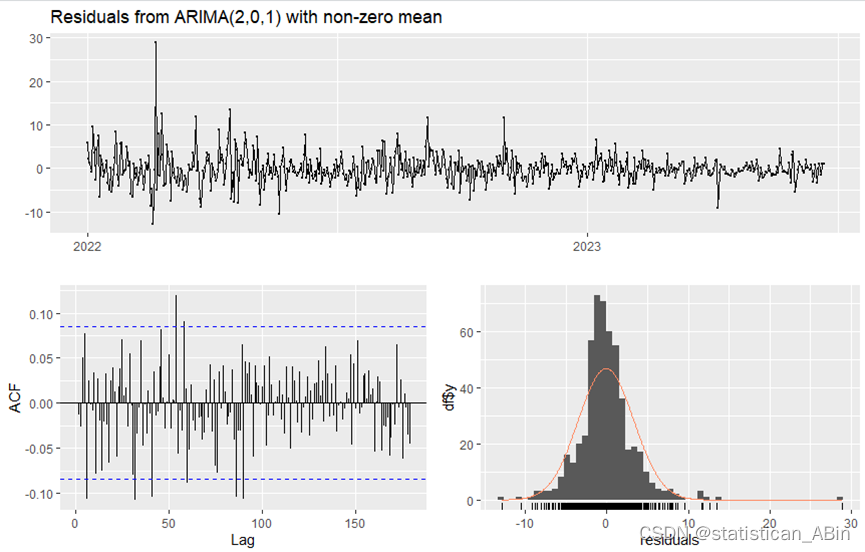
综合这些图表，我们可以得出结论，ARIMA(2,0,1)模型对数据进行了相对合理的拟合。
ETS模型
从上面结果可以得到，Smoothing parameters（平滑参数），alpha = 0.9422，这是平滑参数，它控制着对观察值的权重。较高的alpha值意味着更多的权重被分配给最近的观察值，。。
accuracy_ets <- accuracy(forecast_ets)
accuracy_ets
# 查看预测结果
plot(forecast_ets)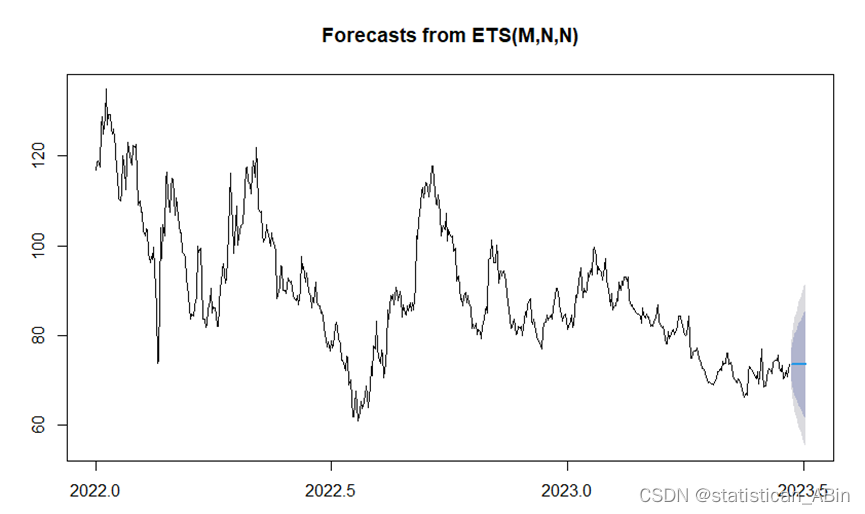
数据显示了显著的波动性和一个整体的下降趋势。从大约2023年初开始，图表以灰色区域显示了12个时间周期的预测。。。。
Prophet模型
接下来使用Prophet模型来对数据做12期的预测：
# 构建未来数据框架
future <- make_future_dataframe(m, periods=12, freq = 'day')
# 进行预测
forecast_prophet <- predict(m, future)
forecast_prophet
# 查看预测结果
plot(m, forecast_prophet)
prophet_plot_components(m, forecast_prophet)
Prophet是Facebook开发的一个开源工具，它适用于时间序列数据的预测，特别是对于具有强季节性模式和多个季节性周期的数据。 特别的，该模型的指标情况为：MAE为5.2771，RMSE:为6.7873，MAPE: 0.0612。
SARIMA模型以及混合模型ARIMA-ETS
首先看一下SARIMA模型
fit_sarima <- auto.arima(data_ts, seasonal=TRUE)
# 概览模型
summary(fit_sarima)
# 进行预测
forecast_sarima <- forecast(fit_sarima, h=12)
# 查看预测结果
plot(forecast_prophet)
从上述模型参数可以知道，每个参数的标准误差（s.e.）分别为：ar1的标准误差为0.0686，ar2的标准误差为0.0658，。。
接下来进行混合模型的预测实验：
# 可视化预测结果
plot(forecast_arima, col="blue")
lines(forecast_ets$mean, col="red")
lines(combined_forecast, col="green")
legend("topright", legend=c("ARIMA", "ETS", "Combined"), col=c("blue", "red", "green"), lty=1)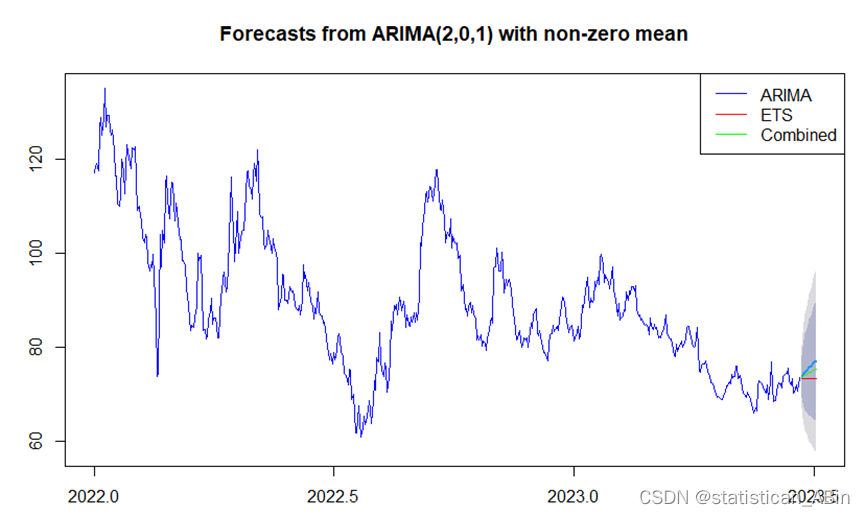
从上图可以看出，ETS的预测是一条直线，说明预测未来股价会一直平稳，但是这可能性很小，从混合模型ARIMA-ETS和ARIMA模型对比来看，并不是模型通过混合之后其预测效果会变得更好，反之，有可能不如单一的时间序列模型。
五、结论和政策建议
在建模方面，我们尝试了多种时间序列模型，包括ARIMA、ETS、Prophet和SARIMA等。经过比较，我们发现ARIMA(2,0,1)模型在拟合数据和预测效果上表现较好，具有较低的预测误差和较高的拟合优度指标。。。。
参考文献
- 翁紫霞.基于ARIMA模型的股价分析与预测——以建设银行为例[J].现代信息科技,2023,7(14):137-141.DOI:10.19850/j.cnki.2096-4706.2023.14.029.
- 万文娣. 机器学习在股票价格混合预测模型中的研究与应用[D].西北师范大学,2023.DOI:10.27410/d.cnki.gxbfu.2023.002345.
- 刘祺,施三支,娄磊等.基于ARIAM-GARCH深度学习的股价预测与决策[J].长春理工大学学报(自然科学版),2024,47(01):119-130.、
创作不易，希望大家多点赞关注评论！！！（类似代码或报告定制可以私信）
