- 第二次作业
- 计算题
- 编程题
第二次作业
计算题
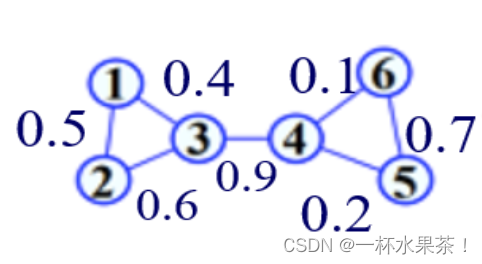
给定图 G G G(如图 1,图中数值为边权值),图切割将其分割成多个互不连通的⼦图。请使⽤谱聚类算法将图 G G G 聚类成 k = 2 k = 2 k=2 类,使得:
(a) RatioCut 最⼩;
(b) NormalizedCut 最⼩。
并给出计算过程,以及对应的 RatioCut 值和 NormalizedCut 值。
【解】
该图的邻接矩阵表示为:
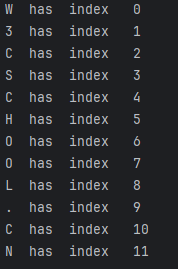
W
=
[
0
0.5
0.4
0
0
0
0.5
0
0.6
0
0
0
0.4
0.6
0
0.9
0
0
0
0
0.9
0
0.2
0.1
0
0
0
0.2
0
0.7
0
0
0
0.1
0.7
0
]
W = \begin{bmatrix} 0 & 0.5 & 0.4 & 0 & 0 & 0 \\ 0.5 & 0 & 0.6 & 0 & 0 & 0 \\ 0.4 & 0.6 & 0 & 0.9 & 0 & 0 \\ 0 & 0 & 0.9 & 0 & 0.2 & 0.1 \\ 0 & 0 & 0 & 0.2 & 0 & 0.7 \\ 0 & 0 & 0 & 0.1 & 0.7 & 0 \end{bmatrix}
W=
00.50.40000.500.60000.40.600.900000.900.20.10000.200.70000.10.70
度矩阵为:
D
=
[
0.9
0
0
0
0
0
0
1.1
0
0
0
0
0
0
1.9
0
0
0
0
0
0
1.2
0
0
0
0
0
0
0.9
0
0
0
0
0
0
0.8
]
D = \begin{bmatrix} 0.9 & 0 & 0 & 0 & 0 & 0 \\ 0 & 1.1 & 0 & 0 & 0 & 0 \\ 0 & 0 & 1.9 & 0 & 0 & 0 \\ 0 & 0 & 0 & 1.2 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0.9 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0.8 \end{bmatrix}
D=
0.90000001.10000001.90000001.20000000.90000000.8
(a)RatioCut 最⼩
拉普拉斯矩阵为:
L
=
D
−
W
=
[
0.9
−
0.5
−
0.4
0
0
0
−
0.5
1.1
−
0.6
0
0
0
−
0.4
−
0.6
1.9
−
0.9
0
0
0
0
−
0.9
1.2
−
0.2
−
0.1
0
0
0
−
0.2
0.9
−
0.7
0
0
0
−
0.1
−
0.7
0.8
]
L = D - W = \begin{bmatrix} 0.9 & -0.5 & -0.4 & 0 & 0 & 0 \\ -0.5 & 1.1 & -0.6 & 0 & 0 & 0 \\ -0.4 & -0.6 & 1.9 & -0.9 & 0 & 0 \\ 0 & 0 & -0.9 & 1.2 & -0.2 & -0.1 \\ 0 & 0 & 0 & -0.2 & 0.9 & -0.7 \\ 0 & 0 & 0 & -0.1 & -0.7 & 0.8 \end{bmatrix}
L=D−W=
0.9−0.5−0.4000−0.51.1−0.6000−0.4−0.61.9−0.90000−0.91.2−0.2−0.1000−0.20.9−0.7000−0.1−0.70.8
其特征值为:
λ
=
[
0
0.16611
0.87866
1.49543
1.55934
2.70047
]
\lambda =\begin{bmatrix} 0 \\ 0.16611 \\ 0.87866 \\ 1.49543 \\ 1.55934 \\ 2.70047\end{bmatrix}
λ=
00.166110.878661.495431.559342.70047
对应的特征向量为:
X
=
[
0.40825
0.40239
0.48507
0.64252
0.11036
−
0.10542
0.40825
0.38254
0.26567
−
0.71241
−
0.18567
−
0.27279
0.40825
0.2601
−
0.30622
−
0.06593
0.05017
0.81551
0.40825
0.06722
−
0.7402
0.15974
0.09372
−
0.4966
0.40825
−
0.53361
0.0817
0.14535
−
0.71975
0.05253
0.40825
−
0.57865
0.21398
−
0.16927
0.65116
0.00678
]
X= \begin{bmatrix} 0.40825 & 0.40239 & 0.48507 & 0.64252 & 0.11036 & -0.10542 \\ 0.40825 & 0.38254 & 0.26567 & -0.71241 & -0.18567 & -0.27279 \\ 0.40825 & 0.2601 & -0.30622 & -0.06593 & 0.05017 & 0.81551 \\ 0.40825 & 0.06722 & -0.7402 & 0.15974 & 0.09372 & -0.4966 \\ 0.40825 & -0.53361 & 0.0817 & 0.14535 & -0.71975 & 0.05253 \\ 0.40825 & -0.57865 & 0.21398 & -0.16927 & 0.65116 & 0.00678 \end{bmatrix}
X=
0.408250.408250.408250.408250.408250.408250.402390.382540.26010.06722−0.53361−0.578650.485070.26567−0.30622−0.74020.08170.213980.64252−0.71241−0.065930.159740.14535−0.169270.11036−0.185670.050170.09372−0.719750.65116−0.10542−0.272790.81551−0.49660.052530.00678
对应
λ
2
\lambda_2
λ2 的特征向量
x
2
x_2
x2 进行聚类,显然 1、2、3、4 为一类,5、6 为一类。
则
R
a
t
i
o
C
u
t
=
1
2
(
0.3
4
+
0.3
2
)
=
9
80
RatioCut =\frac{1}{2}(\frac{0.3}{4}+\frac{0.3}{2}) = \frac{9}{80}
RatioCut=21(40.3+20.3)=809
(b)NormalizedCut 最小
归一化的 Laplacian 矩阵
D
−
1
/
2
L
D
−
1
/
2
D^{-1/2}LD^{-1/2}
D−1/2LD−1/2 为:
[
1
−
0.50251891
−
0.30588765
0
0
0
−
0.50251891
1
−
0.41502868
0
0
0
−
0.30588765
−
0.41502868
1
−
0.59603956
0
0
0
0
−
0.59603956
1
−
0.19245009
−
0.10206207
0
0
0
−
0.19245009
1
−
0.82495791
0
0
0
−
0.10206207
−
0.82495791
1
]
\begin{bmatrix} 1 &-0.50251891 &-0.30588765 & 0 & 0 & 0 \\ -0.50251891 & 1 &-0.41502868 & 0 & 0 & 0 \\ -0.30588765 &-0.41502868 & 1 &-0.59603956 & 0 & 0 \\ 0 & 0 &-0.59603956 & 1 &-0.19245009 &-0.10206207\\ 0 & 0 & 0 &-0.19245009 & 1 &-0.82495791\\ 0 & 0 & 0 &-0.10206207 &-0.82495791 & 1 \\ \end{bmatrix}
1−0.50251891−0.30588765000−0.502518911−0.41502868000−0.30588765−0.415028681−0.596039560000−0.596039561−0.19245009−0.10206207000−0.192450091−0.82495791000−0.10206207−0.824957911
特征值:
λ
=
[
0
0.16610702
0.87866007
1.49542669
1.55933786
2.70046837
]
\lambda = \begin{bmatrix} 0 \\ 0.16610702 \\ 0.87866007 \\ 1.49542669 \\ 1.55933786 \\ 2.70046837 \end{bmatrix}
λ=
00.166107020.878660071.495426691.559337862.70046837
特征向量:
X
=
[
0.36380344
0.32111434
0.46859317
−
0.73715774
−
0.03109895
0.02417422
0.40219983
0.34555671
0.41895846
0.63385743
−
0.36350558
0.09689228
0.52859414
0.29700834
−
0.33377341
0.14238799
0.67065213
−
0.22565677
0.42008403
0.00503849
−
0.66179385
−
0.18039115
−
0.54411556
0.23860055
0.36380344
−
0.58690394
0.13587453
−
0.00424251
−
0.18874965
−
0.68489744
0.34299717
−
0.58718018
0.19250083
0.04460851
0.29229112
0.64272217
]
X= \begin{bmatrix} 0.36380344 & 0.32111434 & 0.46859317 &-0.73715774 &-0.03109895 & 0.02417422\\ 0.40219983 & 0.34555671 & 0.41895846 & 0.63385743 &-0.36350558 & 0.09689228\\ 0.52859414 & 0.29700834 &-0.33377341 & 0.14238799 & 0.67065213 &-0.22565677\\ 0.42008403 & 0.00503849 &-0.66179385 &-0.18039115 &-0.54411556 & 0.23860055\\ 0.36380344 &-0.58690394 & 0.13587453 &-0.00424251 &-0.18874965 &-0.68489744\\ 0.34299717 &-0.58718018 & 0.19250083 & 0.04460851 & 0.29229112 & 0.64272217\\ \end{bmatrix}
X=
0.363803440.402199830.528594140.420084030.363803440.342997170.321114340.345556710.297008340.00503849−0.58690394−0.587180180.468593170.41895846−0.33377341−0.661793850.135874530.19250083−0.737157740.633857430.14238799−0.18039115−0.004242510.04460851−0.03109895−0.363505580.67065213−0.54411556−0.188749650.292291120.024174220.09689228−0.225656770.23860055−0.684897440.64272217
对
λ
2
\lambda_2
λ2 对应的特征向量进行聚类,易知 1、2、3、4 为一类,5、6 为一类。
N
o
r
m
a
l
i
z
e
d
C
u
t
=
1
2
(
0.3
5.1
+
0.3
1.7
)
=
2
17
NormalizedCut = \frac{1}{2} (\frac{0.3}{5.1} + \frac{0.3}{1.7} )=\frac{2}{17}
NormalizedCut=21(5.10.3+1.70.3)=172
- 参数未知的正态分布⽣成了如下 4 个数据:-12.2119174, 7.62328757, 9.60884573, -8.36968016。请使⽤极⼤似然估计⽅法估计出正态分布的参数,写出计算过程。(注:若数值计算过程较为复杂,可以使⽤ python 相关库进⾏计算,但仍需给出计算推导过程。)
【解】
设总体服从正态分布:
f
(
x
)
=
1
2
π
σ
e
−
(
x
−
μ
)
2
2
σ
2
f(x)=\frac1{\sqrt{2\pi}\sigma}e^{-\frac{(x-\mu)^2}{2\sigma^2}}
f(x)=2πσ1e−2σ2(x−μ)2
有一组观测值为
X
1
,
X
2
,
.
.
.
,
X
n
X_1,X_2,...,X_n
X1,X2,...,Xn,似然函数以及对数函数为:
L
(
μ
,
σ
2
)
=
∏
i
=
1
n
1
2
π
σ
e
−
(
X
i
−
μ
)
2
2
σ
2
ln
L
(
μ
,
σ
2
)
=
−
n
2
ln
(
2
π
)
−
n
ln
(
σ
)
−
1
2
σ
2
∑
i
=
1
n
(
X
i
−
μ
)
2
\begin{aligned} L(\mu,\sigma^{2}) &=\prod_{i=1}^{n}\frac{1}{\sqrt{2\pi}\sigma}e^{-\frac{(X_{i}-\mu)^{2}}{2\sigma^{2}}} \\ \ln L(\mu,\sigma^2)&=-\frac{n}{2}\ln(2\pi)-n\ln(\sigma)-\frac{1}{2\sigma^2}\sum_{i=1}^{n}(X_i-\mu)^2 \end{aligned}
L(μ,σ2)lnL(μ,σ2)=i=1∏n2πσ1e−2σ2(Xi−μ)2=−2nln(2π)−nln(σ)−2σ21i=1∑n(Xi−μ)2
分别对两个参数求导数:
∂
ln
L
(
μ
,
σ
2
)
∂
μ
=
∑
i
=
1
n
(
X
i
−
μ
)
σ
2
=
0
∂
ln
L
(
μ
,
σ
2
)
∂
σ
2
=
−
n
2
σ
2
+
∑
i
=
1
n
(
X
i
−
μ
)
2
2
σ
4
=
0
\frac{\partial\ln L(\mu,\sigma^2)}{\partial\mu} =\frac{\sum_{i=1}^n(X_i-\mu)}{\sigma^2}=0 \\ \frac{\partial\ln L(\mu,\sigma^2)}{\partial\sigma^2} =-\frac n{2\sigma^2}+\frac{\sum_{i=1}^n(X_i-\mu)^2}{2\sigma^4}=0 \\
∂μ∂lnL(μ,σ2)=σ2∑i=1n(Xi−μ)=0∂σ2∂lnL(μ,σ2)=−2σ2n+2σ4∑i=1n(Xi−μ)2=0
解得:
μ
^
=
X
‾
σ
^
2
=
n
−
1
n
S
2
\hat{\mu}=\overline{X} \\ \hat{\sigma}^2=\frac{n-1}nS^2
μ^=Xσ^2=nn−1S2
经计算:
μ ^ = − 0.8373660650000001 σ ^ 2 = 91.70554362393045 \hat{\mu} = -0.8373660650000001\\ \hat{\sigma}^2 = 91.70554362393045 μ^=−0.8373660650000001σ^2=91.70554362393045
HITS 全称是 Hyperlink-Induced Topic Search,即超链接诱导主题搜索,是⼀个链接分析⽅法,由康奈尔⼤学的 Kleinberg 教授提出。HITS 算法中有 2 个⽐较重要的概念,⼀个是“Authority”⻚⾯,另⼀个是“Hub”⻚⾯。“Authority”,即权威,所有权威⻚⾯,是指⻚⾯本⾝的质量⽐较⾼,⽐如,百度搜索或者⾕歌搜索⾸⻚。“Hub”,即枢纽,表示本⻚⾯指向的其他很多⾼质量的“Authority”⻚⾯。⼀个好的“Authority”会被很多好的“Hub”⻚⾯指向。⼀个好的“Hub”⻚⾯会指向很多好的“Authority”⻚⾯。权威值和枢纽值是互相依存、互相影响的。⽹⻚的权威值是所有指向它的⽹⻚的枢纽值之和:
a u t h ( p ) = ∑ q ∈ { 指向 p 的网页 } h u b ( q ) auth(p)=\sum_{q\in\{指向p的网页\}}hub(q) auth(p)=q∈{指向p的网页}∑hub(q)
⽹⻚的枢纽值是所有它指向⽹⻚的权威值之和:
h u b ( p ) = ∑ q ∈ { p 指向的网页 } a u t h ( q ) hub(p)=\sum_{q\in\{p指向的网页\}}auth(q) hub(p)=q∈{p指向的网页}∑auth(q)
HITS 算法流程如下:
初始化:将各节点的权威值和枢纽值均设为 1。
更新节点的权威值;
更新节点的枢纽值;
将权威值和枢纽值归⼀化,即权威值和枢纽值分别和为 1;
重复 2-4 步骤,直⾄最终收敛。
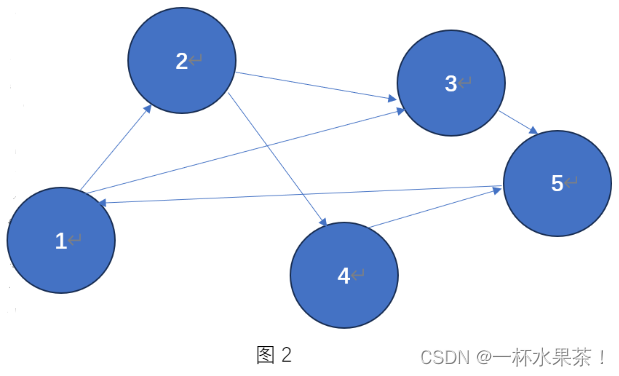
(a)根据如图 2 所示的⽹络关系,每个节点的 PageRank 初始值都是 1 写出 PageRank 算法前两轮迭代的过程。
(b)根据如图 2 所示的⽹络关系,每个节点的初始权威值和枢纽值均设为 1,写出 HITS 算法前两轮迭代的过程。
【解】
(a)PageRank
PageRank 转移矩阵为:
M
=
[
0
0
0
0
1
1
/
2
0
0
0
0
1
/
2
1
/
2
0
0
0
0
1
/
2
0
0
0
0
0
1
1
0
]
M = \begin{bmatrix} 0 & 0 & 0 & 0 & 1 \\ 1/2 & 0 & 0 & 0 & 0 \\ 1/2 & 1/2 & 0 & 0 & 0 \\ 0 & 1/2 & 0 & 0 & 0 \\ 0 & 0 & 1 & 1 & 0 \end{bmatrix}
M=
01/21/200001/21/20000010000110000
每个节点的 PageRank 初始值都是 1 ,即
P
R
0
(
n
1
)
=
1
,
P
R
0
(
n
2
)
=
1
,
P
R
0
(
n
3
)
=
1
,
P
R
0
(
n
4
)
=
1
,
P
R
0
(
n
5
)
=
1
PR^0(n_1)=1, PR^0(n_2) = 1,PR^0(n_3)=1,PR^0(n_4) = 1,PR^0(n_5)=1
PR0(n1)=1,PR0(n2)=1,PR0(n3)=1,PR0(n4)=1,PR0(n5)=1
[ n 1 n 2 n 3 n 4 n 5 ] = [ 1 1 1 1 1 ] \begin{bmatrix} n_1 \\ n_2\\ n_3\\ n_4 \\ n_5 \end{bmatrix} = \begin{bmatrix} 1 \\ 1\\ 1\\ 1 \\ 1 \end{bmatrix} n1n2n3n4n5 = 11111
第一次迭代:
[
0
0
0
0
1
1
/
2
0
0
0
0
1
/
2
1
/
2
0
0
0
0
1
/
2
0
0
0
0
0
1
1
0
]
[
1
1
1
1
1
]
=
[
1
1
/
2
1
1
/
2
2
]
\begin{bmatrix} 0 & 0 & 0 & 0 & 1 \\ 1/2 & 0 & 0 & 0 & 0 \\ 1/2 & 1/2 & 0 & 0 & 0 \\ 0 & 1/2 & 0 & 0 & 0 \\ 0 & 0 & 1 & 1 & 0 \end{bmatrix} \begin{bmatrix} 1 \\ 1\\ 1\\ 1 \\ 1 \end{bmatrix} = \begin{bmatrix} 1 \\ 1/2\\ 1\\ 1/2 \\ 2 \end{bmatrix}
01/21/200001/21/20000010000110000
11111
=
11/211/22
即
P
R
1
(
n
1
)
=
1
,
P
R
1
(
n
2
)
=
1
/
2
,
P
R
1
(
n
3
)
=
1
,
P
R
1
(
n
4
)
=
1
/
2
,
P
R
1
(
n
5
)
=
2
PR^1(n_1)=1, PR^1(n_2) = 1/2,PR^1(n_3)=1,PR^1(n_4) = 1/2,PR^1(n_5)=2
PR1(n1)=1,PR1(n2)=1/2,PR1(n3)=1,PR1(n4)=1/2,PR1(n5)=2;
第二次迭代:
[
0
0
0
0
1
1
/
2
0
0
0
0
1
/
2
1
/
2
0
0
0
0
1
/
2
0
0
0
0
0
1
1
0
]
[
1
1
/
2
1
1
/
2
2
]
=
[
2
1
/
2
3
/
4
1
/
4
3
/
2
]
\begin{bmatrix} 0 & 0 & 0 & 0 & 1 \\ 1/2 & 0 & 0 & 0 & 0 \\ 1/2 & 1/2 & 0 & 0 & 0 \\ 0 & 1/2 & 0 & 0 & 0 \\ 0 & 0 & 1 & 1 & 0 \end{bmatrix}\begin{bmatrix} 1 \\ 1/2\\ 1\\ 1/2 \\ 2 \end{bmatrix} = \begin{bmatrix} 2 \\ 1/2\\ 3/4\\ 1/4 \\ 3/2 \end{bmatrix}
01/21/200001/21/20000010000110000
11/211/22
=
21/23/41/43/2
即
P
R
2
(
n
1
)
=
2
,
P
R
2
(
n
2
)
=
1
/
2
,
P
R
2
(
n
3
)
=
3
/
4
,
P
R
2
(
n
4
)
=
1
/
4
,
P
R
2
(
n
5
)
=
3
/
2
PR^2(n_1)=2, PR^2(n_2) = 1/2,PR^2(n_3)=3/4,PR^2(n_4) = 1/4,PR^2(n_5)=3/2
PR2(n1)=2,PR2(n2)=1/2,PR2(n3)=3/4,PR2(n4)=1/4,PR2(n5)=3/2。
(b)HITS
网页的初始权威值和枢纽值如下:
A
U
T
H
0
=
[
1
1
1
1
1
]
,
H
U
B
0
=
[
1
1
1
1
1
]
AUTH^0 = \begin{bmatrix}1\\1\\1\\1\\ 1 \end{bmatrix}, HUB^0= \begin{bmatrix}1\\1\\1\\1\\ 1 \end{bmatrix}
AUTH0=
11111
,HUB0=
11111
更新权威值规则如下:
a
u
t
h
t
+
1
(
n
1
)
=
h
u
b
t
(
n
5
)
a
u
t
h
t
+
1
(
n
2
)
=
h
u
b
t
(
n
1
)
a
u
t
h
t
+
1
(
n
3
)
=
h
u
b
t
(
n
1
)
+
h
u
b
t
(
n
2
)
a
u
t
h
t
+
1
(
n
4
)
=
h
u
b
t
(
n
2
)
a
u
t
h
t
+
1
(
n
5
)
=
h
u
b
t
(
n
3
)
+
h
u
b
t
(
n
4
)
\begin{aligned} auth^{t+1}(n_1)&=hub^t(n_5) \\ auth^{t+1}(n_2)&=hub^t(n_1) \\ auth^{t+1}(n_3)&=hub^t(n_1)+hub^t(n_2) \\ auth^{t+1}(n_4)&=hub^t(n_2) \\ auth^{t+1}(n_5)&=hub^t(n_3)+hub^t(n_4) \\ \end{aligned}
autht+1(n1)autht+1(n2)autht+1(n3)autht+1(n4)autht+1(n5)=hubt(n5)=hubt(n1)=hubt(n1)+hubt(n2)=hubt(n2)=hubt(n3)+hubt(n4)
更新枢纽值规则如下:
h
u
b
t
(
n
1
)
=
a
u
t
h
t
(
n
2
)
+
a
u
t
h
t
(
n
3
)
h
u
b
t
(
n
2
)
=
a
u
t
h
t
(
n
3
)
+
a
u
t
h
t
(
n
4
)
h
u
b
t
(
n
3
)
=
a
u
t
h
t
(
n
5
)
h
u
b
t
(
n
4
)
=
a
u
t
h
t
(
n
5
)
h
u
b
t
(
n
5
)
=
a
u
t
h
t
(
n
1
)
\begin{aligned} hub^{t}(n_1)&=auth^t(n_2) + auth^t(n_3) \\ hub^{t}(n_2)&=auth^t(n_3) + auth^t(n_4) \\ hub^{t}(n_3)&=auth^t(n_5)\\ hub^{t}(n_4)&=auth^t(n_5) \\ hub^{t}(n_5)&=auth^t(n_1)\\ \end{aligned}
hubt(n1)hubt(n2)hubt(n3)hubt(n4)hubt(n5)=autht(n2)+autht(n3)=autht(n3)+autht(n4)=autht(n5)=autht(n5)=autht(n1)
第一次迭代:
A
U
T
H
1
=
[
1
1
2
1
2
]
,
H
U
B
1
=
[
3
3
2
2
1
]
AUTH^1 = \begin{bmatrix}1\\1\\2\\1\\ 2 \end{bmatrix}, HUB^1= \begin{bmatrix}3\\3\\2\\2\\1 \end{bmatrix}
AUTH1=
11212
,HUB1=
33221
进行归一化,
A
U
T
H
1
=
[
1
7
1
7
2
7
1
7
2
7
]
,
H
U
B
1
=
[
3
11
3
11
2
11
2
11
1
11
]
AUTH^1 = \begin{bmatrix} \frac{1}{7}\\ \frac{1}{7}\\ \frac{2}{7}\\ \frac{1}{7}\\ \frac{2}{7} \end{bmatrix}, HUB^1= \begin{bmatrix}\frac{3}{11}\\ \frac{3}{11}\\ \frac{2}{11}\\ \frac{2}{11}\\ \frac{1}{11} \end{bmatrix}
AUTH1=
7171727172
,HUB1=
113113112112111
第二次迭代:
A
U
T
H
2
=
[
1
11
3
11
6
11
3
11
4
11
]
,
H
U
B
2
=
[
9
11
9
11
4
11
4
11
1
11
]
AUTH^2 = \begin{bmatrix}\frac{1}{11}\\ \frac{3}{11}\\ \frac{6}{11}\\ \frac{3}{11}\\ \frac{4}{11}\end{bmatrix}, HUB^2= \begin{bmatrix}\frac{9}{11}\\ \frac{9}{11}\\ \frac{4}{11}\\ \frac{4}{11}\\ \frac{1}{11} \end{bmatrix}
AUTH2=
111113116113114
,HUB2=
119119114114111
进行归一化,
A
U
T
H
2
=
[
1
17
3
17
6
17
3
17
4
17
]
,
H
U
B
2
=
[
1
3
1
3
4
27
4
27
1
27
]
AUTH^2 = \begin{bmatrix}\frac{1}{17}\\ \frac{3}{17}\\ \frac{6}{17}\\ \frac{3}{17}\\ \frac{4}{17}\end{bmatrix}, HUB^2= \begin{bmatrix}\frac{1}{3}\\ \frac{1}{3}\\ \frac{4}{27}\\ \frac{4}{27}\\ \frac{1}{27} \end{bmatrix}
AUTH2=
171173176173174
,HUB2=
3131274274271
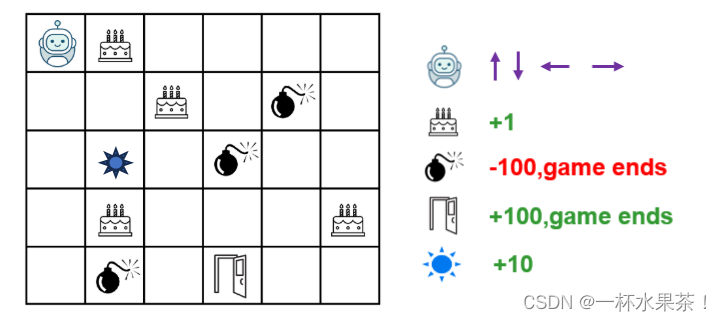
- 假设机器⼈必须越过迷宫并到达终点。有地雷,机器⼈⼀次只能移动⼀个地砖。 如果机器⼈踏上地雷,机器⼈就死了。机器⼈必须在尽可能短的时间内到达终点。请给出第 1 轮之后和第 2 轮之后 Q-table 中每个位置的值。并对第⼀列的所有值写出计算过程。学习率设为 0.2,折扣因⼦为 0.1。
【解】
Q Q Q 函数, Q n e w ( s t , a t ) ← Q ( s t , a t ) + α ⋅ ( r t + γ ⋅ m a x a Q ( s t + 1 , a ) − Q ( s t , a t ) ) Q^{new}(s_t,a_t) \leftarrow Q(s_t,a_t) + \alpha \cdot (r_t + \gamma \cdot max_aQ(s_{t+1},a) - Q(s_t,a_t)) Qnew(st,at)←Q(st,at)+α⋅(rt+γ⋅maxaQ(st+1,a)−Q(st,at))
其中, α = 0.2 , γ = 0.1 \alpha = 0.2, \gamma = 0.1 α=0.2,γ=0.1。
Step1. 初始化 Q-Table:
| state \ action | 上 | 右 | 下 | 左 |
|---|---|---|---|---|
| START | 0 | 0 | 0 | 0 |
| BLANK | 0 | 0 | 0 | 0 |
| CAKE | 0 | 0 | 0 | 0 |
| SUN | 0 | 0 | 0 | 0 |
| BOMB | 0 | 0 | 0 | 0 |
| EXIT | 0 | 0 | 0 | 0 |
Step2. 更新 Q_table,其中 ϵ = 0.1 \epsilon=0.1 ϵ=0.1。
两轮如下:
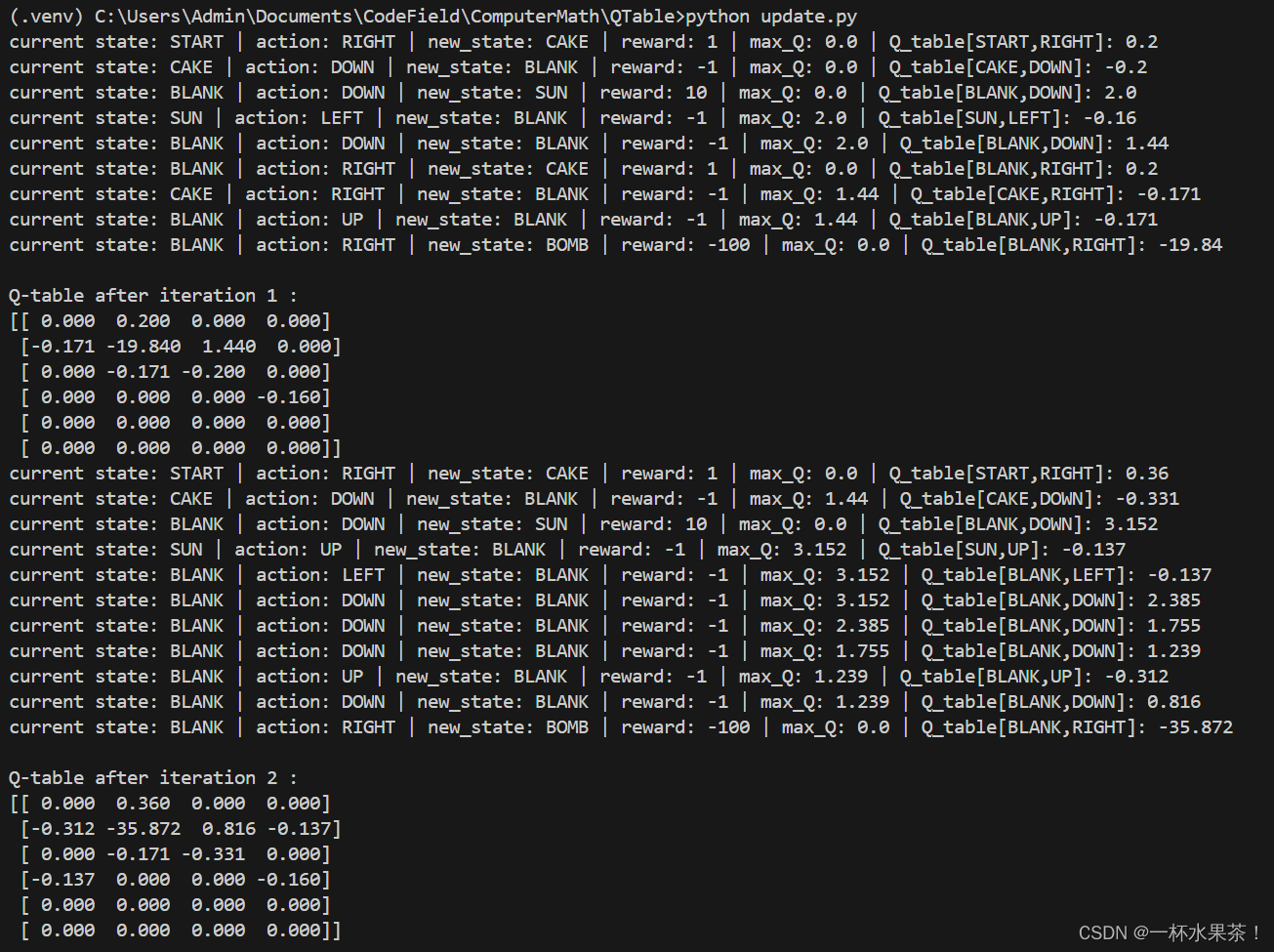
第一轮中第一列计算过程:
Q
n
e
w
(
B
L
A
N
K
,
U
P
)
=
0
+
0.2
∗
(
−
1
+
0.1
∗
1.44
−
0
)
=
−
0.171
Q^{new}(BLANK,UP) = 0 + 0.2*(-1 + 0.1* 1.44 - 0) = -0.171
Qnew(BLANK,UP)=0+0.2∗(−1+0.1∗1.44−0)=−0.171
第二轮第一列计算过程:
Q
n
e
w
(
S
U
N
,
U
P
)
=
0
+
0.2
∗
(
−
1
+
0.1
∗
3.152
−
0
)
=
−
0.137
Q
n
e
w
(
B
L
A
N
K
,
U
P
)
=
−
0.171
+
0.2
∗
(
−
1
+
0.1
∗
1.239
+
0.171
)
=
−
0.312
\begin{aligned} Q^{new}(SUN,UP) &= 0 + 0.2*(-1 + 0.1* 3.152 - 0) = -0.137 \\ Q^{new}(BLANK,UP) &= -0.171 + 0.2*(-1 + 0.1* 1.239 + 0.171) = -0.312 \\ \end{aligned}
Qnew(SUN,UP)Qnew(BLANK,UP)=0+0.2∗(−1+0.1∗3.152−0)=−0.137=−0.171+0.2∗(−1+0.1∗1.239+0.171)=−0.312
- 假设有四个观测点,分别为(-4,-0.55), (1, 0.45) , (-0.5, 0.22)和(5,1.25),⽤最⼩⼆乘法求解直线 y = a x + b y=ax+b y=ax+b 使其最佳拟合这些散点。给出求解过程。
【解】
方法一:
建立模型如下,
m
i
n
a
,
b
f
(
a
,
b
)
=
∑
i
=
1
n
(
a
x
i
+
b
−
y
i
)
2
min_{a,b}f(a,b) = \sum_{i=1}^n(ax_i+b-y_i)^2
mina,bf(a,b)=i=1∑n(axi+b−yi)2
分别对
a
,
b
a,b
a,b 进行求偏导数,并令其为 0,
{
∂
f
∂
a
=
2
∑
i
=
1
n
x
i
(
a
x
i
+
b
−
y
i
)
=
0
∂
f
∂
b
=
2
∑
i
=
1
n
(
a
x
i
+
b
−
y
i
)
=
0
\begin{cases} \frac{\partial f}{\partial a} = 2 \sum_{i=1}^{n} x_i(ax_i + b-y_i)=0 \\ \frac{\partial f}{\partial b} = 2 \sum_{i=1}^{n} (ax_i + b -y_i)=0 \end{cases}
{∂a∂f=2∑i=1nxi(axi+b−yi)=0∂b∂f=2∑i=1n(axi+b−yi)=0
化简可得解为:
a
^
=
n
∑
i
=
1
n
x
i
y
i
−
∑
i
=
1
n
x
i
∑
i
=
1
n
y
i
n
∑
i
=
1
n
x
i
2
−
(
∑
i
=
1
n
x
i
)
2
b
^
=
(
∑
i
=
1
n
y
i
)
−
a
(
∑
i
=
1
n
x
i
)
n
\begin{aligned} \hat{a} &= \frac{n\sum_{i=1}^n x_i y_i - \sum_{i=1}^n x_i \sum_{i=1}^n y_i}{n\sum_{i=1}^n x_i^2 - (\sum_{i=1}^n x_i)^2} \\ \hat{b} &= \frac{(\sum_{i=1}^n y_i) - a(\sum_{i=1}^n x_i)}{n} \\ \end{aligned}
a^b^=n∑i=1nxi2−(∑i=1nxi)2n∑i=1nxiyi−∑i=1nxi∑i=1nyi=n(∑i=1nyi)−a(∑i=1nxi)
将以下值代入上述公式,
∑
i
=
1
4
x
i
=
−
4
+
1
−
0.5
+
5
=
1.5
∑
i
=
1
4
y
i
=
−
0.55
+
0.45
+
0.22
+
1.25
=
1.37
∑
i
=
1
4
x
i
y
i
=
(
−
4
)
(
−
0.55
)
+
1
×
0.45
+
(
−
0.5
)
×
0.22
+
5
×
1.25
=
8.79
∑
i
=
1
4
x
i
2
=
(
−
4
)
2
+
(
1
)
2
+
(
−
0.5
)
2
+
(
5
)
2
=
42.25
\begin{aligned} \sum_{i=1}^4 x_i &= -4 + 1 - 0.5 + 5 = 1.5 \\ \sum_{i=1}^4 y_i &= -0.55 + 0.45 + 0.22 + 1.25 = 1.37 \\ \sum_{i=1}^4 x_i y_i &= (-4)(-0.55) + 1×0.45 + (-0.5)×0.22 + 5×1.25 = 8.79 \\ \sum_{i=1}^4 x_i^2 &= (-4)^2 + (1)^2 + (-0.5)^2 + (5)^2 = 42.25 \\ \end{aligned}
i=1∑4xii=1∑4yii=1∑4xiyii=1∑4xi2=−4+1−0.5+5=1.5=−0.55+0.45+0.22+1.25=1.37=(−4)(−0.55)+1×0.45+(−0.5)×0.22+5×1.25=8.79=(−4)2+(1)2+(−0.5)2+(5)2=42.25
得,
a
^
=
4
×
8.79
−
1.5
×
1.37
4
×
42.25
−
1.
5
2
=
0.1985
b
^
=
1.37
−
0.1985
×
1.5
4
=
0.2681
\begin{aligned} \hat{a} &= \frac{4 \times 8.79 - 1.5 \times 1.37 }{4 \times 42.25 - 1.5^2} = 0.1985 \\ \hat{b} &= \frac{1.37 - 0.1985 \times 1.5}{4} = 0.2681 \end{aligned}
a^b^=4×42.25−1.524×8.79−1.5×1.37=0.1985=41.37−0.1985×1.5=0.2681
方法二:
θ = ( X T X ) − 1 X T y \theta = (\mathbf X^T \mathbf X)^{-1} \mathbf X^Ty θ=(XTX)−1XTy
编程题
说明:建议使⽤开源⼯具包,例如 scikit-learn 中有朴素⻉叶斯、⾼斯混合模型等函数实现, sknetwork 中有 PageRank 函数实现。
Node2vec 数据集:PageRank_Dataset.csv。
任务描述:利⽤ Node2vec 计算每个节点的 embedding 值。
要求输出:
1)每个节点的 embedding 值列表(csv ⽂件);
2)随机挑选 10 个 node pair,对⽐他们在 embedding 上的相似度和在 betweenness centrality 上的相似度(使⽤ Jaccard similarity)。
代码如下:
import pandas as pd
import networkx as nx
from node2vec import Node2Vec
from sklearn.metrics.pairwise import cosine_similarity
from sklearn.preprocessing import MinMaxScaler
# Load the dataset
data = pd.read_csv('PageRank_Dataset.csv')
# Create a graph from the dataset
graph = nx.from_pandas_edgelist(data, source='node_1', target='node_2')
# Run Node2Vec to compute node embeddings
node2vec = Node2Vec(graph, dimensions=128, walk_length=30, num_walks=200, workers=4)
model = node2vec.fit(window=10, min_count=1, batch_words=4)
# Get embeddings for all nodes
embeddings = {}
for node in graph.nodes:
embeddings[node] = model.wv[node]
# Save the embeddings to a CSV file
df = pd.DataFrame.from_dict(embeddings, orient='index')
df.to_csv('node_embeddings.csv')
# Randomly select 10 node pairs
node_pairs = data.sample(n=10)[['node_1', 'node_2']]
# Compute similarity based on embeddings
similarity_embeddings = []
for _, row in node_pairs.iterrows():
source_embedding = embeddings[row['node_1']]
target_embedding = embeddings[row['node_2']]
similarity = cosine_similarity([source_embedding], [target_embedding])[0][0]
similarity_embeddings.append(similarity)
# Compute similarity based on betweenness centrality
betweenness_centrality = nx.betweenness_centrality(graph)
similarity_betweenness = []
for _, row in node_pairs.iterrows():
source_betweenness = betweenness_centrality[row['node_1']]
target_betweenness = betweenness_centrality[row['node_2']]
jaccard_similarity = len(set(nx.neighbors(graph, row['node_1'])).intersection(nx.neighbors(graph, row['node_2']))) / \
len(set(nx.neighbors(graph, row['node_1'])).union(nx.neighbors(graph, row['node_2'])))
similarity_betweenness.append(jaccard_similarity)
# Print the similarities
for i in range(len(node_pairs)):
print(f"Node Pair {i+1}:")
print(f"Similarity based on embeddings: {similarity_embeddings[i]}")
print(f"Similarity based on betweenness centrality: {similarity_betweenness[i]}")
print()
每个节点的 embedding 值列表(csv ⽂件)见附件 Node_Embeddings.csv。
10 个 node pair 的相似度如下:
Node Pair 1:
Similarity based on embeddings: 0.2817123532295227
Similarity based on betweenness centrality: 0.0
Node Pair 2:
Similarity based on embeddings: 0.15493448078632355
Similarity based on betweenness centrality: 0.0
Node Pair 3:
Similarity based on embeddings: 0.20358529686927795
Similarity based on betweenness centrality: 0.022099447513812154
Node Pair 4:
Similarity based on embeddings: 0.15917743742465973
Similarity based on betweenness centrality: 0.0
Node Pair 5:
Similarity based on embeddings: 0.20524653792381287
Similarity based on betweenness centrality: 0.02702702702702703
Node Pair 6:
Similarity based on embeddings: 0.09693200141191483
Similarity based on betweenness centrality: 0.15517241379310345
Node Pair 7:
Similarity based on embeddings: 0.1875799596309662
Similarity based on betweenness centrality: 0.2608695652173913
Node Pair 8:
Similarity based on embeddings: 0.24301061034202576
Similarity based on betweenness centrality: 0.0
Node Pair 9:
Similarity based on embeddings: 0.5237224102020264
Similarity based on betweenness centrality: 0.23529411764705882
Node Pair 10:
Similarity based on embeddings: 0.20514701306819916
Similarity based on betweenness centrality: 0.26785714285714285






![YOLOv8数据集可视化[目标检测实践篇]](https://i-blog.csdnimg.cn/direct/4605f4bf1f2f4f0f90e6e76123685806.png)