Overview

What you’ll be able to do!

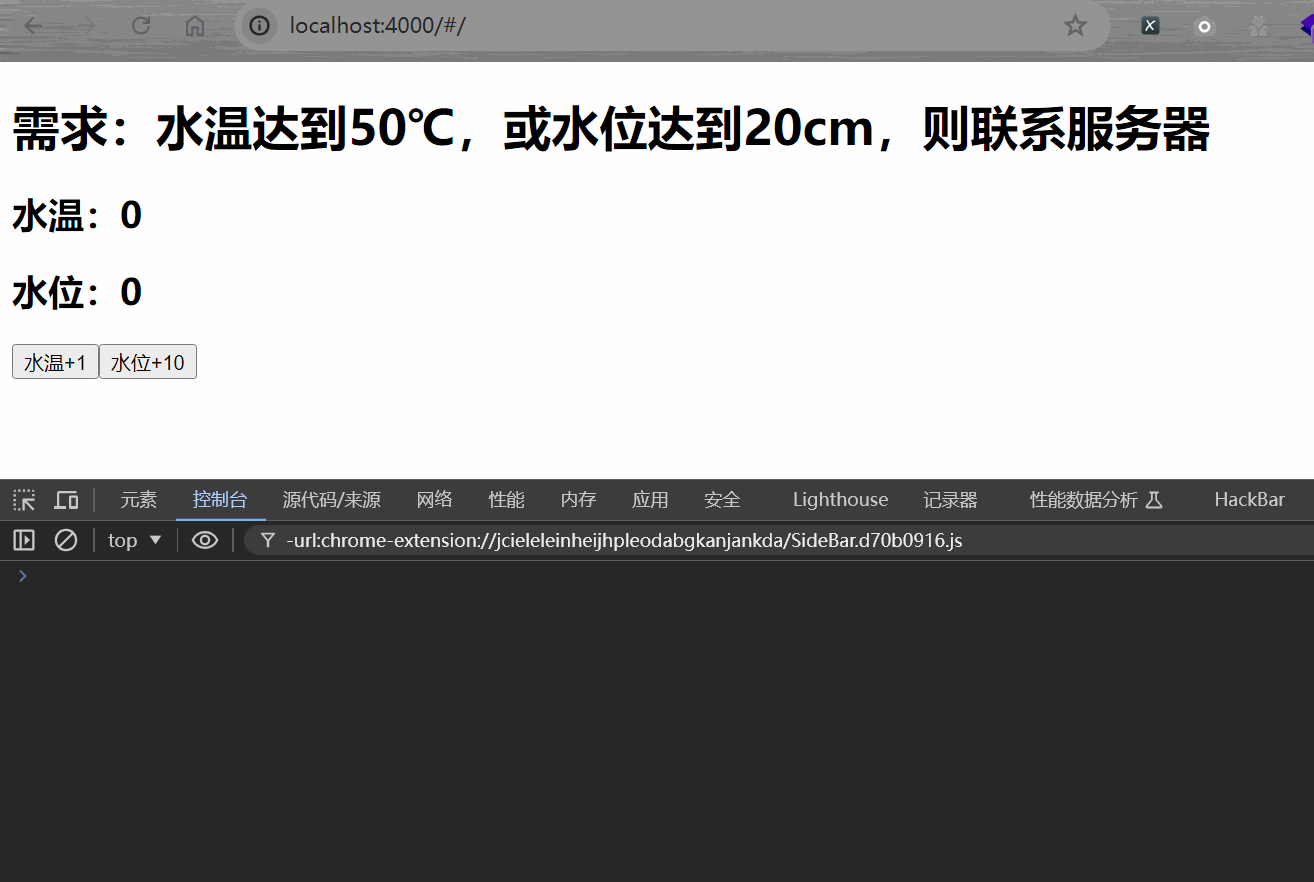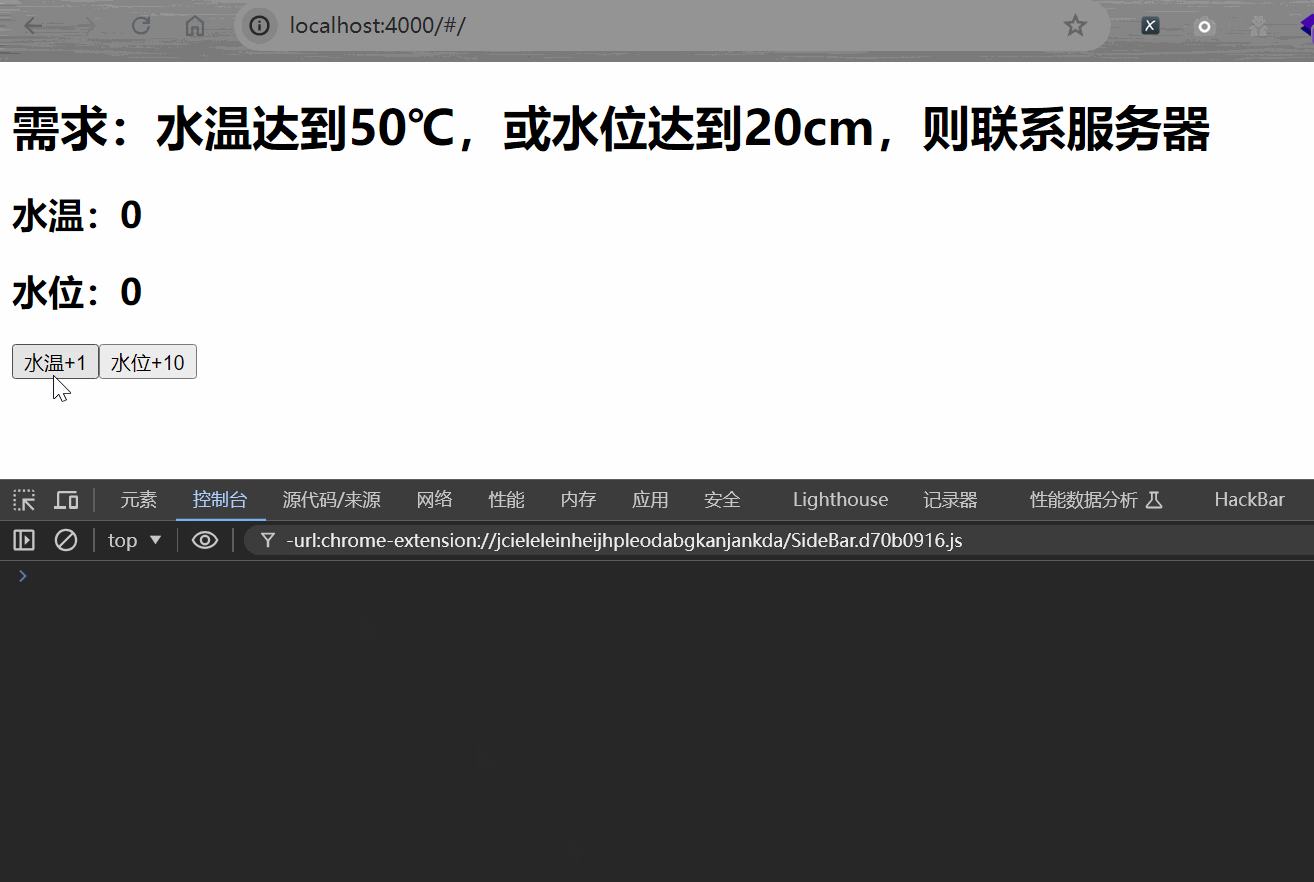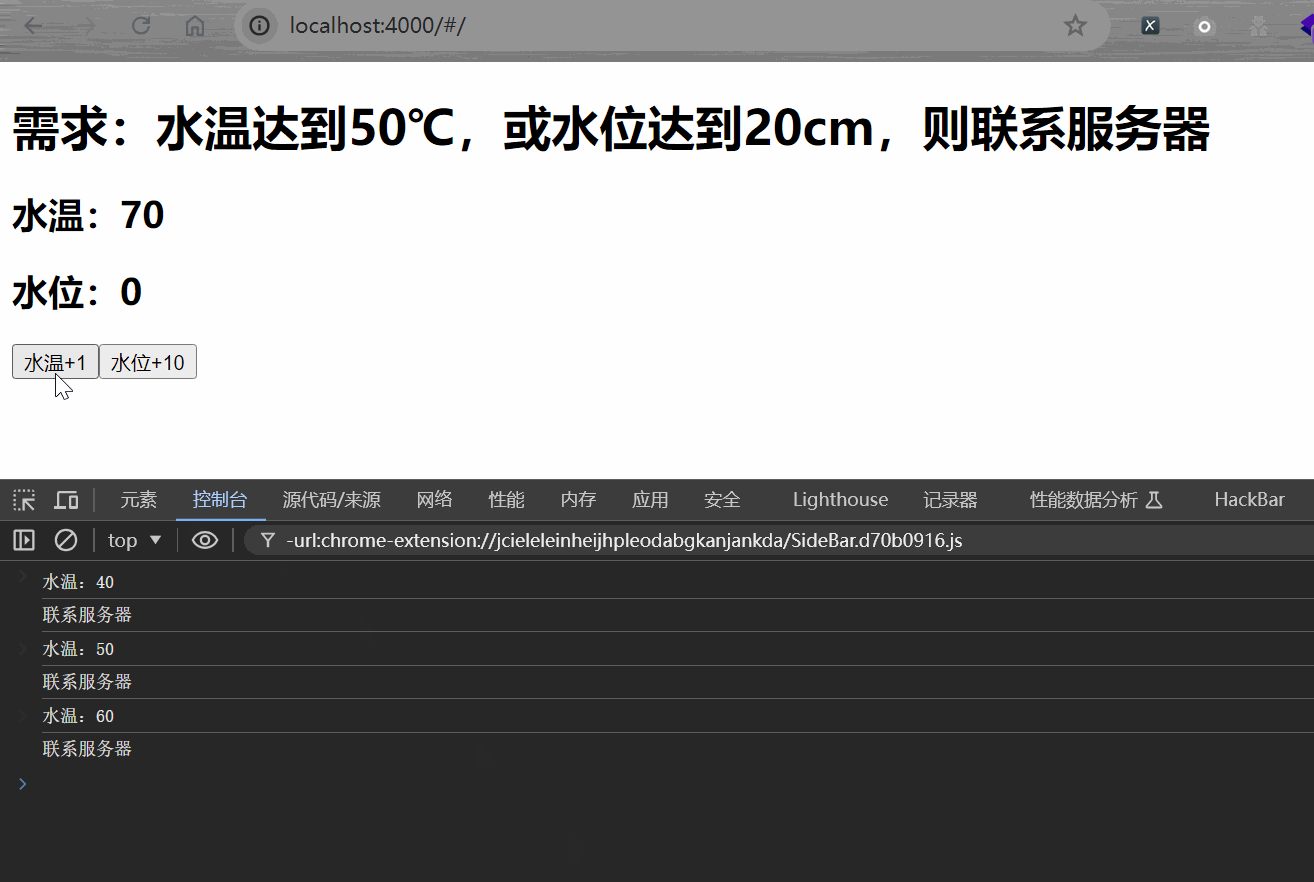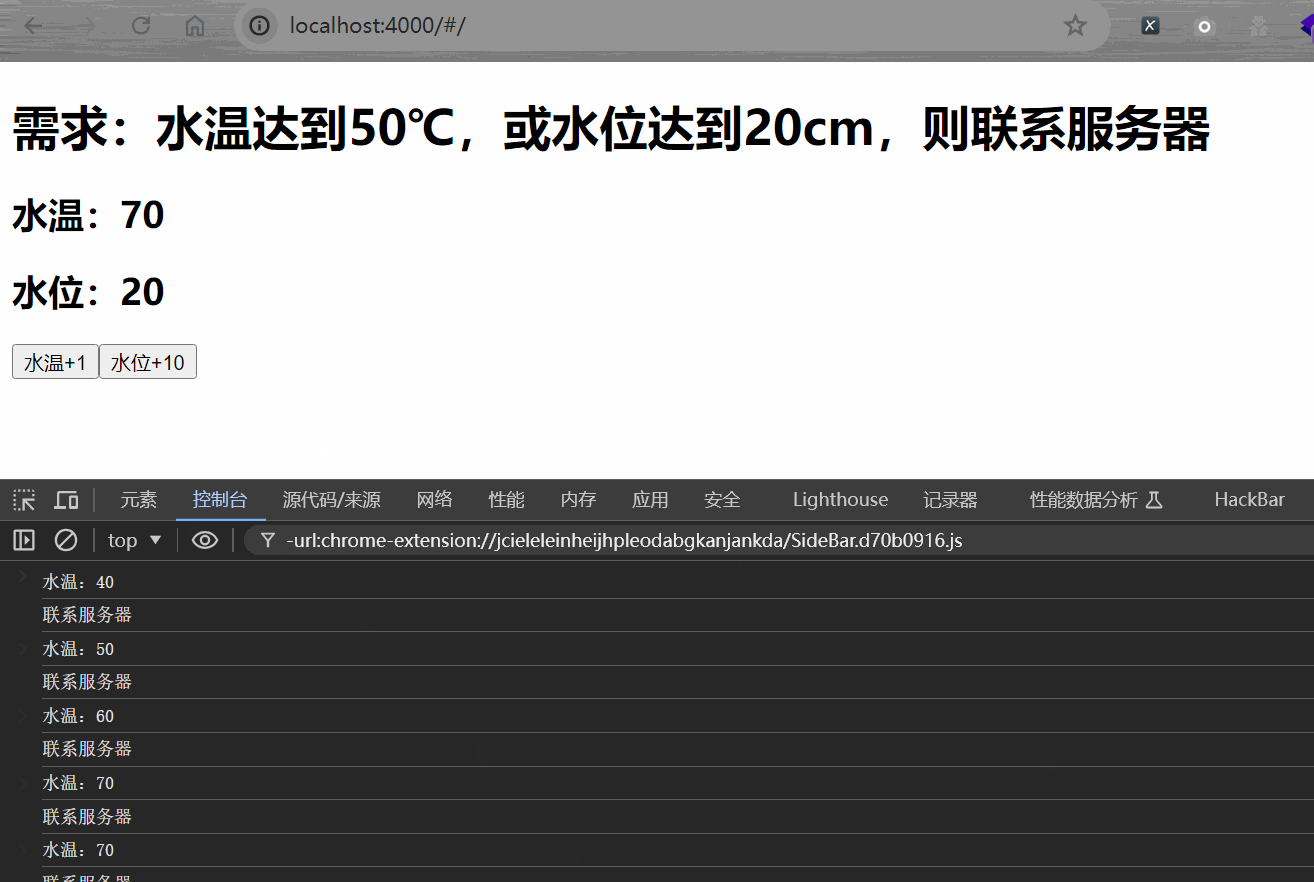
machine translation，例如，英文→法文
document search，例如，根据给定句子：“Can I get a refund?”
搜索文档类似内容：
“What’s your return policy?”
“May I get my money back?”

Learning Objectives

“Transform vector”：转换向量
“K nearest neighbor”：K 最近邻
“Hash tables”：哈希表
“Divide vector space into regions”：将向量空间划分为区域
“Locality sensitive hashing”：局部敏感哈希
“Approximated nearest neighbors”：近似最近邻

Transforming word vectors

Overview of Translation

这里以英语翻译法语为例。

最笨的方法就是做一个英文与法文对应的列表。
如果要使用计算机来进行翻译，
先要将英文和法文的词向量表示给出来：

然后检索要翻译单词的词向量，如cat

将英文单词词向量转化为法文单词空间词向量：

在法语词向量空间中找到与转化结果最接近（相似）的词向量，最相似的单词就是翻译的候选单词，例如找到chat，就是法语中的cat

这里涉及到的Transform是用Matrix来完成的。

Transforming vectors

R = np. array([[2,0],[0,2]])
x = np. array([[1,1]])
np.dot(x,R)

最后结果：array([[2,2]])，从图像上看是这样的：

既然有向量$R$使得英文词向量能转化为法文词向量，那我们来看看如何找到它。

Align word vectors

我们可以先随机初始化$R$，然后查看转化的效果与实际法语词向量的差异。
首先要做的是对齐词向量，就是从词库中选择部分词（subsets of the full vocabulary），构造如下两个对齐向量：

每一行都是对应英法语的对应。

Solving for R

initialize R
in a loop:
$$Loss=||XR-Y|{|}_F$$
$$g=\frac{d}{dR}Lossgradient$$
$$R=R-\alpha gupdate$$
以上步骤中，损失函数求的是预测值$XR$与实际值$Y$之间的差异，我们希望差异越小越好，使用GD进行求解。
损失函数的下标F代表Frobenius范数，求法看下面

Frobenius norm

Frobenius范数是一种在矩阵理论中常用的范数，它定义为矩阵元素平方和的平方根。具体来说，对于一个$m\times n$的矩阵$A$，其Frobenius范数表示为：
$$\Vert A{\Vert }_F=\sqrt{\sum _{i=1}^m\sum _{j=1}^n|a_{ij}{|}^2}$$
robenius范数有时也被称为希尔伯特-施密特范数（Hilbert-Schmidt norm）
例子，假设我们只有2个单词，则矩阵有2行，词向量是2维的，则矩阵有2列，$XR-Y$的结果也是一个矩阵，记为$A$，矩阵$X、R、Y$和$A$都是2乘2的矩阵，假设：
$$A=\left(\begin{array}{cc}2& 2\\ 2& 2\end{array}\right)$$
$$\Vert A{\Vert }_F=\sqrt{2^2+2^2+2^2+2^2}=4$$

A = np.array([[2,2],[2,2]])
A_squared = np.square(A)
A_squared

结果：array([[4,4],[4,4]])

A_Frobenious= np.sqrt(np.sum(A_squared))
A_Frobenious

结果：4

Frobenius norm squared

$$||XR-Y|{|}_F^2$$
加上平方会让计算更加方便，去掉根号：
$$A=\left(\begin{array}{cc}2& 2\\ 2& 2\end{array}\right)$$
$$\Vert A{\Vert }_F^2=(\sqrt{2^2+2^2+2^2+2^2}{)}^2=16$$

Gradient

加上平方后，新的损失函数变成：
$$Loss=||XR-Y|{|}_F^2$$
通过GD计算最小化Loss，变成求偏导操作：
$$g=\frac{d}{dR}Loss=\frac{2}{m}(X^T(XR-Y))$$

K nearest neighbors

Finding the translation

在翻译英法语言过程中，我们通过R矩阵进行变换，得到的结果不一定与法语词向量空间中的单词完全对应：

这个时候需要我们找到最相近的词向量：

Nearest neighbours

先来看一个找朋友的例子，假设你住在三藩市，要找到最近的朋友：

Bangalore是印度的班加罗尔。
当你的朋友很多的时候，找到最邻近的朋友可能是一个非常耗时的过程。
可以考虑缩写查找范围，例如上例中我们可以将查找范围缩小到美国所在的北美洲过滤掉无关人员。
对于最邻近算法，可以设定一个搜索范围，有效提高算法效率。接下来我们将学习使用哈希表来组织数据集子集。

Hash tables and hash functions

Hash tables

假设有多个数据项，我们想通过某种相似性将它们分组到桶中

规则：
一个桶可有多个数据项
一个数据项属于某个桶
结果：

Hash function

其实这块在数据结构中有学过。
对于词向量而言，我们先从一维词向量来看，也就是单个数字，例如：
$$100,14,17,10,97$$
这里我们定义哈希函数来得到哈希值，并用哈希值来决定向量放入哪个桶中。

假设我们有10个桶，并将哈希函数定义为：

那么存放结果为：

Create a basic hash table

将以上内容编程实现：定义一个名为 basic_hash_table 的函数，用于创建一个基本的哈希表。这个哈希表使用一个列表来存储值，并使用一个简单的哈希函数来确定每个值应该存储在哈希表的哪个位置（即“桶”）。

def basic_hash_table(value_l, n_buckets):
    # 定义哈希函数，使用整数除法的余数来确定桶的位置
    def hash_function(value, n_buckets):
        return int(value) % n_buckets
    
    # 创建一个哈希表，其中包含n_buckets个空列表作为桶
    hash_table = {i: [] for i in range(n_buckets)}
    
    # 遍历输入值列表value_l
    for value in value_l:
        # 对每个值使用哈希函数计算其哈希值
        hash_value = hash_function(value, n_buckets)
        
        # 将值添加到对应的桶中
        hash_table[hash_value].append(value)
    
    # 返回填充好的哈希表
    return hash_table

# 使用示例：
# values = [1, 2, 3, 4, 5, 6, 7, 8, 9, 10]
# num_buckets = 3
# hash_table = basic_hash_table(values, num_buckets)
# print(hash_table)

注意：这段代码中的哈希函数非常简单，它只是取输入值的整数形式然后对桶的数量进行取模操作。这可能导致不同的输入值映射到同一个桶中，这种现象称为哈希冲突。在实际应用中，可能需要更复杂的哈希函数和冲突解决策略来提高哈希表的性能。

Hash function v2

之前的哈希函数并没有使得相近的数字在一个桶中，这样并不满足我们的计算邻近算法的要求，我们希望哈希表结果如下（Locality sensitive hashing）：

Locality sensitive hashing

我们使用点来表示向量，并假设我们希望找到一种方法来使得蓝色、灰色向量是强相关的：

这里使用虚线来进行划分，但这些线称为Plane

可以看到，蓝色点在蓝色虚线的一侧，灰色点在灰色虚线的一侧。

也就是说这个划分方式是Locality sensitive的。

Planes

虽然在二维平面上，这里是一条紫色虚线，但是它实际上代表了所有可能位于该平面上的向量。例如下图中的橙色和蓝色向量

而紫色那个垂直于平面的，是法向量。
从三维空间上看，两个绿色向量组成一个平面，铅笔是法向量：

Which side of the plane?

在二维平面中如何判断向量和平面的位置呢？假设有三个示例向量和一个法向量P

分别求三个示例向量和法向量P的点积：
$$\begin{gathered} P{V}_1^T=3 \\ P{V}_2^T=0 \\ P{V}_3^T=-3 \end{gathered}$$
总结来说，这三个示例向量与法向量 P 的点积结果表明它们与 P 之间的角度关系分别是锐角、直角和钝角。
第二示例向量是在平面内，而其他两个分别在平面上和下面。

def side_of_plane (P,v):
	dotproduct = np. dot (P,v.T)
	sign_of_dot_product = np.sign(dotproduct)
	sign_of_dot_product_scalar = np.asscalar(sign_of_dot_product）
	return sign_of_dot_product_scalar

Visualizing a dot product

查看$V_1$到向量P的投影，实际上是求$||P{V}_1^T||$

如果对另外一个向量进行投影，则会得到负值，这里的notation和前面不一样，要注意。

也就是说正负符号代表了向量相对法向量的位置，也决定了向量在平面的哪一侧。

Multiple Planes

由于正负号决定了向量所处平面的位置，因此可以用多个平面来确定某个哈希值。

从上图可知，通过每个区域的不同信号，可以确定当前向量所处的位置。划分这些区域的过程就是哈希函数，通过哈希函数可以确定哈希值。
例如对于三个平面，某向量对它们的相对位置可以用以下方式计算，注意框框颜色与平面颜色对应：

该向量的hash值为：
$$hash=2^0\times h_1+2^1\times h_2+2^2\times h_3=1\times 1+2\times 1+4\times 0=3$$
通用的判定写法为：
$$\begin{gathered} sig{n}_i\ge 0,\to h_i=1 \\ sig{n}_i<0,\to h_i=0 \end{gathered}$$
最终hash值公式：
$$hash=\sum _i^H{2}^i\times h_i$$
代码：

def hash_multiple_plane (P_l,v)
	hash_value = 0
	for i, P in enumerate (P_l):
		sign = side_of_plane(P,v)
		hash_i = 1 if sign >= 0 else 0
		hash_value+=2**i*hash_i
	return hash_value 

Approximate nearest neighbors

Random Planes

在近似最近邻（Approximate Nearest Neighbors，简称ANN）的搜索算法中，“Random Planes” 通常指的是一种基于随机划分空间的方法，用于加速搜索过程。这种方法在一些ANN算法中被用来减少搜索空间，例如在局部敏感哈希（Locality-Sensitive Hashing，LSH）算法中。

在Random Planes方法中，随机平面的组数取决于具体的算法实现和参数设置。在某些实现中，可能只使用一组随机平面来划分空间，而在其他更复杂的实现中，可能会使用多组随机平面。使用多组随机平面可以提高搜索的准确性，因为它们可以从不同的角度对空间进行划分，从而增加找到真正最近邻的可能性。

可将不同组的Random Planes看做是不同的平行宇宙。

Multiple sets of random planes

假设我们将英法翻译得到词向量用紫色表示，然后使用了三组不同的随机平面进行划分，得到最紫色向量最邻近的结果也有三组，分别用三种颜色表示。

可以看到，不同组的平面划分得到结果也不一样，这种划分方法在紫色向量找朋友的时候没有与所有的其他向量进行比较，只比较了子集，因此只能称为：Approximate nearest (friendly) neighbors算法
假设词向量有2个维度，要生成三个随机平面：

num_dimensions = 2 #300 in assignment
num_planes = 3 #10 in assignment
random_planes_matrix = np. random.normal(size=(num_planes,num_dimensions))

结果：
array([[ 1.76405235 0.40015721]
[ 0.97873798 2.2408932 ]
[ 1.86755799 0.97727788]])
然后判断向量处于平面集合的哪个位置：

v = np. array([[ 2,2]])

然后判断向量位置：

def side_of_plane_matrix (P, v):
	dotproduct = np. dot (P, v.T)
	sign_of_dot_product=np.sign(dotproduct)
num_planes_matrix = side_of_plane_matrix(random_planes_matrix,v)

结果
array([[1.]
[1.]
[1.])

Searching documents

对应文档有以下句子：
I love learning!
其对应的文档向量表示可以从各个单词的sum得来

word_embedding = {"I": np.array([1,0,1]),
"love": np.array([-1,0,1]),
"learning": np.array([1,0,1]),

words_in_document = ['I', 'love', 'learning']
document_embedding= np. array ([0 0 0])
for word ind words_in_document:
	document_embedding+=
print(document_embedding)