到目前为止,我们主要讨论了等位基因和基因型频率,以及我们如何可以从一个推断出另一个。但是,如果我们不知道等位基因频率,只知道种群中存在哪些表型呢?如果我们足够幸运,知道哪些表型对应哪些基因型,我们可以很容易地估计等位基因频率!
前面的内容可以先看我之前的博客内容:群体遗传学_tRNA做科研的博客-CSDN博客
从表型计算等位基因频率
让我们考虑不同的血型作为一个简单的例子。人类通常只能有四种主要的血型:A、B、AB和O。这些血型中的每一个都对应于带有等位基因a、b或i的某种基因型:我们通过下表看一下不同血型对应的基因型
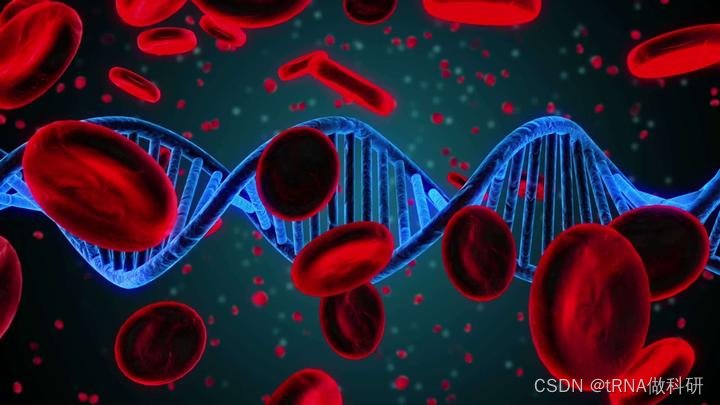
| 血型 | A | B | O | AB |
| 基因型 | aa或者ai | bb或者bi | 只能是ii | 只能是ab |
假设我们感兴趣的是找出a、b和i等位基因的比例。我们将使用先前确定的样本个体的血型(表型)(Nikolic等人,2010)我们样本中的表型比例可以通过将每种血型的数量除以个体总数(N)来找到:
AB <- 5
A <- 30
B <- 7
O <- 36
(N <- AB + A + B + O)
A/N
#[1] 0.3846154
B/N
#[1] 0.08974359
AB/N
#[1] 0.06410256
O/N
#[1] 0.4615385所以,大约38%的样本具有A型血表型,约9%为B型血,仅约6%为AB型血,而大约46%为O型血。这似乎并没有告诉我们太多关于a、b和i等位基因本身的总体频率,但找到表型比例是一个很好的第一步。还记得基于哈代-温伯格比例的预期基因型计算吗?我们已经知道O型血只能有ii基因型,根据哈代-温伯格预测,我们期望ii基因型的数量应该是基础i等位基因频率的平方值(p²i)。因此,假设的i等位基因频率(pi)就是ii基因型总比例的平方根:
(Pi <- sqrt(O/N))请注意,我们只是从关注O型血表型开始,虽然A型和B型血表型也包含一定比例的i等位基因作为ai和bi杂合子,但我们理论上预期的ii纯合子数量不会受到另外两个等位基因“隐藏”i等位基因作为杂合子这一事实的影响。
请记住,我们假设哈代-温伯格假设的所有条件都在起作用(例如,等位基因的完全随机关联),因此理论比例仍然成立。因此,现在至少我们知道在我们的样本中,i等位基因的预期等位基因频率约为68%。这为我们开始计算a和b等位基因的频率提供了一个起点。我们可以在这里建立同样的方程,看看我们如何得到基因型aa、ai(A型血表型)和ii(O型血表型)的所有个体的频率。 因此,如果我们想求解我们的血型等位基因频率的方程,我们再次假设它是由哈代-温伯格比例正确表示的,我们需要pa以及pi。我们通过计算A型和O型的所有情况的基因型频率进行计算推导:
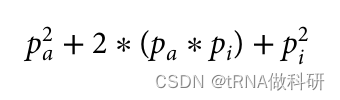
可以推为:
![]()
并且因为我们知道这个值仅仅是样本中A型和O型血型的总比例,我们可以使用我们已经收集到的表型值来找到它。
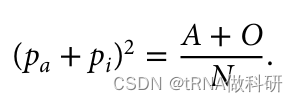
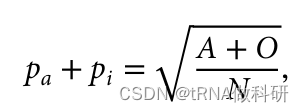
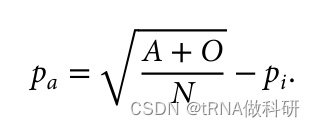
这样我们就从表型数据中计算得到了a的等位基因频率,同样的方式,我们也可以得到b的等位基因频率:我们通过R语言进行计算
(Pa <- sqrt((A+O)/N)-Pi)
(Pb <- sqrt((B+O)/N)-Pi)现在我们把三个基因频率进行加和:
Pa + Pb + Pi
#[1] 0.9829837我们发现合起来是一个不足1的数,但是很接近1
问题在于,表型频率与真正的哈代-温伯格预测相比略有偏差,我们在解决等位基因频率时,没有充分考虑到这种“张力”,而是独立于整体逐步进行的。为了帮助说明,这里是我们基于等位基因频率估计得出的AB杂合子的预测数量。 在哈代-温伯格原理下,如果等位基因频率分别为p和q,则AB血型的预期频率应该是2pq。然而,如果实际观察到的AB血型频率与这个预期值有所偏差,这可能表明存在一些违反哈代-温伯格原理假设的条件,比如非随机交配、自然选择、基因漂变或突变等。 当我们分别独立地计算每个等位基因频率时,我们可能没有充分考虑这些因素对整体等位基因频率分布的影响。因此,尽管我们可以使用表型频率来估计等位基因频率,但如果这些频率不完全符合哈代-温伯格平衡的预期,我们的估计就可能不够准确。 为了更全面地考虑这些“张力”,我们可能需要采用更复杂的统计方法或模型,这些方法能够同时考虑所有等位基因和表型频率之间的关系,以及可能影响这些频率的其他遗传和进化因素。这样,我们才能更准确地理解和解释观察到的遗传变异,并在必要时调整我们的等位基因频率估计。
最大似然估计
N*2*Pa*Pb
#[1] 2.368042然而,观察到的数量是这个值的两倍多。我们可以做得更好,编写一个算法来修改这些估计值,使其基于整个观察数据集的同时达到最大似然解。 在这种情况下,最大似然估计(MLE)是一种非常有用的方法。MLE的目标是找到一组参数值,使得在给定这些参数值的情况下,观察到当前数据集的概率最大化。在遗传学中,这意味着我们要找到一组等位基因频率,使得观察到的表型频率最有可能出现。 为了实现这一点,我们可以构建一个似然函数,该函数将观察到的表型频率与由特定等位基因频率预测的表型频率之间的差异作为输入。然后,我们可以使用优化算法(如梯度下降法)来调整等位基因频率,直到似然函数达到最大值。 这个过程通常涉及到以下几个步骤:
1. 根据观察到的表型频率初始化等位基因频率的估计值。
2. 构建似然函数,该函数衡量在给定当前等位基因频率估计值的情况下,观察到的表型频率出现的概率。
3. 使用优化算法(如梯度下降法)调整等位基因频率估计值,以最大化似然函数。
4. 重复步骤3,直到似然函数收敛到一个最大值,或者达到预定的迭代次数。
通过这种方式,我们可以得到一组更准确的等位基因频率估计值,这些估计值能够更好地反映整个数据集的信息,而不仅仅是单独的表型频率。这种方法有助于我们更准确地理解和解释遗传数据,特别是在表型频率不完全符合哈代-温伯格平衡预期的情况下,我们进行一个简单的例子,更为精准及复杂的例子看下面一节。
# 安装并加载必要的包
if (!requireNamespace("MASS", quietly = TRUE))
install.packages("MASS")
library(MASS)
# 定义似然函数
likelihood <- function(freqs, obs_freqs) {
p_A <- freqs[1]^2 + 2 * freqs[1] * freqs[3]
p_B <- freqs[2]^2 + 2 * freqs[2] * freqs[3]
p_AB <- 2 * freqs[1] * freqs[2]
p_O <- freqs[3]^2
# 计算似然值
like <- prod(dbinom(obs_freqs, rep(1, length(obs_freqs)), c(p_A, p_B, p_AB, p_O)))
return(like)
}
# 观察到的表型频率
obs_freqs <- c(0.38, 0.09, 0.06, 0.46)
# 初始化等位基因频率估计值
initial_freqs <- c(0.3, 0.2, 0.5)
# 使用优化算法寻找最大似然解
opt_freqs <- optim(par = initial_freqs, fn = likelihood, obs_freqs = obs_freqs, method = "BFGS")$par
# 输出结果
print(opt_freqs)期望值最大化算法(expectation maximization algorithm)
算法是一个大多数人熟悉但难以轻易定义的术语。这个词实际上来源于九世纪数学家Muh .ammad ibn Mūsā al-Khwārizmı(拉丁化的al-Khwārizmı被称为“Algorismus”)的名字,他也给我们带来了“代数”这个词(阿拉伯语中的al-jabr意味着“重新连接”或“完成”)。一个非常简单的定义是,算法就是一系列按特定顺序执行的操作。算法在大多数定量学科中非常标准,最近机器学习的算法类型已被应用于群体遗传学推断。机器学习最近在许多数据分析领域成为了一个热门话题,并经常被视为一种全新的方法。然而,许多传统使用的方法与机器学习的概念完全相同;也就是说,不断更新信息以得出更准确的结论。其中一种实现这一目标的方法被称为期望最大化(EM)算法。 之前,在我们的血型示例中,我们能够计算出在给定样本大小并假设我们处于哈代-温伯格平衡的情况下,我们会预期看到哪些基因型。
# 计算基因型频率 Paa
Paa <- A * (Pa^2 / (Pa^2 + 2 * Pa * Pi))
# 输出 Paa 的值
print(Paa)
# 计算基因型频率 Pai
Pai <- A * (2 * Pa * Pi / (Pa^2 + 2 * Pa * Pi))
# 输出 Pai 的值
print(Pai)
# 计算基因型频率 Pbb
Pbb <- B * (Pb^2 / (Pb^2 + 2 * Pb * Pi))
# 输出 Pbb 的值
print(Pbb)
# 计算基因型频率 Pbi
Pbi <- B * (2 * Pb * Pi / (Pb^2 + 2 * Pb * Pi))
# 输出 Pbi 的值
print(Pbi)
# 计算基因型频率 Pii,这里直接赋值为常数O
Pii <- O
# 输出 Pii 的值
print(Pii)
# 计算基因型频率 Pab,这里直接赋值为常数AB
Pab <- AB
# 输出 Pab 的值
print(Pab)现在我们可以通过哈代温伯格频率重新推算等位基因频率:
# 计算Pa的值
Pa <- ((2 * Paa) + Pai + Pab) / (2 * N)
Pa
# 计算Pb的值
Pb <- ((2 * Pbb) + Pbi + Pab) / (2 * N)
Pb
# 计算Pi的值
Pi <- ((2 * Pii) + Pai + Pbi) / (2 * N)
Pi再通过我们重新计算的等位基因频率去反推基因型频率:
# 计算Paa的值
Paa <- A * (Pa^2 / (Pa^2 + 2 * Pa * Pi))
Paa
# 计算Pai的值
Pai <- A * (2 * Pa * Pi / (Pa^2 + 2 * Pa * Pi))
Pai
# 计算Pbb的值
Pbb <- B * (Pb^2 / (Pb^2 + 2 * Pb * Pi))
Pbb
# 计算Pbi的值
Pbi <- B * (2 * Pb * Pi / (Pb^2 + 2 * Pb * Pi))
Pbi然后我们可以一次又一次地重新估计等位基因频率,直到我们收敛到等位基因频率的最大似然值。
现在我们可以开始重新编写实际的函数来帮助我们进行最大似然估计。
# 清除工作空间
rm(list = ls())
# 初始化变量
# AB: AB血型个体数量
# A: A血型个体数量
# B: B血型个体数量
# O: O血型个体数量
# N: 总个体数量
# Pi: O血型基因频率
# Pa: A血型基因频率
# Pb: B血型基因频率
# Pi0, Pa0, Pb0: 上一次迭代的基因频率
# counter: 迭代次数
AB <- 5
A <- 30
B <- 7
O <- 36
N <- AB + A + B + O
Pi <- sqrt(O / N)
Pa <- sqrt((A + O) / N) - Pi
Pb <- sqrt((B + O) / N) - Pi
Pi0 <- 0
Pa0 <- 0
Pb0 <- 0
counter <- 0
# 定义EM函数
# 该函数使用期望最大化(EM)算法来估计基因频率
EM <- function(Pi, Pa, Pb){
# 当基因频率的变化小于一定阈值时停止迭代
while((round(Pi0, 12) != round(Pi, 12)) ||
(round(Pa0, 12) != round(Pa, 12)) ||
(round(Pb0, 12) != round(Pb, 12))){
Pi0 <- Pi
Pa0 <- Pa
Pb0 <- Pb
# 根据上一次迭代的基因频率计算新的基因频率
Paa <- A * (Pa0^2 / (Pa0^2 + 2 * Pa0 * Pi0)) # A血型个体的AA基因型频率
Pai <- A * (2 * Pa0 * Pi0 / (Pa0^2 + 2 * Pa0 * Pi0)) # A血型个体的AO基因型频率
Pbb <- B * (Pb0^2 / (Pb0^2 + 2 * Pb0 * Pi0)) # B血型个体的BB基因型频率
Pbi <- B * (2 * Pb0 * Pi0 / (Pb0^2 + 2 * Pb0 * Pi0)) # B血型个体的BO基因型频率
Pii <- O # O血型个体的OO基因型频率
Pab <- AB # AB血型个体的AB基因型频率
# 更新基因频率
Pa <- ((2 * Paa) + Pai + Pab) / (2 * N)
Pb <- ((2 * Pbb) + Pbi + Pab) / (2 * N)
Pi <- ((2 * Pii) + Pai + Pbi) / (2 * N)
# 增加迭代次数
counter <- counter + 1
}
# 返回最终的基因频率和迭代次数
return(c(paste("Pi =", Pi, ", Pa =", Pa, ", Pb=", Pb, ", Number of loops =", counter)))
}
# 调用EM函数
EM(Pi, Pa, Pb)
c(Pi, Pa, Pb) # Our initial estimates

可以得到估计完后和为1。
即使我们有任意的起始等位基因频率,比如pi = pa = pb = 1/3,算法仍然应该快速收敛到这些相同的值。到目前为止,我们主要关注的是固定时间点的数据集,并且主要是将等位基因频率的样本与基于无限大的理论种群的预测进行比较。在下一篇博客中,我们将开始研究有限种群以及随时间变化的等位基因频率。
谢谢大家的点赞关注收藏!