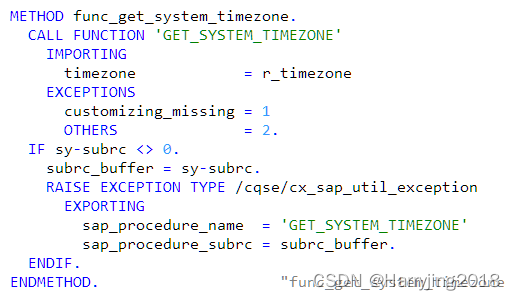
A.三角形
判断等边三角形,题不难,代码如下:
#include <iostream>
using namespace std;
int a[110];
int main()
{
int n;
cin >> n;
int x;
int mx = 0;
for(int i = 1; i <= n; i++)
{
cin >> x;
mx = max(mx, x);
a[x]++;
}
for(int i = 1; i <= mx; i++)
if(a[i] >= 3)
{
cout << "YES" << endl;
return 0;
}
cout << "NO" << endl;
return 0;
}B.好数组
分析:因为0<= <= 1e9,如果要满足
,那么
就只能大于0,如果取到等于0,带入下就会发现不合适,因此只要数组中存在等于零的数,那就不是一个好数组,代码如下:
#include <iostream>
using namespace std;
int main()
{
int n;
cin >> n;
int x;
cin >> x;
bool f = 0;
for(int i = 1; i <= n; i++)
{
cin >> x;
if(!x) f = 1;//判断x是否为0
}
if(f) cout << "NO" << endl;
else cout << "YES" << endl;
return 0;
}C.前缀平方和序列
分析:我们需要在x的范围内去找n个平方数,如果x的范围内有a个平方数,那么找到的平方数的种类就是,数据范围只有1e3,因此我们可以用杨辉三角直接递推,代码如下:
#include <iostream>
#include <math.h>
using namespace std;
const int N = 1010, mod = 1e9+7;
int c[N][N];
int main()
{
int n, x;
cin >> n >> x;
for(int i = 0; i < N; i++)
{
for(int j = 0; j <= i; j++)
{
if(!j) c[i][j] = 1;
else c[i][j] = (c[i - 1][j - 1] + c[i - 1][j]) % mod;
}
}
int a = pow(x, 1.0/2);//确定x范围内有多少个平方数
cout << c[a][n] << endl;
return 0;
}D.走一个大整数迷宫
分析:这个题的只是一个幌子,我想了半天没想出来要怎么去求出来这个数,为什么要说是幌子呢?因为这个数最终要对(p-1)取模,p的任意次方对(p-1)取模后都为1,也就是说bi,j这个根本没有用,理解这个后,写个bfs就可以了,代码如下:
#include <iostream>
#include <queue>
#include <tuple>
#include <string.h>
using namespace std;
const int N = 15, M = 1e4+10;
const int dx[4] = {0, 0, 1, -1};
const int dy[4] = {1, -1, 0, 0};
int a[N][N];
int n, m, p;
int steps[N][N][M];
int bfs()
{
queue<tuple<int, int, int, int>> q;
q.push({0, 0, a[0][0]%(p-1), 0});
steps[0][0][a[0][0]] = 0;
while(!q.empty())
{
auto [x, y, c, step] = q.front();
q.pop();
if(x == n-1 && y == m-1 && c == 0)
{
return step;
}
int nx, ny, nc;
for(int i = 0; i < 4; i++)
{
nx = x + dx[i], ny = y + dy[i];
if(nx < 0 || nx >= n || ny < 0 || ny >= m) continue;
nc = (c + a[nx][ny])%(p-1);
//防止重复的搜某个状态
if(steps[nx][ny][nc] == -1 || steps[nx][ny][nc] > step + 1)
{
q.push({nx, ny, nc, step+1});
steps[nx][ny][nc] = step+1;
}
}
}
return -1;
}
int main()
{
cin >> n >> m >> p;
for(int i = 0; i < n; i++)
for(int j = 0; j < m; j++)
cin >> a[i][j];
int x;
for(int i = 0; i < n; i++)
for(int j = 0; j < m; j++)
cin >>x;
memset(steps, -1, sizeof steps);
cout << bfs() << endl;
return 0;
}E.前缀和前缀最大值
分析:首先求一下序列a的前缀和,假设照度为len,然后 0<= i <= len,分别求出它的前i个数的最大值,然后A类价值就是这些最大值的个数,B类价值就是序列a的所有排列中A类价值的种类数;
可以先求出A类价值的上界和下届,然后B类价值就是上界减下届加一(因为在上界和下届中的A类价值的种类数都是可以取到的),上界就是区间中所有正数的数量,下届就是所有负数在前,正数从小到大排列,得到的相应最大值的种类数
至于为什么是这样,首先决定A类价值的是序列a中前缀和最大值的种类,一个正数一定会使当前的前缀和比前一个的前缀和大,即最大前缀和种类数加一,而一个负数一定会使当前的前缀和比原来小,不会是最大前缀和种类加一,所以上界就是所有正数排在前边的时候,即正数的种类数;而下界的话,之所以是所有负数在前,因为这样会使当前的前缀和越来越小,从而尽可能的让遇见正数后不会使最大前缀种类数增加(如图),并且要使尽可能多的正数被消耗掉,那就是正数在负数后从小到大排列。

又因为种类数是上界减去下届加一,即那就是下界中被负数抵消掉的那部分正数的数量,然后我们发现bi的取值范围很小只有100,所以可以直接记录在1~100范围内相应正数的数量,然后询问时再进行枚举
代码如下:
#include <iostream>
using namespace std;
const int N = 1e5+10;
int a[N];
int fsum[N];//fsum存储负数的前缀和
int sum[N][110];
int main()
{
int n;
cin >> n;
for(int i = 1; i <= n; i++)
{
cin >> a[i];
//求负数的绝对值的前缀和
if(a[i] < 0) fsum[i] = fsum[i-1] - a[i];
else fsum[i] = fsum[i-1];
for(int j = 1; j <= 100; j++)
{
//记录前i个数中正数j出现的次数
sum[i][j] = sum[i-1][j] + (a[i] == j);
}
}
int q;
cin >> q;
int l, r;
while(q--)
{
cin >> l >> r;
int t = fsum[r] - fsum[l-1];
int ans = 0;
for(int i = 1; i <= 100; i++)
{
//求出正数i在l~r中出现的次数
int j = sum[r][i] - sum[l-1][i];
//如果相应的正数对应的总和小于等于区间中负数的总和
if(i*j <= t)
{
t-=i*j;
ans += j;//ans加上相应正数出现的次数
}
else
{
//如果某个正数i的总和大于区间中负数的总和
//ans就加上负数中对应的正数j出现的次数
ans += t/i;
break;
}
}
ans++;//s0也算一种
cout << ans << endl;
}
return 0;
}F.
不会