目录
1.算法运行效果图预览
2.算法运行软件版本
3.部分核心程序
4.算法理论概述
4.1 最小均方误差(MMSE)准则
4.2 量化准则
5.算法完整程序工程
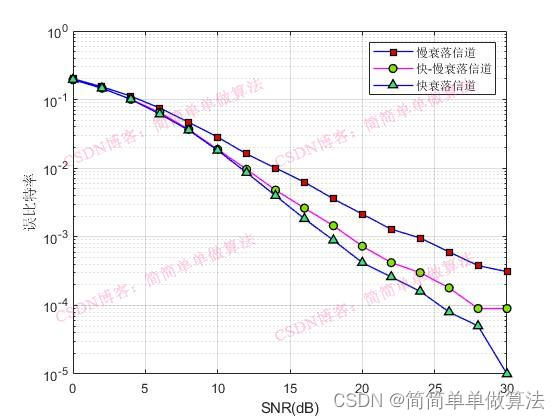
1.算法运行效果图预览
(完整程序运行后无水印)
2.算法运行软件版本
MATLAB2022a
3.部分核心程序
(完整版代码包含详细中文注释)
...................................................................
G = pinv(((h*Pcbk)')*(h*Pcbk)+sigma.^2*eye(length(Pcbk(1,:))))*((h*Pcbk)');
rx = G*rx;
Rdat = [Rdat;rx];
% 寻找最优码字
Vmin = inf;
Num_cbk2 = 1;
% SVD分解和最优预编码矩阵计算
[u,s,v] = svd(h);
for k_book=1:N_bk
% 获取第K个码字
Cbks = func_CB_HH(k_book);
% 根据准则计算MSE
if ij == 1% MMSE准则
Vmse = trace(pinv((Pcbk'*h'*h*Pcbk)/(sigma.^2)+eye(length(Pcbk(1,:)))));
end
if ij == 2% 量化
Vmse = acos(abs(det(v(:,1:2)'*Cbks)));
end
if Vmse < Vmin% 更新最优码字
Num_cbk2 = k_book;
Vmin = Vmse;
end
figure
semilogy(SNRmax,error2(1,:),'-bs',...
'LineWidth',1,...
'MarkerSize',6,...
'MarkerEdgeColor','k',...
'MarkerFaceColor',[0.9,0.0,0.0]);
hold on
semilogy(SNRmax,error2(2,:),'-b^',...
'LineWidth',1,...
'MarkerSize',6,...
'MarkerEdgeColor','k',...
'MarkerFaceColor',[0.2,0.9,0.5]);
grid on
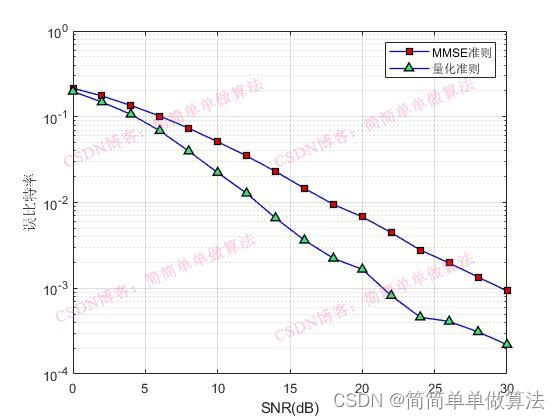
legend('MMSE准则','量化准则');
xlabel('SNR(dB)');
ylabel('误比特率');
153
4.算法理论概述
在现代通信系统中,多天线多输出(Multiple-Input Multiple-Output, MIMO)技术因其能显著提高信道容量和传输可靠性而受到广泛关注。预编码(Precoding)作为一种重要的信号处理技术,在MIMO系统中扮演着核心角色,旨在通过在发射端对信号进行处理,以优化接收端的信号质量。预编码设计涉及到多种准则,其中最小均方误差(Minimum Mean Square Error, MMSE)准则和量化准则(Quantization-based Criteria)是最常见的两种。
4.1 最小均方误差(MMSE)准则

4.2 量化准则
量化准则通常与空间调制或矢量量化技术相结合,侧重于将连续的信号空间映射到一个离散的、易于实现的信号集合中,以适应实际传输的限制。这一准则的核心思想是在信号空间中寻找一组最接近信道特性的信号点集,从而在有限的符号集中最大化传输效率。
在量化预编码中,一个常见方法是格雷码量化(或称为格雷映射),它首先将连续的信号空间分割成多个区域,然后将每个区域中心映射到一个离散的符号点上。如果考虑信道矩阵H和功率约束,量化预编码的目标可以形式化为:

MMSE准则强调的是信号估计的精确度,通过利用CSI来优化预编码矩阵,从而在理论上能够达到最优的接收端信号质量。其优势在于能够有效抑制干扰和噪声,提高系统容量和可靠性,但计算复杂度相对较高,特别是对于大规模MIMO系统,由于矩阵求逆操作的存在,实时实现可能面临挑战。
量化准则则更多地关注信号的实际传输可行性,通过信号空间的离散化处理,使信号适应有限精度的传输媒介。这种方法简化了硬件实现,降低了复杂度,特别适合于对功耗和成本敏感的应用场景。然而,量化操作不可避免地引入量化误差,牺牲了一定的信号质量。
5.算法完整程序工程
OOOOO
OOO
O