前言
在我们的生活中有很多东西都是有大小的,那么该如何去排序?假设有10个数字要你去排序,眼睛一扫就看出来了,那100、1000、10000····要怎么去排?下面就为大家介绍各种排序的算法。
内容
1.冒泡排序
2.选择排序
3.插入排序
4.希尔排序
5.快排
6.归并排序
7.计数排序
1.冒泡排序
冒泡排序排序是一种交换排序,第一个数与第二个数进行比较(这里排序都默认是升序)如果第二个数小于第一个数,那就交换这两数位置然后第二个数再和第三个数依次进行比较,最后会将这个数组中最大数移动到数组最后的位置。
图解
代码
//冒泡排序
void BubbleSort(int* a, int n)
{
for (int i = 0; i < n; i++)
{
//j<n-i这样写是因为每比遍历一次数组就将最大的数放到了数组的最后面
//下次排序就不用再比较了可以提高效率
int flang = 1;//假设已经这个数组已经有序了
for (int j = 0; j < n - i; j++)
{
if (j + 1<n && a[j + 1] < a[j])//j + 1 < n是为防止越界
{
flang = 0;//进入到这里说明数组还没有完全有序
Wsap(&a[j + 1], &a[j]);
}
}
//如果flang==1那就说明这个数组已经有序就可以直接终止循环提高效率
//防止出现 9 1 2 3 4 5 6 7 8 这种情况可以提升代码的效率
if (flang == 1)
{
break;
}
}
}2.选择排序
图解

代码
// 选择排序
void SelectSort(int* a, int n)
{
int min = 0;
for (int j = 0; j < n; j++)
{
min = j;
for (int i = j; i < n; i++)
{
if (a[i] < a[min])
{
min = i;
}
}
Wsap(&a[j], &a[min]);
}
}
//优化算法
void SelectSortpro(int* a, int n)
{
int min = 0,max = 0;
//用begin和end来控制数组的左右两边
int begin = 0, end = n - 1;
while (begin < end)
{
for (int i = begin; i <= end; i++)
{
if (a[i] < a[min])
{
min = i;
}
if (a[i] > a[max])
{
max = i;
}
}
Wsap(&a[begin], &a[min]);
if (a[min] > a[max])
{
max = min;
}
Wsap(&a[end], &a[max]);
//每次遍历之后因为已经将此次遍历的最小和最大放到了两边所以需要缩小区间
begin++;
end--;
}
}3.插入排序
首先要将数组分为已排序和未排序两个部分,一般需要从第二个元素开始因为第一个元素只有一个已经有序了。
图解

代码
// 插入排序
void InsertSort(int* a, int n)
{
for (int i = 0; i < n-1; i++)
{
int begin = 0, end = i;
int key = a[end + 1];
while (end >= begin)
{
if (key < a[end])
{
a[end + 1] = a[end];
end--;
}
//当a[end]>key时就停止循环这时end+1的位置是要插入key的位置
else
{
break;
}
}
//当数组的首元素位置是要插入key的时候end=-1所以end需要加一才是首元素的位置
a[end + 1] = key;
}
}4.希尔排序
图解
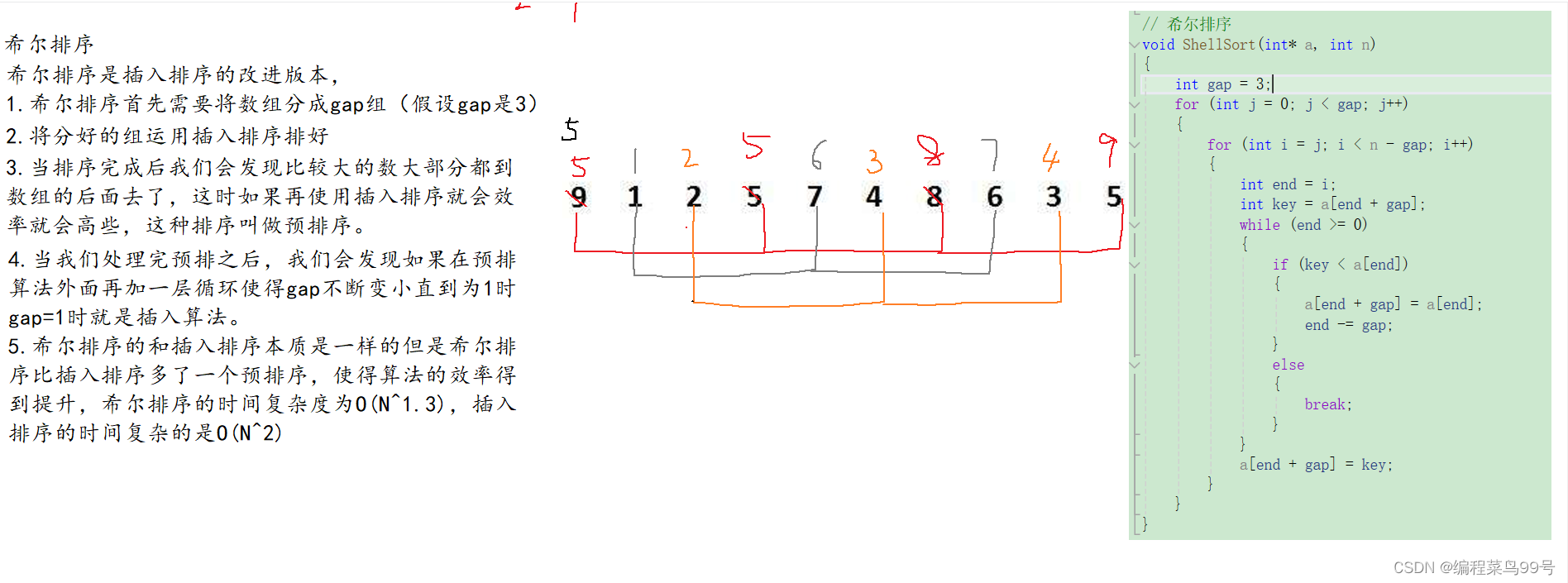
代码
// 希尔排序
void ShellSort(int* a, int n)
{
int gap = n;
//当需要排序的内容过多时不再3组3组的分,需要数组长度不断除3来提升效率
//除完加一是保证最后gap除3之后为零时gap= 1
while (gap > 1)
{
gap = gap/3+1;
for (int i = 0; i < n - gap; i++)//i<n-gap 是保证数组不会越界
{
int end = i;
int key = a[end + gap];
while (end >= 0)
{
if (key < a[end])
{
a[end + gap] = a[end];
end -= gap;
}
else
{
break;
}
}
a[end + gap] = key;
}
}
}5.快排
快排需要借助递归来实现快排的版本有很多图解中为大家一一叙述,快排的非递归需要借助栈来是实现这里就不过多的叙述了详细的思想见图解。
霍尔版本
霍尔版本的快排,需要选择数组最左边的值做为key然后定义一个left和right分别指向最左边和最右边的元素然后right先走遍历数组找到比key小的数停止,left遍历找到比key大的停止然后left和right交换一直到left遇到right或者right遇到left停止,然后交换left或right和key的位置。由key分割数组的区间进行,递归操作。
图解

代码
//霍尔版本
int QuickSort1(int* a, int begin, int end)
{
int key = a[begin], left = begin, right = end, key1 = begin;
while (left < right)
{
while (left < right && a[right] > key)//找比key小的数
{
right--;
}
while (left < right && a[left] <= key)//找比key大的数
{
left++;
}
Wsap(&a[left], &a[right]);
}
Wsap(&a[left], &a[key1]);
return left;
}
//快排
void QuickSort(int* a, int begin, int end)
{
if (begin >= end)
{
return;
}
int key = QuickSort1(a, begin, end);
QuickSort(a, begin, key - 1);
QuickSort(a, key+1, end);
}
双指针法
双指针法的也需要定义一个key指向数组最左边的值,再定义一个prev和cur,prev指向首元素的位置,cur的指向prev的下一个元素。 比较key和cur位置的值如果cur下于key那么就交换prev和cur位置的值如果cur大于key那么cur就加加,直到cur=right就结束。
代码
//双指针法
int QuickSort2(int* a, int left, int right)
{
int prev = left, cur = left + 1, key = left;
while (cur <= right)
{
//++prev != cur 是为了防止prev和cur相等时交换可以提升效率
if (a[cur] < a[key] && ++prev != cur)
{
Wsap(&a[cur], &a[prev]);
}
else
{
cur++;
}
}
Wsap(&a[key], &a[prev]);
return prev;
}
void QuickSort(int* a, int begin, int end)
{
if (begin >= end)
{
return;
}
int key = QuickSort1(a, begin, end);
QuickSort(a, begin, key - 1);
QuickSort(a, key+1, end);
}挖坑法
首先定义key存储首元素,将首元素的位置看做一个坑定义变量ken,再定义一个begin,和end用来遍历数组,end先遍历找到比key小的元素就停止,然后让ken的位置等于end指向的元素再使end位置成为一个新的坑也就是使ken=end。然后begin开始遍历找比key大的数找到后停止再使ken的位置等于begin位置所指向的元素再使begin位置成为新的坑。直到begin和end相遇然后让begin和end指向的位置等于key。
代码
//挖坑法
int QuickSort3(int* a, int left, int right)
{
int ken = left, key = a[left], begin = left, end = right;
while (begin < end)
{
while (a[end] >= key&& begin < end)
{
end--;
}
a[ken] = a[end];
ken = end;
while (a[begin] <= key&& begin < end)
{
begin++;
}
a[ken] = a[begin];
ken = begin;
}
a[begin] = key;
return begin;
}
//快排
void QuickSort(int* a, int begin, int end)
{
if (begin >= end)
{
return;
}
int key = QuickSort3(a, begin, end);
QuickSort(a, begin, key - 1);
QuickSort(a, key+1, end);
}快排的优化
三数取中和小区间优化

代码
//三数取中
int GetMid(int left, int mid, int end)
{
if (left > mid)
{
if (end > left)//end>left>mid
{
return left;
}
else if (mid > end)
{
return mid;
}
else
{
return end;
}
}
else//mid>left
{
if (end > mid)//end>mid>left
{
return mid;
}
else if (left > end)//mid>left>end
{
return left;
}
else
{
return end;
}
}
}
//快排
void QuickSort(int* a, int begin, int end)
{
if (begin >= end)
{
return;
}
if (end - begin + 1 <= 10)
{
InsertSort(a, end - begin + 1);
}
else
{
int key = QuickSort3(a, begin, end);
QuickSort(a, begin, key - 1);
QuickSort(a, key + 1, end);
}
}6.归并排序
递归版本
归并的本质是分组,将数组分成两份一份是有序的另一份也是有序的,然后创建数组tmp从两份有序的数首元素开始遍历谁小谁就尾插到tmp数组中,直到两份数组都没有元素。将tmp数组中的内容拷贝到原数组中。

代码
//归并排序
void _MergeSort(int* a, int* tmp, int left, int right)
{
if (left == right)
{
return;
}
int mid = (right + left) / 2;
_MergeSort(a, tmp, left, mid);
_MergeSort(a, tmp, mid+1, right);
int begin1 = left, begin2 = mid+1, end1 = mid, end2 = right;
int j = 0;
while (begin1 <= end1 && begin2 <= end2)
{
//谁小谁就尾插到tmp中
if (a[begin1] <= a[begin2])
{
tmp[j++] = a[begin1++];
}
else
{
tmp[j++] = a[begin2++];
}
}
//当出现6 7 8 9,2 3 4 5时6大于第二份中的所有数时
//我们需要将第一份剩余是数组继续插入到tmp中
while (begin1 <= end1)
{
tmp[j++] = a[begin1++];
}
while (begin2 <= end2)
{
tmp[j++] = a[begin2++];
}
//每次递归都要拷贝一次因为本质是对a中的数据排序但是现在我们是在tmp使其有序
//所以每次排序完都要拷贝回去使a中也有序
memcpy(a+left, tmp, (right - left + 1)*sizeof(int));
}
//归并排序
void MergeSort(int* a, int n)
{
//创建数组tmp
int* tmp = malloc(sizeof(int) * n+1);
if (tmp == NULL)
{
perror("tmp fail:");
return;
}
_MergeSort(a, tmp, 0, n);
}非递归版本
当递归的层度太深的话就会导致栈溢出的分险,所以我们需要尝试不借用递归实现归并排序。归并的本质是对数组进行分组比较,最开始的时候是每组有一个元素然后每相邻的两个组进行比较。1X1归并2X2归并4X4归并直到数组有序(当然也会出现不能均匀分割的情况,但是3X4依旧可以归并)。归并的难点在于怎么样去控制下标进行分组,首先对数组进行1X1的分组定义变量gap=1(gap组),进行遍历数组相邻的两组进行比较,小的就尾插到copy数组中,然后再将已经有序的部分拷贝会原数组中这是一次循环,在这个循坏外再加上一次循环用来控制每组元素的个数直到整个数组有序。
代码
//归并非递归
void MergeSortNOT(int* a, int n)
{
//创建coap数组用于拷贝
int* copy = (int*)malloc(sizeof(int)*(n+1));
if (copy==NULL)
{
perror("copy fail:");
return;
}
int gap = 1;//组数
while (gap < n)
{
for (int i = 0; i < n; i += 2 * gap)
{
//定义变量分割区间
int begin1 = i, end1 = i + gap - 1,
begin2 = i + gap, end2 = i + 2 * gap - 1;
//printf("[%d %d] [%d %d]", begin1, end1, begin2, end2);
//防止越界情况的发生
if (end1 > n)
{
break;
}
if (end2 > n)
{
end2 = n - 1;
}
int j = 0;
while (begin1 <= end1 && begin2 <= end2)
{
//谁小谁就尾插到tmp中
if (a[begin1] <= a[begin2])
{
copy[j++] = a[begin1++];
}
else
{
copy[j++] = a[begin2++];
}
}
while (begin1 <= end1)
{
copy[j++] = a[begin1++];
}
while (begin2 <= end2)
{
copy[j++] = a[begin2++];
}
memcpy(a+i, copy, (end2-i+1) * sizeof(int));
}
gap*=2;
printf("\n");
}
}7.计数排序
计数排序是创建一个数组count用来记录a数组中元素的出现的个数,然后通过数组下标的自然有序使a数组中的元素出现在正确的位置上,使a有序。
代码
//计数有序
void CountSort(int* a, int n)
{
//首先找出数组中的最大,最小值
int max = a[0], min = a[0];
for (int i = 0; i < n; i++)
{
if (a[i] > max)
max = a[i];
if (a[i] < min)
min = a[i];
}
//创建max-min+1个空间是为防止出现6 6 6 6 10的情况减少申请的内存空间
int* count = calloc((max-min+1),sizeof(int));
if(count==NULL)
{
perror("count fail::");
}
for (int i = 0; i < n; i++)
{
count[a[i] - min]++;
}
int b = 0;
for (int j = 0; j < (max-min+1); j++)
{
while (count[j]--)
{
a[b++] = j + min;
}
}
free(count);
}总结
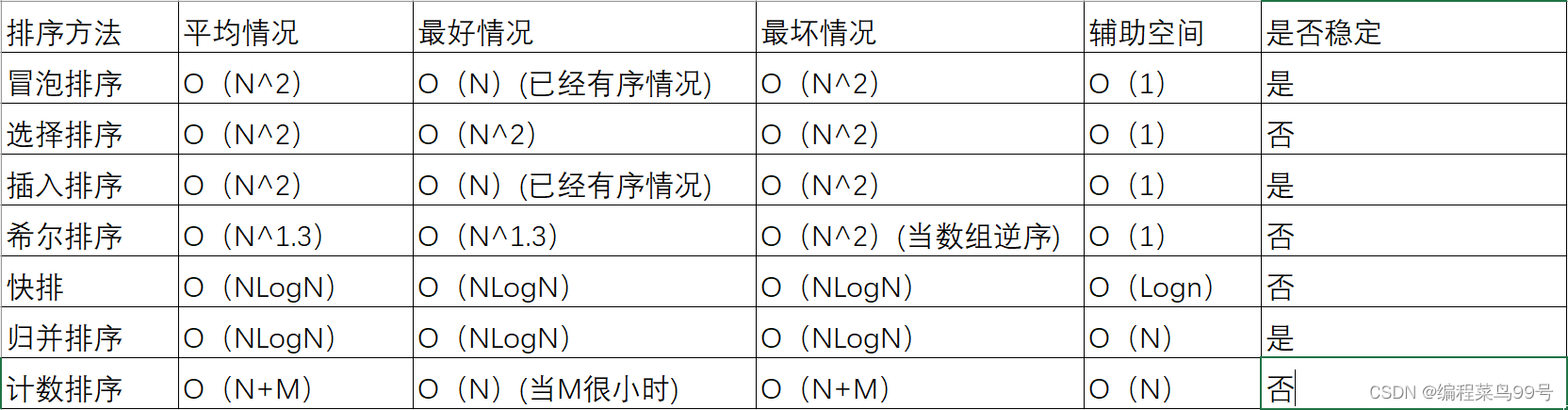
本篇章讲述了大部分的常用的排序,还有一个堆排将在二叉树中详细讲解。
希望大大多多指点。
记得三连哦!感谢!感谢!感谢!