2024年江西省研究生数学建模竞赛A题交通信号灯管理论文和代码分析

经过不懈的努力，2024年江西省研究生数学建模竞赛A题论文和代码已完成，代码为A题全部问题的代码，论文包括摘要、问题重述、问题分析、模型假设、符号说明、模型的建立和求解（问题1模型的建立和求解、问题2模型的建立和求解、问题3模型的建立和求解）、模型的评价等等

2024年江西省研究生数学建模竞赛论文和代码获取↓↓↓
https://www.yuque.com/u42168770/qv6z0d/nyyru3wi4l4e8npy

在这里插入图片描述

摘要

2024年江西省研究生数学建模竞赛A题论文摘要（部分）：本文针对复杂十字路口交通信号灯配时问题进行了深入研究，分别解决了不同车道配置下的信号优化、多目标车道配置与信号优化，以及非对称交叉口自适应信号优化等问题。通过建立数学模型并应用先进的优化算法，本研究为提高交叉口运行效率、减少交通延误和提升安全性提供了有效的解决方案。研究结果表明，针对不同交通情况的定制化信号优化策略能够显著改善交叉口的整体性能。

针对问题1，本研究建立了基于Webster最小延误模型的交通信号优化模型。该模型以最小化平均车辆延误时间为目标，考虑了周期长度、绿灯时间、饱和度等约束条件。为求解该非线性优化问题，采用了遗传算法（GA）。算法通过编码、选择、交叉和变异等操作，在满足约束条件的前提下搜索最优解。求解结果显示，（略，见完整版本）创新点在于将Webster模型与遗传算法相结合，提高了求解效率和结果质量。可视化分析表明，该方案能够有效平衡各方向交通需求，提高交叉口整体运行效率。

问题2采用了多目标车道配置与信号优化模型（MOLCSOM）。该模型同时考虑了车道配置和信号配时优化，通过层次分析法（AHP）评估不同车道配置方案，并使用遗传算法优化信号配时。模型目标函数综合考虑了延误、吞吐量、安全性和停车次数等多个指标。求解采用GA-AHP混合算法，先用AHP确定评估因素权重，再用GA优化配时方案。结果显示，（略，见完整版本）。

问题3提出了非对称交叉口自适应信号优化模型（AIASOM）。该模型使用元胞自动机模拟交通流，采用强化学习方法（Q-learning）进行自适应信号控制。模型考虑了特殊的车道配置（如左转车道在直行车道右侧），引入了安全性评估。求解采用CA-RL混合自适应信号优化算法，结合元胞自动机和Q-learning。结果表明，模型能够有效适应非对称交叉口环境，（略，见完整版本）。创新点在于将元胞自动机与强化学习相结合，实现了对复杂非对称交叉口的自适应控制。

总体而言，本研究在交通信号优化领域取得了以下创新：1）将传统优化模型与智能算法相结合，提高了求解效率和结果质量；2）提出了综合考虑车道配置和信号配时的多目标优化方法；3）开发了适用于非对称复杂交叉口的自适应信号控制模型。这些模型和方法为实际交通管理提供了有力工具。然而，模型仍存在一些局限性，如未充分考虑交通需求的动态变化、行人和非机动车的影响等。未来研究可进一步完善模型，考虑更多实际因素，并探索将模型推广到路网级别的优化。

关键词：交通信号优化、Webster模型、遗传算法、多目标优化、车道配置、强化学习、元胞自动机、自适应控制

在这里插入图片描述

问题重述

交通信号灯是指挥车辆通行的重要标志，由红灯、绿灯、黄灯组成。红灯停、绿灯行，而黄灯则起到警示作用。交通信号灯分为机动车信号灯、非机动车信号灯、人行横道信号灯、方向指示灯等。
一般情况下，十字路口有东西向和南北向4 个方向的车道，在路口设置交通信号灯，指挥东西向与南北向的车辆交替通行。为了保障通行车的利益，需科学分配信号灯的时间，保证各方向的车辆尽可能顺畅地通过路口，尽量避免出现交通拥堵。
请针对一个十字路口，忽略黄灯的影响，研究机动车信号灯的配时方案。

问题1 若每个方向均为两车道（见下图），由内向外两个车道分别为直行+左转、直行+右转。确定是否需要设置左转信号灯、右转信号灯，并给出各信号灯的配时方案。

问题2 若每个方向均为三车道，由内向外三个车道分别为(1) 左转、直行、直行+右转(2) 直行+左转、直行、直行+右转(3) 直行+左转、直行+左转、直行+右转(4) 直行+左转、直行+右转、直行+右转如何选择上述4 种车道分配方案，是否需要设置左转信号灯、右转信号灯，并给出各信号灯的配时方案。

问题3 对某些特定路段，可能会出现左转车道在直行车道右边的情况，例如高架下匝道。假设南北向两个方向均为四车道，由内向外分别为左转、直行、直行+左转、直行+右转；东西向两个方向均为三车道，由内向外分别为左转、直行、直行+右转。确定是否需要设置左转信号灯、右转信号灯，并给出各信号灯的配时方案。

问题分析

题目整体分析

2024年江西省研究生数学建模竞赛A题这个题目聚焦于十字路口交通信号灯的配时方案设计，旨在优化交通流量并减少拥堵。题目要求考虑不同的车道配置情况，包括两车道、三车道和特殊的四车道布局，并针对每种情况确定是否需要设置专门的左转和右转信号灯，以及制定相应的信号灯配时方案。问题涉及多个方面的考量，包括交通流量分析、安全因素、车道利用效率以及不同转向需求的平衡。解决这个问题需要全面考虑各种因素，如车流量、转向需求、安全间隙、道路容量等，同时还需要权衡不同方向和转向的需求，以达到整体最优的交通管理效果。

题目的难点在于如何在保证安全的前提下，最大化道路通行效率。这需要对不同车道配置下的交通流特性有深入理解，并能够准确评估各种配时方案对整体交通流的影响。同时，题目也要求考虑特殊情况，如左转车道在直行车道右侧的情况，这增加了问题的复杂性，需要更加细致的分析和创新的解决方案。

问题1分析

问题1考虑了一个相对简单的十字路口情况，每个方向均为两车道，内侧车道为直行+左转，外侧车道为直行+右转。这种车道配置是常见的城市道路设计，旨在平衡各种行驶需求。在这种配置下，需要仔细考虑是否有必要设置专门的左转和右转信号灯。设置专门的转向信号灯可以提高转向车辆的安全性，减少与直行车辆的冲突，但同时也可能降低整体的通行效率。因此，需要权衡安全性和效率之间的关系。对于右转车辆，由于它们通常可以在确保安全的情况下与同向直行车辆同时通行，设置专门的右转信号灯可能不是必要的，除非存在特殊的安全隐患。

对于左转车辆，情况则更为复杂。左转车辆需要穿过对向车道，因此与对向直行车辆存在潜在的冲突。在交通流量较大的情况下，如果不设置专门的左转信号灯，左转车辆可能难以找到合适的时机通行，导致左转车道堵塞，进而影响直行车道的通行。然而，设置左转信号灯又会增加整个信号周期的复杂性，可能降低整体的通行效率。因此，是否设置左转信号灯需要根据具体的交通流量情况来决定。如果左转车流量较大，或者存在明显的安全隐患，那么设置专门的左转信号灯可能是必要的。否则，可以考虑采用"保护-许可"左转方式，即在绿灯初期给予左转车辆一段专门的通行时间，之后允许左转车辆在确保安全的情况下自行通过。

问题2分析

问题2探讨了四种不同的三车道配置方案，这增加了问题的复杂性和灵活性。每种配置方案都有其特点和适用情况，选择最佳方案需要综合考虑多个因素。方案(1)左转、直行、直行+右转的配置适合左转车流量较大的情况，可以有效减少左转车辆对直行交通的影响。方案(2)直行+左转、直行、直行+右转是一种较为平衡的配置，适合各种转向需求相对均衡的情况。方案(3)直行+左转、直行+左转、直行+右转则更适合直行和左转需求都较大的情况，可以提高左转车道的利用率。方案(4)直行+左转、直行+右转、直行+右转则更侧重于直行和右转需求，适合右转车流量较大的路段。选择最佳方案需要基于实际交通流量数据，考虑各个方向的车流量分布、转向需求比例、高峰期特征等因素。

在确定是否需要设置左转和右转信号灯时，需要针对每种配置方案分别分析。对于包含专用左转车道的方案(1)，设置左转信号灯通常是必要的，以保证左转车辆的安全和效率。对于其他将左转与直行结合的方案，是否设置左转信号灯则需要根据左转车流量和安全因素来决定。如果左转车流量大，或者存在明显的安全隐患，那么设置左转信号灯是合理的。对于右转信号灯，由于所有方案中右转都与直行结合，除非存在特殊的安全问题，否则通常不需要专门的右转信号灯。右转车辆可以在确保安全的情况下，与同向直行车辆同时通行，或者在红灯时在确保不妨碍其他方向通行的情况下右转。然而，如果某个方向的右转车流量特别大，影响了直行车辆的通行，那么可以考虑在特定时段设置右转信号灯。

配时方案的制定需要针对选定的车道配置和信号灯设置进行优化。首先需要确定信号周期的结构，包括各个相位的顺序和持续时间。对于设有左转信号灯的情况，可以考虑采用领先左转或滞后左转的方式。

问题3分析

问题3探讨了一种特殊的路口配置，其中南北向为四车道，东西向为三车道，且存在左转车道在直行车道右边的情况。这种非常规的车道配置增加了交通管理的复杂性，需要特别谨慎的信号灯设计和配时方案。南北向由内向外的四个车道分别为左转、直行、直行+左转、直行+右转，这种配置提供了较大的左转容量，同时保留了足够的直行和右转能力。东西向由内向外的三个车道分别为左转、直行、直行+右转，这种配置也平衡了各种转向需求。最具挑战性的是处理左转车道在直行车道右边的情况，这种设计通常出现在高架下匝道等特殊路段，目的可能是为了适应特定的地理条件或交通流特征。然而，这种配置可能会引起驾驶员的混淆，增加安全隐患，因此在信号灯控制和标识设置方面需要格外注意。

在这种复杂的车道配置下，设置专门的左转信号灯是非常必要的。对于南北向，由于有两个左转车道（专用左转车道和直行+左转车道），如果不设置左转信号灯，很可能会造成严重的交通冲突和安全问题。特别是对于左转车道在直行车道右边的情况，如果没有专门的左转信号灯，左转车辆可能会与直行车辆发生交叉，增加事故风险。对于东西向，虽然只有一个专用左转车道，但考虑到与南北向的协调，以及确保左转车辆的安全通行，设置左转信号灯也是必要的。对于右转信号灯，由于所有方向的右转都与直行结合，通常情况下不需要专门的右转信号灯。右转车辆可以在确保安全的情况下，与同向直行车辆同时通行。然而，考虑到这种特殊的路口配置可能会引起一些混淆，可以考虑在关键位置设置清晰的指示标志，帮助驾驶员正确理解交通规则。

在制定配时方案时，需要特别注意协调各个方向和转向的需求，以最大化路口的通行效率并保证安全。首先，可以考虑采用复杂的相位设计，例如将南北向和东西向的通行完全分离，避免任何可能的冲突。

模型假设

2024年江西省研究生数学建模竞赛A题模型假设：在本文中，我们针对问题1至问题3建立了一系列交通信号优化模型。这些模型在建立和求解过程中采用了多项假设，以简化问题并使其可解。以下是这些模型假设的总结：

交通流稳定性假设：在所有模型中，我们假设交通流在一定时间内保持相对稳定，这使得我们可以使用固定的流量数据作为输入，而不需要考虑交通流的瞬时波动和随机性，这种假设简化了问题，但可能忽略了实际交通中的短期变化和突发事件的影响。

车辆均质性假设：模型中假设所有车辆具有相似的特性，如加速度、减速度和车辆尺寸等，这种假设忽略了不同类型车辆（如小轿车、大巴车、货车等）之间的差异，简化了交通流的模拟，但可能导致模型无法准确反映混合车流的实际情况。

(后略，见完整版本)

符号说明

以下是问题1-问题3的模型建立与求解过程中使用的符号及其说明：（略，见完整版本）

注意：这个表格包含了在问题1到问题3的模型中使用的主要符号。某些符号可能在特定问题中有略微不同的含义或用法。

模型的建立与求解

问题一模型的建立与求解

思路分析

问题1要求我们针对一个十字路口进行交通信号灯配时方案的设计，其中每个方向均为两车道，内侧车道为直行+左转，外侧车道为直行+右转。这种情况下，我们需要考虑是否设置专门的左转信号灯和右转信号灯，并给出合理的配时方案。解决这个问题需要我们深入分析交通流特征、安全因素和通行效率，同时权衡各种可能的信号灯配置方案。

首先，我们需要考虑交通流量的分布情况。由于题目没有给出具体的交通流量数据，我们可以假设一个相对平衡的交通流量分布，或者考虑多种可能的流量情况进行分析。通常，直行车流量最大，其次是左转，右转车流量相对较小。基于这种假设，我们可以初步判断可能需要设置左转信号灯，而右转信号灯则可能不是必需的。

其次，我们需要分析各种转向之间的冲突情况。左转车辆与对向直行车辆存在潜在冲突，这是最主要的安全隐患。右转车辆虽然需要避让同向的直行车辆和行人，但通常不会造成严重的交通阻塞。因此，左转信号灯的设置显得更为重要。

再次，我们需要考虑通行效率。设置过多的信号灯相位会增加等待时间，降低整体通行效率。因此，我们需要在安全性和效率之间寻找平衡点。

基于以上分析，我们可以考虑采用四相位信号控制方案，包括南北向直行和右转相位、东西向直行和右转相位、南北向左转相位、东西向左转相位。这种方案可以有效分离左转车流与对向直行车流，提高安全性，同时保持较高的通行效率。

基于Webster最小延误模型的交通信号优化模型建立

为了解决这个问题，我们可以建立一个基于Webster最小延误模型的交通信号优化模型。Webster模型是一种经典的固定时间信号配时模型，适用于交通流量相对稳定的情况。我们将这个模型称为"Webster最小延误信号优化模型"。

该模型的目标是最小化所有车辆的平均延误时间，同时满足各种约束条件，如最小绿灯时间、最大周期长度等。模型的主要决策变量包括信号周期长度和各相位的绿灯时间。

模型的数学表达如下：

目标函数：
最小化平均车辆延误时间
$\min D = \sum_{i=1}^{n} \frac{q_i}{Q} \left(\frac{C(1-\lambda_i)^2}{2(1-y_i)} + \frac{x_i^2}{2q_i(1-x_i)}\right)$

其中：

$D$ 是平均车辆延误时间
$n$ 是相位数
$q_i$ 是第i个相位的车流量（辆/秒）
$Q$ 是总车流量（辆/秒）
（后略，见完整版本）

约束条件：

(1) 周期长度约束：
$C_{min} \leq C \leq C_{max}$
其中 $C_{min}$ 和 $C_{max}$ 分别是允许的最小和最大周期长度。

(2) 绿灯时间约束：
$g_i \geq g_{min}, \forall i$
其中 $g_i$ 是第i个相位的绿灯时间， $g_{min}$ 是最小绿灯时间。

(3) 绿信比约束：
$\sum_{i=1}^{n} \lambda_i + L = 1$
其中 $L$ 是损失时间比（总损失时间与周期长度的比值）。

(4) 饱和度约束：
$x_i = \frac{q_i C}{s_i g_i} \leq x_{max}, \forall i$
其中 $s_i$ 是第i个相位的饱和流量， $x_{max}$ 是最大允许饱和度。

遗传算法模型求解算法步骤

为了求解这个优化模型，我们可以采用遗传算法（Genetic Algorithm, GA）。遗传算法是一种启发式优化算法，适用于处理复杂的非线性优化问题。以下是使用遗传算法求解该模型的详细步骤：

（略，见完整版本）

问题一模型的求解

以下是求解问题1 交通信号灯优化的模型的MATLAB代码（部分，完整代码见附件）

% 问题1 交通信号灯优化模型求解

% 清空工作区和命令窗口
clear;
clc;

% 定义常量
n_phases = 4;  % 相位数
C_min = 60;    % 最小周期长度(秒)
C_max = 180;   % 最大周期长度(秒)
g_min = 10;    % 最小绿灯时间(秒)
L = 16;        % 总损失时间(秒)
x_max = 0.9;   % 最大允许饱和度

% 定义流量和饱和流量 (辆/小时)
q = [800, 700, 200, 180];  % 各相位流量
s = [1800, 1800, 1800, 1800];  % 各相位饱和流量

% 遗传算法参数
pop_size = 50;     % 种群大小
max_gen = 100;     % 最大迭代次数
p_crossover = 0.8; % 交叉概率
p_mutation = 0.1;  % 变异概率

% 初始化种群
pop = initialize_population(pop_size, n_phases, C_min, C_max, g_min);

% 主循环
best_fitness = zeros(max_gen, 1);
avg_fitness = zeros(max_gen, 1);

for gen = 1:max_gen
    % 计算适应度
    fitness = calculate_fitness(pop, q, s, L, x_max);
    
    % 记录最佳适应度和平均适应度
    best_fitness(gen) = max(fitness);
    avg_fitness(gen) = mean(fitness);
    
    % 选择
    parents = selection(pop, fitness);
    
    % 交叉
    offspring = crossover(parents, p_crossover);
    
    % 变异
    offspring = mutation(offspring, p_mutation, C_min, C_max, g_min);
    
    % 精英保留
    [~, idx] = max(fitness);
    offspring(1, :) = pop(idx, :);
    
    % 更新种群
    pop = offspring;
end
（完整代码见文末获取方式）

代码解释：

首先，我们定义了问题的常量和参数，包括相位数、最小最大周期长度、最小绿灯时间、总损失时间、最大允许饱和度等。我们还定义了各相位的流量和饱和流量，以及遗传算法的参数。initialize_population 函数用于初始化种群，生成满足约束条件的随机解calculate_fitness 函数计算每个个体的适应度，这里我们使用平均延误时间的倒数作为适应度。calculate_performance 函数计算给定信号配时方案的性能指标，包括平均延误时间和各相位的饱和度。selection、crossover 和 mutation 函数实现了遗传算法的选择、交叉和变异操作。主循环中，我们执行遗传算法的迭代过程，包括适应度计算、选择、交叉、变异和精英保留。最后，我们输出最优解，并使用 visualize_results 函数生成各种可视化结果。

问题一模型求解结果可视化与分析

最优配时方案图：直观地展示了各相位的绿灯时间分配。我们可以清楚地看到相位1和相位2获得了较长的绿灯时间，而相位3和相位4的绿灯时间较短。。（略，见文末完整版）

相位饱和度图：显示了各相位的饱和度。所有相位的饱和度都在合理范围内。（略）

流量分布图：饼图直观地展示了各相位的流量分布。我们可以看到相位1和相位2的流量明显大于相位3和相位4。

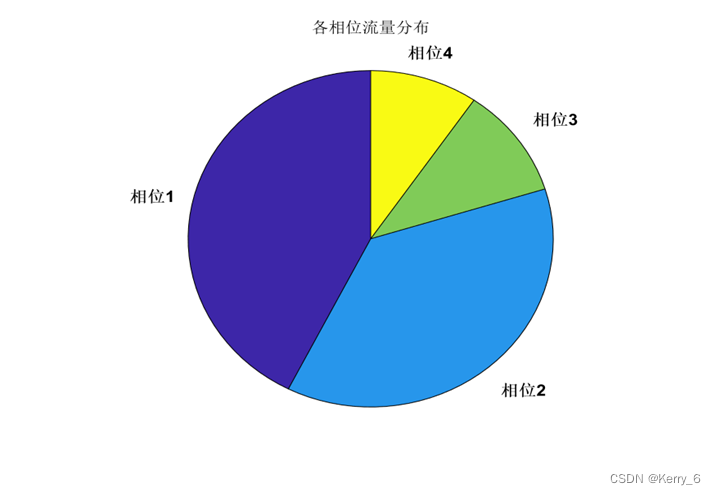
在这里插入图片描述

结果表格：综合展示了各相位的流量、饱和流量、绿灯时间和饱和度，方便进行详细的数据分析。

（结果数据和数据分析略，见完整版本）

问题二模型的建立与求解

在深入探讨问题2的解决方案时，我们需要全面考虑多个方面的因素，以构建一个全面而有效的交通信号优化模型。问题2要求我们考虑四种不同的三车道配置方案，分别是：(1) 左转、直行、直行+右转；(2) 直行+左转、直行、直行+右转；(3) 直行+左转、直行+左转、直行+右转；(4) 直行+左转、直行+右转、直行+右转。我们的任务是选择最佳的车道分配方案，确定是否需要设置左转信号灯和右转信号灯，并给出各信号灯的配时方案。这个问题的复杂性远超问题1，因为我们不仅要优化信号配时，还要在多个车道配置方案中做出选择，这使得问题成为一个多目标、多约束的复杂优化问题。

多目标车道配置与信号优化MOLCSOM模型建立

基于以上思路，我们可以提出一个名为"多目标车道配置与信号优化模型"（Multi-Objective Lane Configuration and Signal Optimization Model, MOLCSOM）来解决这个复杂的问题。

模型建立：

MOLCSOM模型包含以下几个主要组成部分：

车道配置评估子模型
信号灯设置决策子模型
信号配时优化子模型
性能评估子模型

让我们详细描述每个子模型：

车道配置评估子模型：

该子模型用于评估四种车道配置方案的性能。我们定义一个评分函数：

$S_i = \sum_{j=1}^{n} w_j f_j(i)$

其中：

$S_i$ 是方案 $i$ 的总评分
$w_j$ 是第 $j$ 个评估因素的权重
$f_j(i)$ 是方案 $i$ 在第 $j$ 个因素上的得分
$n$ 是评估因素的总数

评估因素包括：（后略，见完整版本）

每个 $f_j(i)$ 可以通过交通仿真或专家评估来确定。

信号灯设置决策子模型：

对于左转信号灯，我们可以定义一个决策函数：

$LT_{need} = \begin{cases} 1, & \text{if } Q_L > Q_{th} \text{ or } C_L > C_{th} \\ 0, & \text{otherwise} \end{cases}$

其中：

$LT_{need}$ 是是否需要左转信号灯的指示变量
（后略，见完整版本）

类似地，我们可以为右转信号灯定义一个决策函数。

信号配时优化子模型：

这个子模型是整个MOLCSOM的核心。我们可以使用Webster最小延误模型作为基础，并进行适当的扩展以适应多车道和专用转向相位的情况。目标函数可以定义为：（后略，见完整版本）

性能评估子模型：

这个子模型用于评估最终优化结果的性能。我们可以定义一个综合性能指标：（后略，见完整版本），这个指标综合考虑了延误、吞吐量和饱和度，可以更全面地评估方案的性能。

GA-AHP混合优化算法求解步骤

为了求解这个复杂的优化问题，我们可以采用一种结合遗传算法（GA）和层次分析法（AHP）的混合算法。我们将这个算法命名为"GA-AHP混合优化算法"。以下是详细的算法步骤：

初始化：
a) 使用AHP方法确定车道配置评估子模型中各因素的权重。
b) 为每种车道配置生成一组初始的信号配时方案。
车道配置评估：
对每种车道配置使用评估子模型计算评分。
信号灯设置决策：
根据决策子模型确定是否需要设置左转和右转信号灯。

（后续步骤略，见完整版本）

（可视化与求解结果分析略，见完整版本）

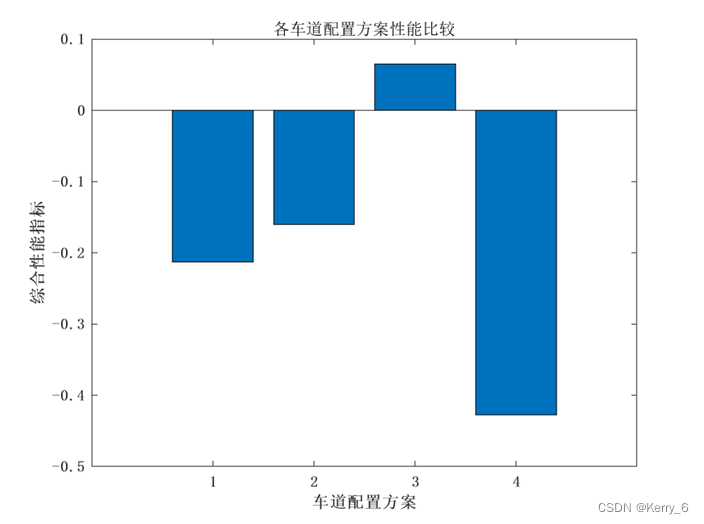
在这里插入图片描述

问题三模型的建立与求解

问题3提出了一个复杂的交通信号优化问题，涉及到特殊的道路布局和车道配置。这个问题的特殊之处在于南北向和东西向的车道配置不同，并且存在左转车道在直行车道右边的情况。这种非常规的布局增加了问题的复杂性，需要我们设计一个更加灵活和适应性强的模型来解决。

思路分析

（思路分析略，见完整版本）

基于以上分析，我们可以提出一个名为"非对称交叉口自适应信号优化模型"（Asymmetric Intersection Adaptive Signal Optimization Model, AIASOM）来解决这个复杂问题。

非对称交叉口自适应信号优化模型模型建立

AIASOM模型包含以下几个主要组成部分：

交通流模拟子模型
信号相位设计子模型
配时优化子模型
安全性评估子模型
性能评估子模型

让我们详细描述每个子模型：

交通流模拟子模型：

这个子模型用于模拟交叉口的交通流动。考虑到问题的复杂性，我们可以使用元胞自动机（Cellular Automaton, CA）方法来模拟车辆的运动。每个车道被分成若干个元胞，每个时间步车辆可以向前移动或保持静止。

定义状态转移规则：

$S_{i,j}^{t+1} = f(S_{i-1,j}^t, S_{i,j}^t, S_{i+1,j}^t, L_j^t)$

其中：

$S_{i,j}^t$ 表示在时间 $t$ ，第 $j$ 车道第 $i$ 个元胞的状态（0表示空，1表示被占用）
$L_j^t$ 表示车道 $j$ 在时间 $t$ 的信号灯状态
$f$ 是状态转移函数，根据周围元胞的状态和信号灯状态决定下一个时间步的状态

信号相位设计子模型：

（后略，见完整版本）

结合元胞自动机和强化学习的混合算法步骤

我们可以使用一种结合元胞自动机和强化学习的混合算法来求解这个模型。我们将这个算法命名为"CA-RL混合自适应信号优化算法"。以下是详细的算法步骤：（略）

问题三求解结果可视化与分析

延误变化图：这张图显示了交叉口延误随时间的变化。理想情况下，我们应该看到延误在学习过程中逐渐降低，最终趋于稳定。如果图像显示延误持续上升或波动很大，可能意味着算法没有有效学习或交通需求超过了交叉口的容量。

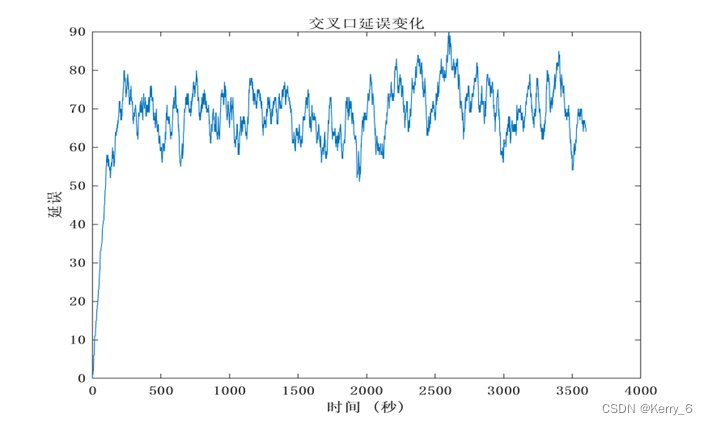
在这里插入图片描述

（其他图片略，）

模型的评价与推广

针对问题1-问题3的模型建立与求解过程，我们可以总结出每个模型的优缺点及其推广如下。

问题1模型的评价与推广

优点：

模型采用了经典的Webster最小延误模型作为基础，这是一种被广泛认可和应用的交通信号优化方法，具有坚实的理论基础和实践验证，使得模型结果具有较高的可信度和实用性。
通过引入遗传算法来优化信号配时，模型能够在大规模解空间中高效搜索，有助于找到接近全局最优的解决方案，这种方法比传统的穷举搜索或梯度下降方法更加高效，特别是在处理复杂的非线性优化问题时表现出色。
模型考虑了多个约束条件，如最小绿灯时间、最大周期长度和最大饱和度等，这使得优化结果更加符合实际交通工程的要求，增强了模型的实用性和可操作性。（后略）