书接上文,我们讲完了哈代温伯格基因型频率,也使用数据进行了拟合,那么接下来就是考虑一些计算的问题:
【基于R语言群体遗传学】-1-哈代温伯格基因型比例-CSDN博客
【基于R语言群体遗传学】-2-模拟基因型(simulating genotypes)-CSDN博客
如果我们有群体样本中个体的基因型,那么我们不需要假设哈代-温伯格比例来从表型频率估计等位基因频率。我们可以简单地计数等位基因。每个杂合子有一个等位基因的拷贝,而纯合子有两个拷贝(再次假设是一个二倍体生物)。由于每个采样的个体在每个位点都有两个拷贝,所以观察到的等位基因总数是采样个体数量的两倍。
然后,我们可以通过将杂合子的数量加上纯合子数量的两倍(因为每个纯合子有两个等位基因的拷贝),然后除以采样个体数量的两倍(因为每个采样的个体携带两个位点),来计算特定等位基因的频率:
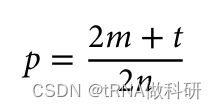
哈代温伯格假设
为了得到p² + 2pq + q²并运行这里用来说明期望的模拟,我们做了以下假设:
• 被考虑的有机体是二倍体。
• 被考虑的有机体仅通过性繁殖(无克隆)。
• 不存在具有不同等位基因频率的独立种群,无论它们之间是否有迁移。
• 我们所考虑的种群在大小上是无限大的。
• 所有交配都是随机发生的。
• 没有遗传变异受到自然选择的影响(等位基因的生存和繁殖差异)。
• 没有遗传变异因突变而丢失或获得(没有等位基因突变为新的等位基因)。
• 世代之间不重叠。一旦繁殖发生,所有的亲本消失,只有产生的后代贡献给下一代。
显然,这些期望在生物学上并不非常现实。然而,哈代-温伯格期望对大多数这些假设的违反都相当稳健,除了前三个:单倍体或多倍体有机体必须以不同但合理的方式处理,通过无性繁殖的有机体可能与哈代-温伯格期望有很大偏差,种群细分可能导致显著偏差。
简单的疾病例子
观察到三种隐性疾病表型的携带者(杂合子)和受影响个体(纯合子)的数量:囊性纤维化(CF)、镰状细胞贫血(SC)和β-地中海贫血(βT)。数据改编自Lazarin等人2013年的研究。
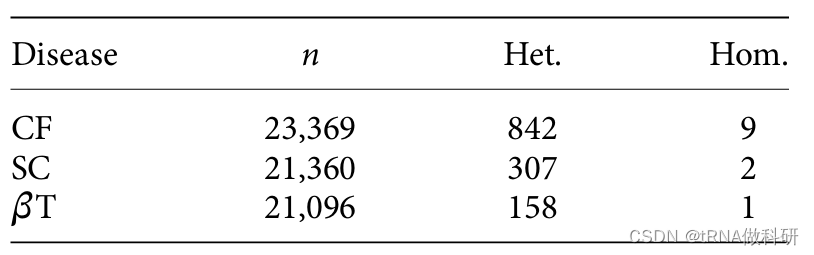
我们首先看看筛查中囊性纤维化(CF)纯合子的个体数量:这个数字(9)表明这九个个体总共携带了十八个CF等位基因。现在,携带者(杂合子)的数量相当多(842),对于一个罕见等位基因来说,这可能是我们预期的情况,因此我们可以计算得到CF等位基因频率:
p <- (9+842/2)/23369得到等位基因频率约为1.8%
现在,我们有了一个等位基因频率值(从样本中估计的种群频率),它是直接从观测数据计算出来的。在哈代-温伯格原理的假设下,我们期望可以用公式2p(1-p)从这个等位基因频率计算出杂合子的数量。因此,我们预期的携带者频率可以计算为:
2*p*(1-p)我们得到: 0.03636809
这意味着我们预期大约有3.64%的个体是CF等位基因的携带者。 这与实际观测到的杂合子基因型频率相比如何?在23,369名接受筛查的人中,共观察到842名杂合子。即842/23,369,约等于0.03603,或大约3.6%。预期值和观测值之间的差异非常小。让我们对镰状细胞贫血(SC)和β-地中海贫血(βT)进行相同的计算,我们可以看到2p(1-p)是观测到的杂合子频率的一个非常好的预测器。
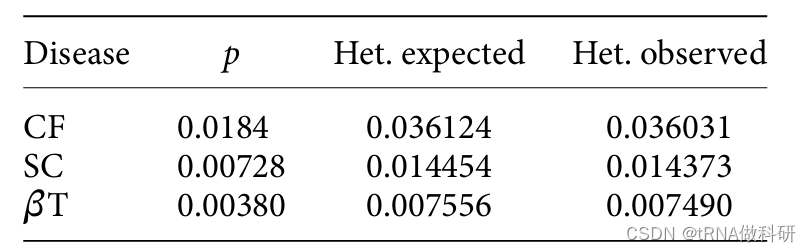
顺便说一下,我们还可以看到,对于隐性遗传疾病,携带者的频率(杂合子)远高于受影响个体的频率(纯合子)。这符合哈代-温伯格预测。杂合子与纯合子的比例预计为:
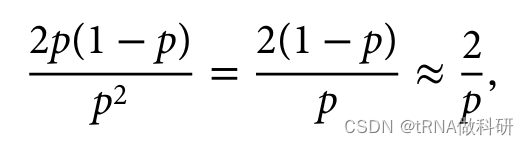
如果说p的值非常小,那么1-p的值就接近为1
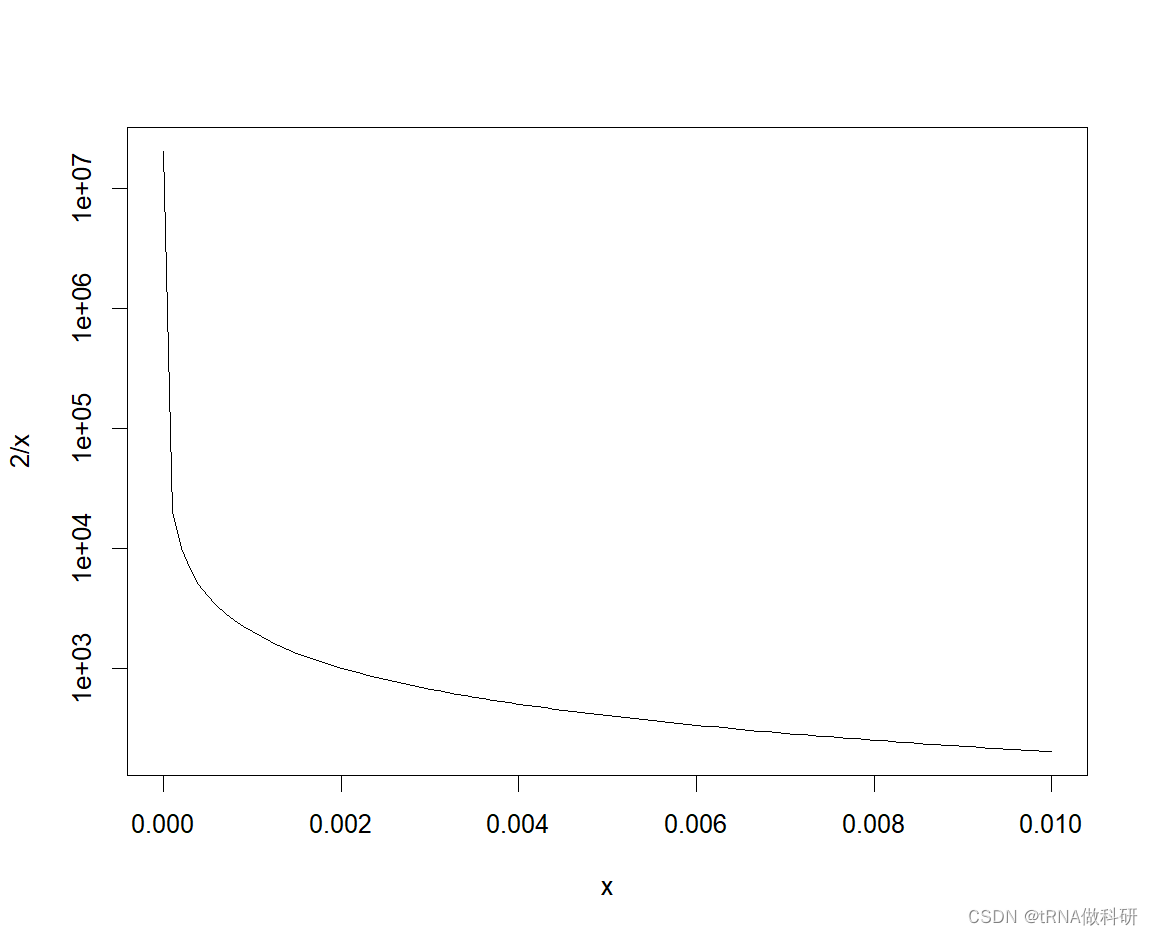
从数据库进行计算
我们使用popgenr数据集,我们首先得安装,我们使用两种方式:
如果可以直接下载,则:
install.packages("popgenr")
library("popgenr")如果下载不成功可以手动安装,官网下载包,把安装包放到路径中
CRAN: Package popgenr (r-project.org)
getwd()
install.packages("popgenr_0.2.tar.gz",repos=NULL)
library("popgenr")这个snp数据集来自人类基因组的二十五个随机采样的等位基因和基因型频率,现在应该作为对象snp加载。这个snp数据集是从1000 Genomes项目(http://www.internationalgenome.org)中提取的,这是一个全球已知人类遗传变异的公共库。
data(snp)
str(snp)
对于分类变量,我们可以进行可视化:
对于R语言的统计知识,可以看我的博客:
【R语言从0到精通】-3-R统计分析(列联表、独立性检验、相关性检验、t检验)_r 列联表分析-CSDN博客
plot(snp$type)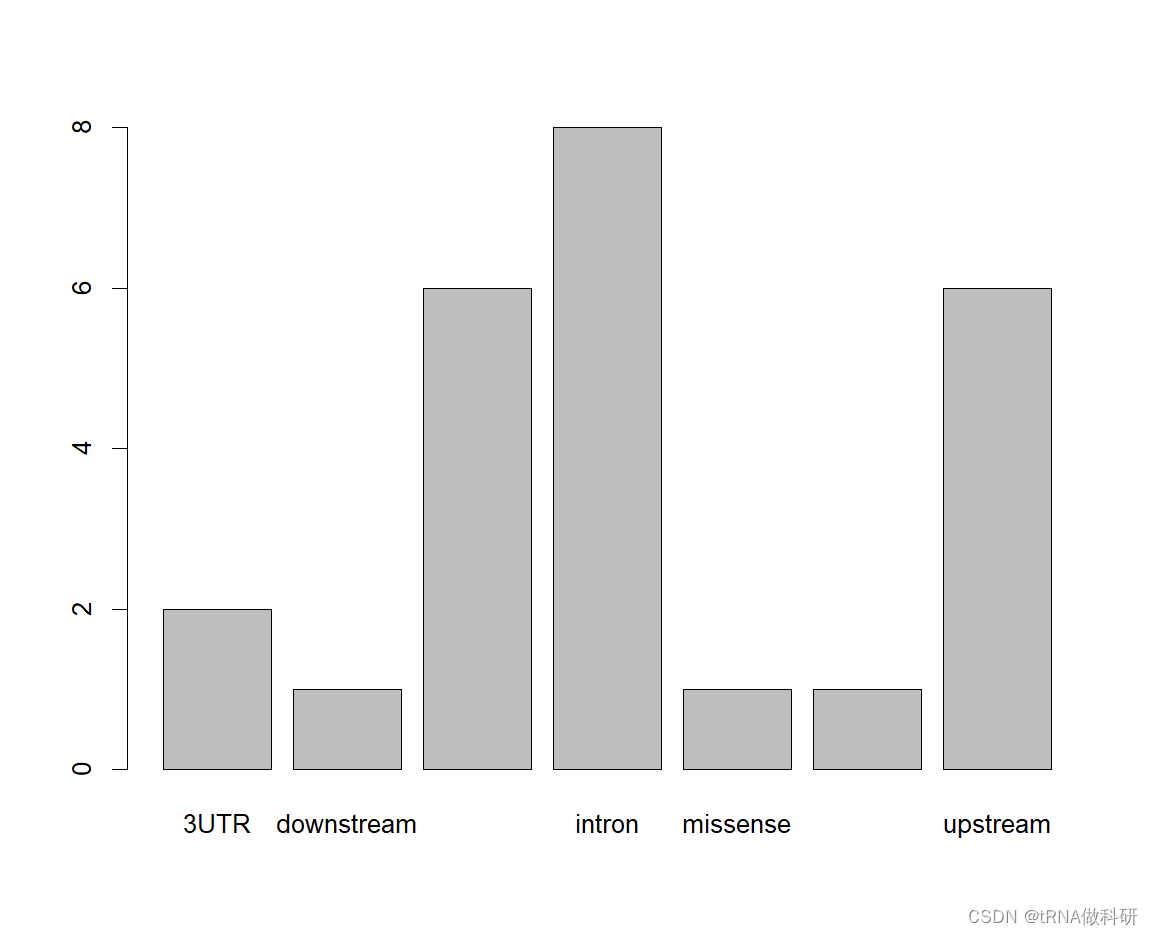
我们还是对于数据进行哈代温伯格预测与实际对照:
plot(0, 0, type="n", xlim=c(0, 1), ylim=c(0, 1),
xlab="Allele frequencies", ylab="Genotype frequencies")
curve(x^2, 0, 1, col="green", lwd=2, add=TRUE)
text(0.6, 0.2, "Homozygotes", col="green")
curve(2*x*(1-x), 0, 1, col="blue", lwd=2, add=TRUE)
text(0.25, 0.5, "Heterozygotes", col="blue")
points(snp$p, snp$hom, pch = 19, col = "green")
points(snp$p, snp$het, pch = 19, col = "blue")
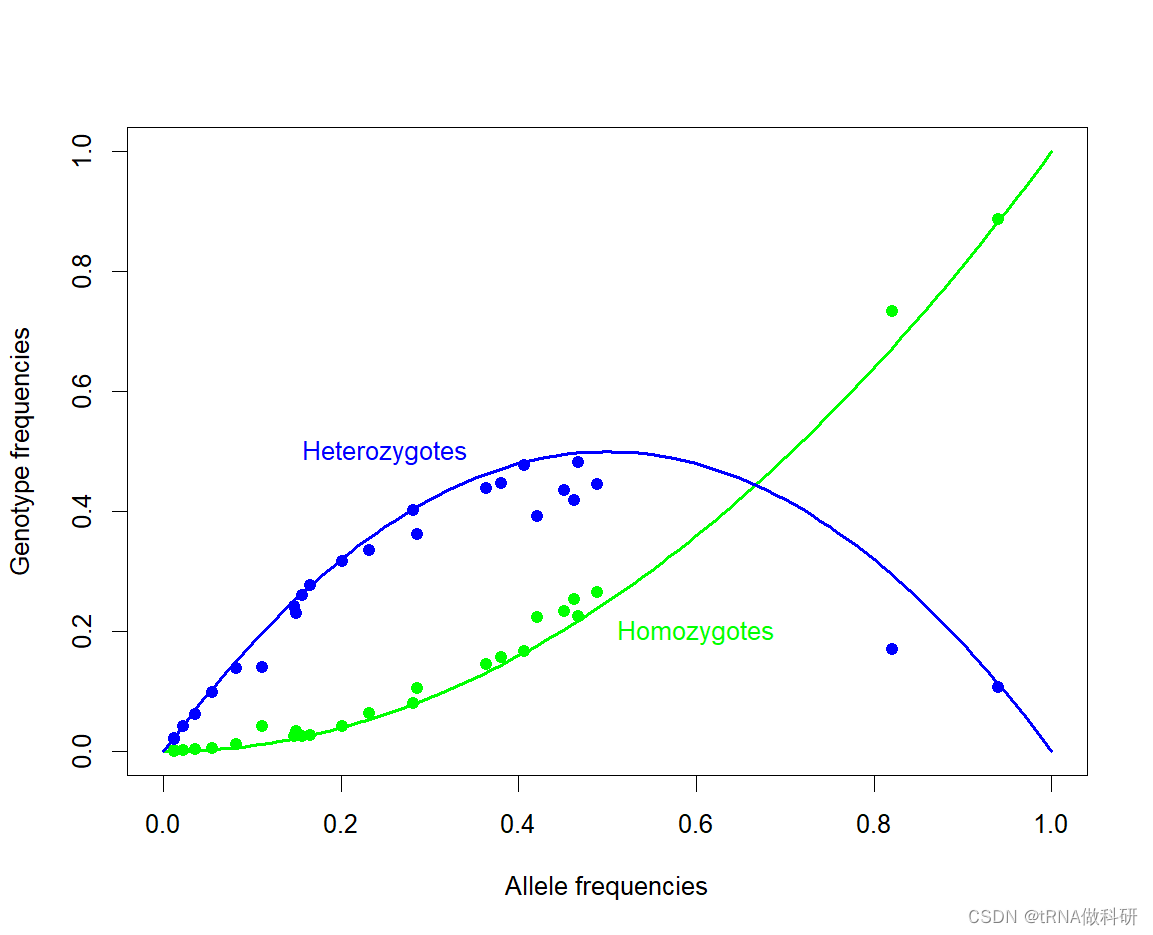
总体而言,预测和测量数据之间似乎有很好的一致性。几个特点显而易见。与预测的偏差通常表现为杂合性较低,纯合性较高。这与人口统计学效应一致,例如不同种群间等位基因频率的差异,这将在后面更详细地讨论。此外,注意到图中大多数点的等位基因频率小于50%;这是因为我们正在绘制的变异是由突变产生的新的等位基因变异(衍生状态),这些变异来自于预先存在的遗传序列(通过与人类最近的亲属比较确定的祖先状态),这些变异往往开始时相当罕见。当我们开始预测等位基因频率的随机波动并讨论遗传漂移的概念时,我们将再次回顾这个想法。