图

一、数据结构介绍

作为指针三剑客之三，图是树的升级版。图通常分为有向（directed）或无向（undirected），有循环（cyclic）或无循环（acyclic），所有节点相连（connected）或不相连（disconnected）。树即是一个相连的无向无环图，而另一种很常见的图是有向无环图（Directed Acyclic Graph，DAG）。

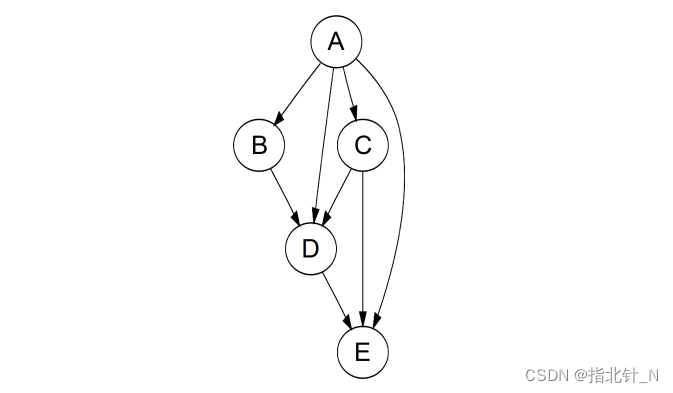
图通常有两种表示方法。假设图中一共有 n 个节点、m 条边。

第一种表示方法是邻接矩阵（adjacency matrix）：我们可以建立一个 n× n 的矩阵 G，如果第 i 个节点连向第 j 个节点，则 G[i][j] = 1，反之为 0；如果图是无向的，则这个矩阵一定是对称矩阵，即 G[i][j] = G[j][i]。

第二种表示方法是邻接链表（adjacency list）：我们可以建立一个大小为 n 的数组，每个位置 i 储存一个数组或者链表，表示第 i 个节点连向的其它节点。邻接矩阵空间开销比邻接链表大，但是邻接链表不支持快速查找 i 和 j 是否相连，因此两种表示方法可以根据题目需要适当选择。除此之外，我们也可以直接用一个 m × 2 的矩阵储存所有的边。

二、经典问题

1. 二分图

二分图算法也称为染色法，是一种广度优先搜索。如果可以用两种颜色对图中的节点进行着色，并且保证相邻的节点颜色不同，那么图为二分。

785. 判断二分图

785. Is Graph Bipartite?

        存在一个无向图，图中有 n 个节点。其中每个节点都有一个介于 0 到 n - 1 之间的唯一编号。给你一个二维数组 graph ，其中 graph[u] 是一个节点数组，由节点 u 的邻接节点组成。形式上，对于 graph[u] 中的每个 v ，都存在一条位于节点 u 和节点 v 之间的无向边。该无向图同时具有以下属性：
        不存在自环（graph[u] 不包含 u）。
        不存在平行边（graph[u] 不包含重复值）。
        如果 v 在 graph[u] 内，那么 u 也应该在 graph[v] 内（该图是无向图）
        这个图可能不是连通图，也就是说两个节点 u 和 v 之间可能不存在一条连通彼此的路径。
        二分图定义：如果能将一个图的节点集合分割成两个独立的子集 A 和 B ，并使图中的每一条边的两个节点一个来自 A 集合，一个来自 B 集合，就将这个图称为二分图。

如果图是二分图，返回 true ；否则，返回 false 。

利用队列和广度优先搜索，我们可以对未染色的节点进行染色，并且检查是否有颜色相同的相邻节点存在。注意在代码中，我们用 0 表示未检查的节点，用 1 和 2 表示两种不同的颜色。

注意输入的是邻接链表表示的图。

class Solution {
public:
    bool isBipartite(vector<vector<int>>& graph) {
        int n = graph.size();
        if(n == 0)  return true;
        vector<int> color(n, 0);
        queue<int> q;
        for(int i=0; i<n; ++i){
            if(color[i] == 0){
                q.push(i);
                color[i] = 1;
            }
            while(!q.empty()){
                int node = q.front();
                q.pop();
                for(const int& j: graph[node]){
                    if(color[j] == 0){
                        q.push(j);
                        color[j] = color[node] == 2? 1: 2;
                    }else if(color[j] == color[node]){
                        return false;
                    }
                }
            }
        }
        return true;
    }
};

2. 拓扑排序

拓扑排序（topological sort）是一种常见的，对有向无环图排序的算法。给定有向无环图中的 N 个节点，我们把它们排序成一个线性序列；若原图中节点 i 指向节点 j，则排序结果中 i 一定在 j 之前。拓扑排序的结果不是唯一的，只要满足以上条件即可。

210. 课程表 II

210. Course Schedule II

现在你总共有 numCourses 门课需要选，记为 0 到 numCourses - 1。给你一个数组 prerequisites ，其中 prerequisites[i] = [ai, bi] ，表示在选修课程 ai 前必须先选修 bi 。

例如，想要学习课程 0 ，你需要先完成课程 1 ，我们用一个匹配来表示：[0,1] 。
返回你为了学完所有课程所安排的学习顺序。可能会有多个正确的顺序，你只要返回任意一种就可以了。如果不可能完成所有课程，返回一个空数组。

我们可以先建立一个邻接矩阵表示图，方便进行直接查找。这里注意我们将所有的边反向，使得如果课程 i 指向课程 j，那么课程 i 需要在课程 j 前面先修完。这样更符合我们的直观理解。拓扑排序也可以被看成是广度优先搜索的一种情况：我们先遍历一遍所有节点，把入度为 0 的节点（即没有前置课程要求）放在队列中。在每次从队列中获得节点时，我们将该节点放在目前排序的末尾，并且把它指向的课程的入度各减 1；如果在这个过程中有课程的所有前置必修课都已修完（即入度为 0），我们把这个节点加入队列中。当队列的节点都被处理完时，说明所有的节点都已排好序，或因图中存在循环而无法上完所有课程。

class Solution {
public:
    vector<int> findOrder(int numCourses, vector<vector<int>>& prerequisites) {
        vector<vector<int>> graph(numCourses, vector<int>());
        vector<int> indegree(numCourses, 0);
        vector<int> res;
        for(auto& prerequisite: prerequisites){
            graph[prerequisite[1]].push_back(prerequisite[0]);
            ++indegree[prerequisite[0]];
        }
        queue<int> q;
        for(int i=0; i<indegree.size(); ++i){
            if(indegree[i] == 0){
                q.push(i);
            }
        } 
        while(!q.empty()){
            int u = q.front();
            q.pop();
            res.push_back(u);
            for(auto& v: graph[u]){
                --indegree[v];;
                if(indegree[v] == 0){
                    q.push(v);
                }
            }
        }
        for(int i=0; i<indegree.size(); ++i){
            if(indegree[i]){
                return vector<int>();
            }
        }
        return res;
    }
};