1. 矩阵的本质：

矩阵本质上是一种数学结构，它由按照特定规则排列的数字组成，通常被表示为一个二维数组。矩阵可以用于描述一组数据，或者表示某种关系，比如线性变换。

在人工智能中，矩阵常被用来表示数据集合，例如图像的像素值、文本的词频、用户行为等。通过矩阵，可以将这些复杂的数据结构化，并进行进一步的分析和处理。

矩阵（Matrix）：矩阵是数值的矩形阵列，通过特定的运算规则（如矩阵乘法），在数学、科学及工程领域中实现数据变换和问题解决的关键工具。

一、定义

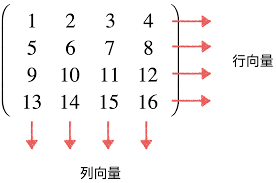
矩阵是一个数值的矩形阵列，它在数学、物理学、工程学和计算机科学等多个领域中都有广泛应用。矩阵由行和列组成，每个元素在矩阵中都有确定的位置。

二、符号表示

矩阵通常用大写的粗体字母表示，例如A、B、C等。矩阵的尺寸由其行数和列数决定，一个m×n的矩阵表示它有m行和n列。

矩阵中的每个数值被称为元素。元素的位置由其所在的行和列决定，通常用下标表示。例如，在矩阵A中，第i行第j列的元素可以表示为A[i][j]。

三、矩阵乘法

矩阵乘法是一种特殊的运算，不同于常规的元素间乘法。对于两个矩阵A和B，只有当A的列数等于B的行数时，它们才能进行矩阵乘法。结果矩阵C的尺寸是A的行数乘以B的列数。

矩阵乘法的计算遵循以下步骤：

验证矩阵A的列数是否等于矩阵B的行数。如果不相等，则无法进行矩阵乘法。

创建一个新的矩阵C，其行数与矩阵A相同，列数与矩阵B相同。

对于矩阵C中的每个元素C[i][j]，计算它是矩阵A的第i行与矩阵B的第j列的对应元素乘积之和。即，C[i][j] = A[i][k1] * B[k1][j] + A[i][k2] * B[k2][j] + … + A[i][kn] * B[kn][j]，其中k1, k2, …, kn是矩阵A的列索引或矩阵B的行索引。

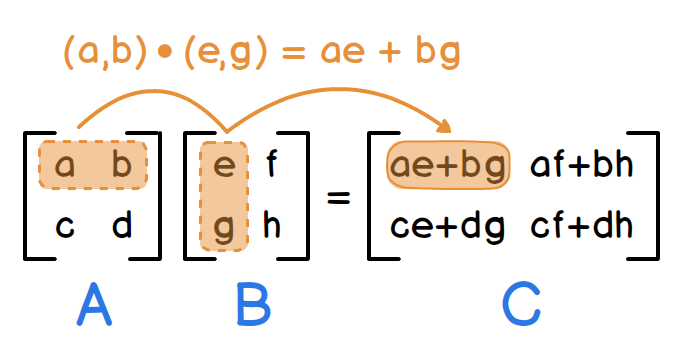
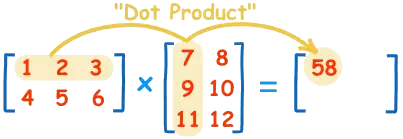
点积（Dot Product）：点积作为向量间的一种基本运算，通过对应元素相乘后求和来刻画两向量的相似度和方向关系。

2. 矩阵的原理：

矩阵的原理基于线性代数。在矩阵中，每个元素都可以由其行号和列号唯一确定。矩阵的加法、乘法、转置等运算满足一系列规则，这些规则构成了矩阵运算的基础。

• 矩阵加法：对应元素相加。
• 矩阵乘法：矩阵乘法不是简单的元素相乘，而是行乘以列的总和。
• 矩阵转置：将矩阵的行和列互换。

这些基本运算使得矩阵成为了处理和分析数据的强大工具，在人工智能领域中被广泛应用。

3. 矩阵的应用：

在人工智能中，矩阵有许多应用，其中一些主要的包括：

• 神经网络：神经网络中的权重和偏置通常被表示为矩阵，通过矩阵乘法和激活函数的组合实现输入数据的非线性变换和特征提取。

• 图像处理：图像可以表示为像素值的矩阵，通过矩阵运算可以实现图像的滤波、变换、降噪等操作。

• 自然语言处理：文本数据可以表示为词袋模型或词嵌入矩阵，通过矩阵运算可以进行文本分类、情感分析、语义理解等任务。

• 推荐系统：用户-物品评分矩阵用于表示用户对物品的偏好，通过矩阵分解等方法可以实现个性化推荐。