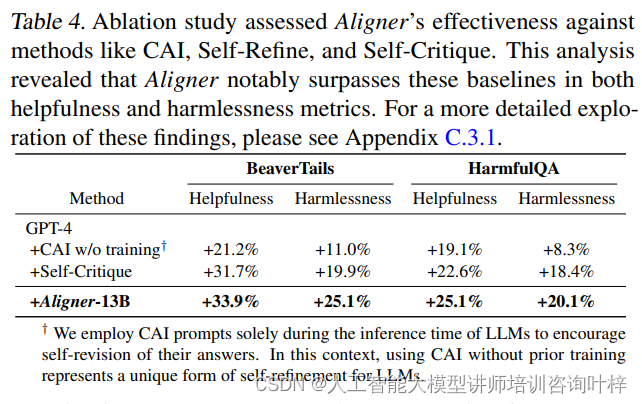
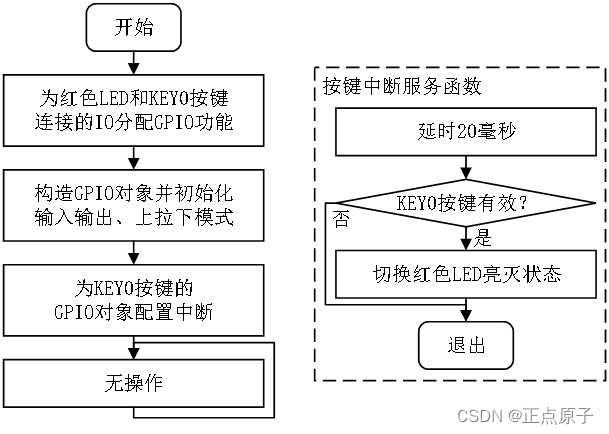
以下的图均只考虑二维，且没有切应力，有切应力的情况可以转换成只有两个正应力的情况，另外，这里画出的图均认为相当应力就是许用应力

第一，二强度理论用于脆性材料

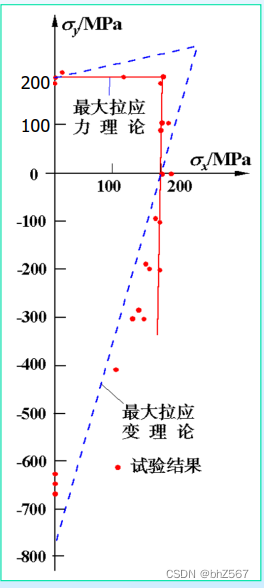
两种强度理论的图均明显有一个转角，这是因为主应力的转变，当，；当，

绘制最大拉应变理论的代码如下

mu=0.3;%泊松比
sigma=200;%许用应力
x1=sigma/(1-mu);%两条线交点
x=0:x1/10:x1;
y1=sigma+mu.*x;
y2=-sigma/(mu)+x./(mu);
figure;
plot(x, y1, 'r--', 'LineWidth', 2); 
  
% 保持当前图形，以便添加更多线  
hold on;  
  
% 绘制y2，使用蓝色虚线  
plot(x, y2, 'b--', 'LineWidth', 2); % 'b--'表示蓝色虚线  
  
% 添加网格  
grid on;  
  
% 添加x和y坐标轴标签  
xlabel('x');  
ylabel('y');  
% 显示图例（如果需要）  
legend('y1', 'y2');  

---

第三，四强度理论用于脆性材料

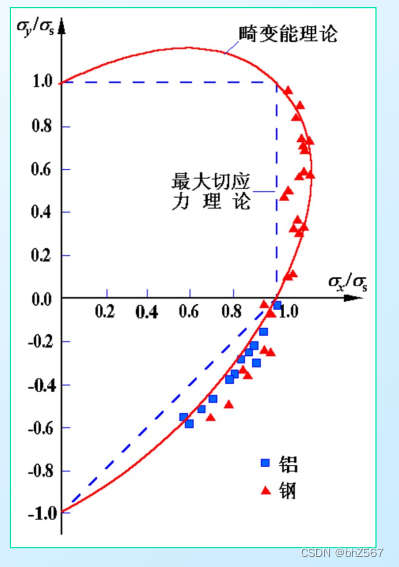
这里绘制畸变能理论的图，公式为，用极坐标代替得

绘图代码如下

% 定义theta的范围和步长，为了只画右半部分 
theta = linspace(-pi/2, pi/2, 500);
  
% 计算对应的r值  
r = sqrt(2 ./ (2 - sin(2*theta))); % 注意使用./进行元素间除法  
  
% 绘制极坐标图像   
polarplot(theta, r);  
title('r^2 = 2 / (2 - sin(2\theta))');  
grid on;  
% 将极坐标转换为直角坐标
x = r .* cos(theta);
y = r .* sin(theta);

% 绘制直角坐标图像
figure; % 创建一个新的图形窗口
plot(x, y); % 绘制x和y的图形
title('r^2 = 2 / (2 - sin(2\theta)) in Cartesian coordinates');%直接将theta转变为θ
xlabel('\sigma_x/\sigma_s');%可以显示Latex语句
ylabel('\sigma_y/\sigma_s');
grid on; % 显示网格
axis equal; % 设置坐标轴比例相等，以便图形不会变形

从图形上看，在极坐标系下的和在直角坐标系下的相同