矩阵和标量的运算
,则
矩阵与矩阵相乘
的矩阵A,
的矩阵B。两矩阵
,结果为
的矩阵,第一个矩阵的列数必须和第二个矩阵的行数相同,否则不能相乘
,
中的每个元素等于A的第i行所对应的矢量和B的第j列所对应的矢量进行矢量点乘的结果
即
注意:矩阵乘法不满足交换律
矩阵乘法满足结合律
Shader中常用矩阵
1.方块矩阵(方阵)(square matrix):行数和列数相等的矩阵。
2.对角矩阵:如果一个方阵除了对角元素外的所有元素都为0,那么这个方阵为对角矩阵。
3.单位矩阵:特殊的对角矩阵,用表示,例如
的单位矩阵为
。
4.转置矩阵:原矩阵为
,它的转置表示为
,转置矩阵的运算为原矩阵的第
行变成第
列,第
列变成第
行。
,示例
转置矩阵常用性质
性质一:矩阵转置的转置等于原矩阵
性质二:矩阵串接的转置等于反向串接各个矩阵的转置
5.逆矩阵
给定一个矩阵,它的逆矩阵为
,把
和
相乘,结果为一个单位矩阵,即
矩阵有逆矩阵的前提为该矩阵为方阵且并非所有元素都为0。
逆矩阵的常用性质
性质一:逆矩阵的逆矩阵是原矩阵本身,即
性质二:单位矩阵的逆矩阵是它本身,即
性质三:转置矩阵的逆矩阵是逆矩阵的转置,即
性质四:矩阵串接相乘后的逆矩阵等于反向串接各个矩阵的逆矩阵,即
三维变换与投影
现实世界是三维的,要在二维屏幕上绘制出三维场景需要通过投影变换降低维数。
三维变换矩阵
三维变换引入齐次坐标,在四维空间内进行研究。
三维变换可表示为某一变换矩阵与物体顶点集合的齐次坐标矩阵相乘的形式,三维变换矩阵是的方阵。
例如:
为
的子矩阵,用于对物体进行比例、旋转、反射、错切变换。
为
的子矩阵,用于对物体进行平移变换。
为
子矩阵,用于对物体进行投影变换。
为
子矩阵,用于对物体进行整体比例变换。
三维变换形式
三维变换的基本方法是把矩阵作为算子,作用到变换前的物体顶点集合的齐次坐标矩阵上,得到变换后新的顶点集合的齐次坐标矩阵,连接新的物体顶点,可绘制出变换后的三维物体模型。
设变换前的物体顶点矩阵
变换后的物体顶点矩阵
则三维变换公式为,即
三维基本变换
三维基本变换是指将点从一个坐标位置变换到另一个坐标位置
的过程,是相对于坐标系或坐标轴进行的几何变换。
平移变换
、
、
为平移参数
平移变换的坐标表示为
三维平移变换矩阵为
比例变换
、
、
为比例系数
比例变换的坐标表示为
三维比例变换矩阵为
旋转变换
三维旋转变换一般看作二维旋转变换的组合,可分为绕轴旋转、绕
轴旋转、绕
轴旋转,绕坐标轴旋转角用
表示,
正向定义符合右手螺旋定则,大拇指指向旋转轴正向,其余四指的转向为转角的正向。
绕 轴旋转
轴旋转
为正向旋转角
绕轴旋转变换的坐标表示为
绕轴旋转三维变换矩阵为
绕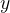 轴旋转
轴旋转
为正向旋转角
绕轴旋转变换的坐标表示为
绕轴旋转三维变换矩阵为
绕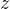 轴旋转
轴旋转
为正向旋转角
绕轴旋转变换的坐标表示为
绕轴旋转三维变换矩阵为
反射变换
三维反射分为关于坐标轴的反射和关于坐标平面的反射两类。
关于 轴的反射
轴的反射
关于轴反射变换的坐标表示为
关于轴的三维反射变换矩阵为
关于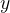 轴的反射
轴的反射
关于轴反射变换的坐标表示为
关于轴的三维反射变换矩阵为
关于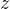 轴的反射
轴的反射
关于轴反射变换的坐标表示为
关于轴的三维反射变换矩阵为
关于 平面的反射
平面的反射
关于平面反射变换的坐标表示为
关于平面的三维反射变换矩阵为
关于 平面的反射
平面的反射
关于平面反射变换的坐标表示为
关于平面的三维反射变换矩阵为
关于 平面的反射
平面的反射
关于平面反射变换的坐标表示为
关于平面的三维反射变换矩阵为







![[寄宿日记]韩漫日漫无删减完整版,免费在线观看漫画](https://img-blog.csdnimg.cn/direct/8c4cced528ca43499e1e6a9be52df94f.jpeg)