计算几何系列——XCPC中计算几何一些题型杂谈(中)

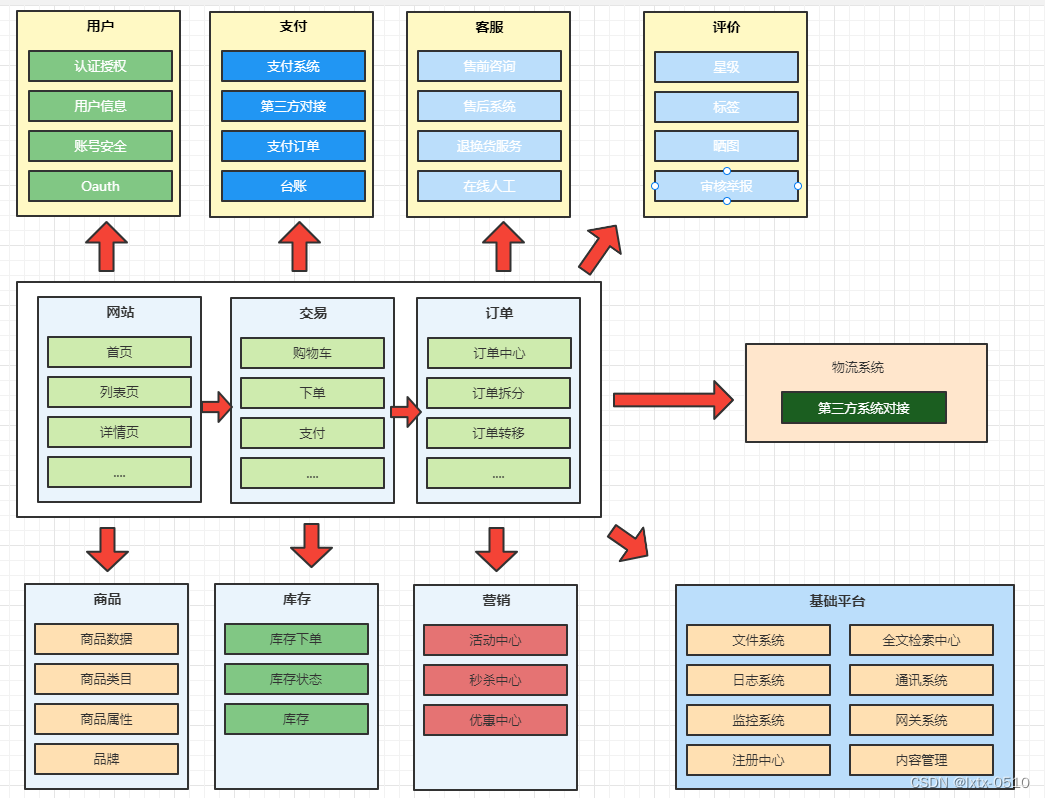
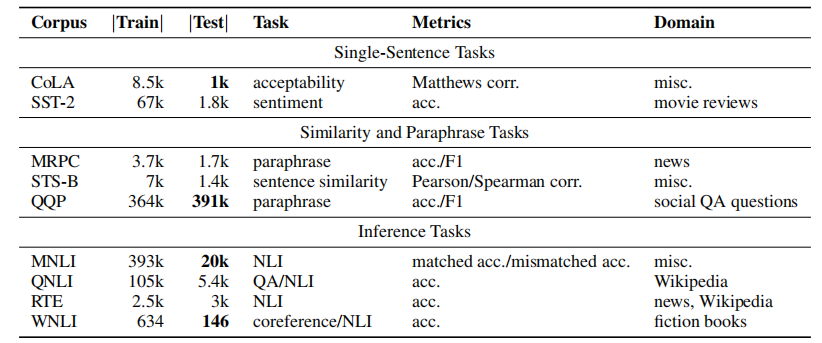
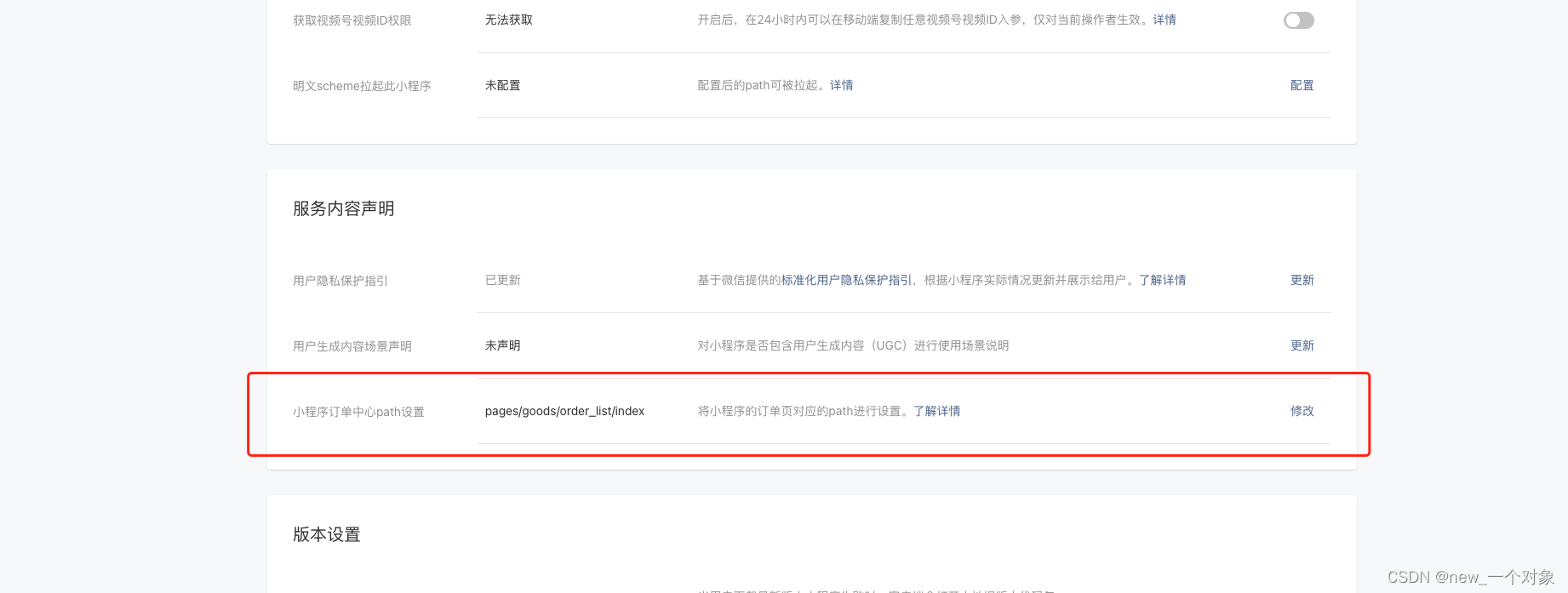
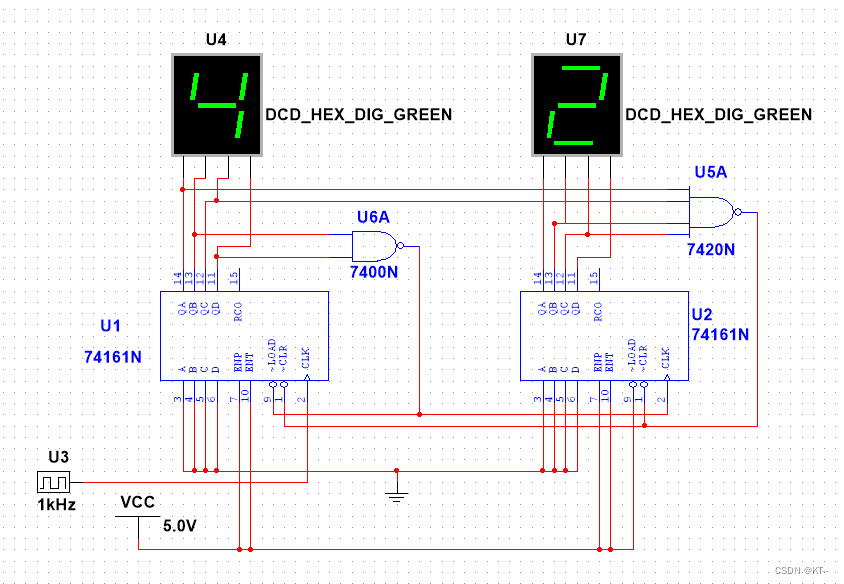
本系列文章力求以简洁易懂的文字介绍计算几何中的基本概念，使读者快速入门，故不追求难度和深度，仅起到抛砖引玉的作用。

在XCPC中有一种题叫计算几何，这类题在大多数时候都作为一类金牌题甚至防AK题的难度出现，但是在前段时间我写了许多学习计算几何的博客，会发现计算几何的知识体系十分独立且庞大，而且板子很长，就是一个特点：毒瘤。

所以，在这里，我作为一个主修计算几何的ACMer，做了一点点题后对这类毒瘤题做出了一定的总结，希望对大家能有所帮助。首先，计算几何的题目并非全是难题，它也有一个难度梯度，我这边将其分为差不多三类题：

1.一般的平面几何知识的运用，一般这类题难度较低，需要掌握基本的几何知识和计算几何代码能力即可,一般这类题一般作为XCPC的铜牌难度及以下,在大多数省赛中作为一个区分水平的题目。

2.与一些ACM的惯用算法及数据结构以及一些几何算法考在一起的较难题,这类题一般作为XCPC中的银牌题至金牌题中出现,具有较高的区分度。

3.一类考的比较多的经典题型:寻找某一个参数,可能是一个点,一条直线,用于满足一个特定函数的极值或者求某些参数的几何期望。这类题的难度一般放在XCPC中的防ak机制中,做法较为明确但是由于代码的复杂程度与精度的设置导致一般通过率很低。

在这里告诉大家笔者的计算几何水平十分一般,少有能在赛时写出来这种,但是还是有一些不错的经验,赛时赛后也是苦苦钻研的这类题,有些不错的题目给大家讲解下😄:

这节一共三类题，讲完这个第二类的先差不多，第一是平面网格化，第二类是时针顺序扫描思想，第三是旋转中的连锁反应需要结合下线段树。O(∩_∩)O

第二类 : 几何问题同时涉及一些XCPC基本算法的较难题

T4：平面网格化

对于平面网格化，我们可以使用一道非常简短的问题来引入：

(平面邻点对). 给定平面中一点集 S, |S | = n，求欧氏距离下最近的一对点。

我给这道题，洛谷上的平面最近点对的n设置满足O(n^2)的算法，所以我在这里对其加强改成：2 <= n <= 1000000。这样我们需要设置一个O(n)的算法来解决这个问题，一般像这个数据量的查找问题我们还是往随机增量的方向思考。所以有一下想法：

考虑随机增量法，随机打乱后按顺序加入所有点，若当前已经得到的最小距离为 d，把平面按照 d 细分成网格，即点 (x, y) 将被分到第 (⌊ x/d ⌋,⌊ y/d ⌋) 格中。———— 平面网格化

注意到，此时每格仅有 O(1) 个点分配其中，否则答案会取得更小。考虑加入新的一个点 (x, y)，其在格子 (a, b) 中，则考虑其引起的答案的更新，只需要考虑所有 (a ± 1, b ± 1) 格子中的所有 O(1) 个点即可，访问只需要 hash 表和链表。若此时更新了答案，则重构网格划分，将当前的所有点重新添加进对应的 hash 表。

考虑时间复杂度，第 i 次更新答案的概率应为 O(1 / i)（考虑一张 n 个点的图，两两之间有形成排列的边权，第 i 次加入的点与之前的点连边更小的概率可以考虑将这一个点依次替换为之前的 i 个点进行平均），故期望为 ∑O( 1 / i · i) · O(1) = O(n)

回顾我们的思路，对于距离这样的问题，最好的刻画其实是圆，但是圆既不好表示，完整的划分整个平面，于是我们采用正方形去近似的表达我们的刻画，这样既划分了平面，又得到了某种几何性质，然后依据这样的较为连续的性质我们又能使用数据结构去维护。

考虑确定网格化的方式，除了随机增量确定边长，我们还可以通过二分的方式确定边长及答案。二分网格化之后，我们可以先把其中至少有三个点的正方形网格用正方形盖住，而后只需考虑未被盖住的点，考虑这个点能够形成的正方形数量，以这个点为某个角的正方形共计 4 个，其中每个都有不多于 1 个点（否则可直接覆盖这个点），那么总共可能包含的三个点的数量也就只有 O(1) 种，至于找到那 4 个正方形中的点，其只需暴力检查其四周的网格中的点即可，容易证明这样做是 O(n) 的，加上二分总时间复杂度是 O(n log n)。

所以化简出来的一个做法就是：分治法，平面网格随机增量，玄学法，则三个写法都给你：

👇这是经典几何分治求法：

#include<bits/stdc++.h>
#define Alex std::ios::sync_with_stdio(false),std::cin.tie(0),std::cout.tie(0);
#define int long long
#define double long double
const int QAQ = 0;
const int mod = 1e9 + 7;
const double eps = 1e-10;
const int N = 1000005;
const int inf = 2 << 20;
int n,T[N];
struct Point{
	double x,y;
};
Point S[N];
inline bool cmp(const Point &x,const Point &y)
{
	if(x.x == y.x)
	{
		if(x.y < y.y) return true;else return false;
	}else
	{
		if(x.x < y.x) return true;else return false;
	}
}
inline bool cmpS(const int &x,const int &y)
{
	if(S[x].y < S[y].y) return true;else return false;
}
inline double min(double x,double y)
{
	if(x < y) return x;else return y;
}
inline double dist(int x,int y)
{
	double d1 = (S[x].x - S[y].x) * (S[x].x - S[y].x);
	double d2 = (S[x].y - S[y].y) * (S[x].y - S[y].y);
	return std::sqrt(d1 + d2);
}
inline double dist(Point A,Point B)
{
	double d1 = (A.x - B.x) * (A.x - B.x);
	double d2 = (A.y - B.y) * (A.y - B.y);
	return std::sqrt(d1 + d2);
}
inline double Merge(int l,int r)
{
	double ans = inf;
	if(l == r) return ans;
	if(l + 1 == r) return dist(l,r);
	int mid = (l + r) >> 1;
	double d1 = Merge(l,mid);
	double d2 = Merge(mid + 1,r);
	ans = min(d1,d2);
	int k = 0;
	for(int i = l;i <= r;i++)
	if(std::fabs(S[mid].x - S[i].x) < ans) T[k++] = i;
	std::sort(T,T + k,cmpS);
	for(int i = 0;i <= k - 1;i++)
	for(int j = i + 1;j < k && S[T[j]].y - S[T[i]].y < ans;j++)
	{
		double d3 = dist(T[i],T[j]);
		ans = min(ans,d3);
	}
	return ans;
}
signed main()
{
	Alex;
	int _ = 1;
	while(_--)
	{
		std::cin>>n;
		for(int i = 0;i <= n - 1;i++) std::cin>>S[i].x >>S[i].y;
		std::sort(S,S + n,cmp);
		double ans = Merge(0,n - 1);
		std::cout<<std::fixed<<std::setprecision(15)<<ans<<'\n';
	}
}

👇这是一种玄学的做法：

#include<bits/stdc++.h>
#define Alex std::ios::sync_with_stdio(false),std::cin.tie(0),std::cout.tie(0);
#define int long long
#define double long double
const int QAQ = 0;
const int mod = 1e9 + 7;
const double eps = 1e-10;
const int N = 1000005;
const int inf = 2 << 20;
int n,T[N];
struct Point{
	double x,y;
};
Point S[N];
inline bool cmp(const Point &x,const Point &y)
{
	if(x.x == y.x)
	{
		if(x.y < y.y) return true;else return false;
	}else
	{
		if(x.x < y.x) return true;else return false;
	}
}
inline bool cmpS(const int &x,const int &y)
{
	if(S[x].y < S[y].y) return true;else return false;
}
inline double min(double x,double y)
{
	if(x < y) return x;else return y;
}
inline double dist(int x,int y)
{
	double d1 = (S[x].x - S[y].x) * (S[x].x - S[y].x);
	double d2 = (S[x].y - S[y].y) * (S[x].y - S[y].y);
	return std::sqrt(d1 + d2);
}
inline double dist(Point A,Point B)
{
	double d1 = (A.x - B.x) * (A.x - B.x);
	double d2 = (A.y - B.y) * (A.y - B.y);
	return std::sqrt(d1 + d2);
}
inline double Merge(int l,int r)
{
	double ans = inf;
	if(l == r) return ans;
	if(l + 1 == r) return dist(l,r);
	int mid = (l + r) >> 1;
	double d1 = Merge(l,mid);
	double d2 = Merge(mid + 1,r);
	ans = min(d1,d2);
	int k = 0;
	for(int i = l;i <= r;i++)
	if(std::fabs(S[mid].x - S[i].x) < ans) T[k++] = i;
	std::sort(T,T + k,cmpS);
	for(int i = 0;i <= k - 1;i++)
	for(int j = i + 1;j < k && S[T[j]].y - S[T[i]].y < ans;j++)
	{
		double d3 = dist(T[i],T[j]);
		ans = min(ans,d3);
	}
	return ans;
}
//signed main()
//{
//	Alex;
//	int _ = 1;
//	while(_--)
//	{
//		std::cin>>n;
//		for(int i = 0;i <= n - 1;i++) std::cin>>S[i].x >>S[i].y;
//		std::sort(S,S + n,cmp);
//		double ans = Merge(0,n - 1);
//		std::cout<<std::fixed<<std::setprecision(15)<<ans<<'\n';
//	}
//}
signed main()
{
	Alex;
	int _ = 1;
	while(_--)
	{
		std::cin>>n;
		for(int i = 0;i <= n - 1;i++) std::cin>>S[i].x >>S[i].y;
		std::sort(S,S + n,cmp);
		double ans = 2e18;
		for(int i = 0;i <= n - 2;i++)
		for(int j = 1;j <= 5;j++) ans = min(ans,dist(S[i],S[i + j]));
		std::cout<<std::fixed<<std::setprecision(4)<<ans<<'\n';
	}
}

👇随机增量法：

#include<stdio.h>
#include<algorithm>
#include<cmath>
using namespace std;
int n,len;
struct point{
	double x;
	double y;
} pointset[100005];
double ans=0,anans=9999999999;
double dis(point a,point b)
{
	return sqrt((a.x-b.x)*(a.x-b.x)+(a.y-b.y)*(a.y-b.y));
}
bool cmp2(point a,point b)
{
	return  a.x!=b.x?a.x<b.x:a.y<b.y;
}
void work()
{
	
	sort(pointset,pointset+n,cmp2);
	for(int i=0;i<n-1;i++)
		for(int j=i+1;j<n;j++)
		{
			anans=min(dis(pointset[i],pointset[j]),anans);
			if(pointset[j].x-pointset[i].x>anans)
			break;
		}
}
int main()
{
	int i,j,k;
	scanf("%d",&n);
	for(i=0;i<n;i++)
	scanf("%lf %lf",&pointset[i].x,&pointset[i].y);
	work();
	printf("%.4lf",anans);
	return 0;
}

然后这个思想我们还能推广到怎样的题目上呢？大家可以尝试去思考这些：

1. (BJWC2011 最小三角形). 给定平面上一点集 S, |S | = n, 求其中三个点组成的周长最小的三角形。

2.(正方形覆盖问题). 给定平面上一整点集 S, |S | = n, 你需要给出若干边长相等的正方形, 使得每个正方形至少盖住三个点, 且边与坐标轴平行, 并且顶点为整点, 并且所有点都至少被一个正方形盖住, 求正方形最小边长。

呃呃，这还有一题，网格水题，我觉得挺简单的，就是先对点进行时针排序，然后再用叉积进行面积计算即可，可以写写提升下代码能力，因为我赛时没写出来hhh：

----------------------------------------------------------我是分割线--------------------------------------------------------

T5：计算几何时针扫描线

题目来源：Problem - F - Codeforces

题意：给你二维平面上的n个点，然后每个点都向下发出一条射线，当一个点被射线扫描到时就会消失，然后射线的初始方向时-y轴的，经过逆时针的时针扫描后，请问平面上各点的消失序列，即需要你求出每个点的消失顺序。

题意建模出来就是：

👇初始时刻：其中，H，I，D，L，M都消失，我们算x的大小为第一关键字，y的大小为第二关键字排序这些同时消失的点。

👇：之后的某一时刻：呃呃字母有点难搞，之后消失的是E点，接着是F点......

👇：终末时刻：最终将只剩下点A存活：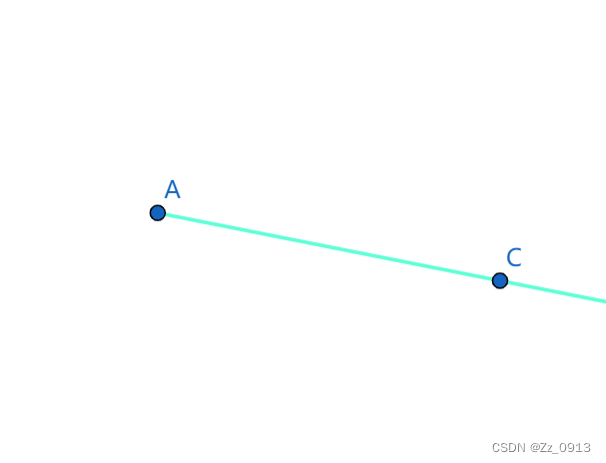

👆由上述的一个模拟过程我们可以获得一下信息：

Hint1：1.最终平面上一定只会剩下一个点。

2.由射线扫描的特性可知，对于同一个x = a上的若干个点（a , y1) (a , y2) (a , y3)...,一定是y最大的那个点或将最晚消失。

那么由这些信息我们可以的思路第一步就是：先把所有x相同上的点消除一遍，存入答案，剩下的点我们另寻解法：

    	cin>>n;
		for(int i = 1;i <= n;i++) cin>>a[i].x>>a[i].y;//输入
		vector<pair<int,int> > ans,V;
        set<pair<int,int> > S2;
        set<pair<double,int> > S1;
        for(int i = 1;i <= n;i++) ma[a[i].x].push_back(a[i].y);//用map存每个x坐标的映射点集
        for(auto i : ma)
        {
        	auto v = i.second;
        	sort(v.begin(),v.end());//这里排序的时间复杂度没问题
        	for(int j = 0;j + 1 < v.size();j++)
        	    ans.push_back({i.first,v[j]});//存入答案
        	V.push_back({i.first,v[v.size() - 1]});//保留最后一个存活点用于下一步操作
		}

Hint2：1.对于每个点，相对于它的点位消失的最快的一个点一定是两点构成直线斜率最小的一个点。

2.所有点之间都不在同一个x中，所以可以保证一个旋转过程中删点的唯一性（这一点可以读者进行模拟来更好的理解）

答：因此我们只要按斜率的从小到大删点即可，最佳做法是把点对放入两个Set中操作，具体代码如下：

#include<bits/stdc++.h>
#define Alex ios::sync_with_stdio(0),cin.tie(0),cout.tie(0);
#define LD long double
using namespace std;
const int QAQ = 0;
const int base = 131;
const int mod = 998244353;
const double eps = 1e-10;
int n;
map<int,vector<int> > ma;
struct Point{ int x,y; }a[500005];
inline bool cmp(const Point &x,const Point &y)
{
	if(x.x < y.y || x.x == y.x && x.y < y.y) return true;
	return false;
}
inline double K(pair<int,int> A,pair<int,int> B)
{
	int x1 = A.first,x2 = B.first;
	int yy = A.second,y2 = B.second;
	return (((double)y2 - (double)yy) / ((double)x2 - (double)x1));
}
signed main()
{
	Alex;
	int _;
	_ = 1;
	while(_--)
    {
    	cin>>n;
		for(int i = 1;i <= n;i++) cin>>a[i].x>>a[i].y;
		//sort(a + 1,a + n + 1,cmp);
		//a[n + 1].x = a[n].x + 1,a[n + 1].y + a[n].y + 1;
		vector<pair<int,int> > ans,V;
        set<pair<int,int> > S2;
        set<pair<double,int> > S1;
        for(int i = 1;i <= n;i++) ma[a[i].x].push_back(a[i].y);
        for(auto i : ma)
        {
        	auto v = i.second;
        	sort(v.begin(),v.end());
        	for(int j = 0;j + 1 < v.size();j++)
        	    ans.push_back({i.first,v[j]});
        	V.push_back({i.first,v[v.size() - 1]});
		}
//		for(int i = 1;i <= n;i++)
//		{
//			if(a[i].x != a[i + 1].x)
//			{
//				V.push_back({a[i].x,a[i].y});
//			}else
//			{
//				ans.push_back({a[i].x,a[i].y});
//			}
//		}
		sort(ans.begin(),ans.end());
		sort(V.begin(),V.end());
		for(int i = 0;i < V.size() - 1;i++) 
		    S1.insert({K(V[i],V[i + 1]),V[i + 1].first});
		for(auto i : V) 
		    S2.insert(i);
		while(! S1.empty())
		{
			int x = (*S1.begin()).second;
			S1.erase(S1.begin());
			auto it = S2.lower_bound({x,0});
			auto t1 = it,t2 = it;
			t1--,t2++;
			if(t2 != S2.end())
			{
				S1.erase({K((*it),(*t2)),(*t2).first});
				S1.insert({K((*t1),(*t2)),(*t2).first});
			}
			ans.push_back(*it);
			S2.erase(it);
		}
		for(auto i : ans) 
		    cout<<i.first<<' '<<i.second<<'\n';
    }
    return QAQ;
}

----------------------------------------------------------我是分割线--------------------------------------------------------

T6：计算几何+线段树

题目来源：2991 -- Crane (poj.org)

题意：就是说有一台起重机，然后看成了N条顺次链接的线段，第i条的长度为Li，在初始状态中所有的线段都笔直连接指向上方。然后输入给你C条指令包含两个整数Si，Ai，表示让Si到Si+1之间的角度变成Ai度。其中角度指线段Si开始沿逆时针旋转到Si+1所经过的角度。最开始时所有的角度都是180°。假设支点坐标为（0，0），要求你输出操作完成后起重机的第N条线段的端点坐标。

不理解的我给下两组数据的一个图示👇：

应该可以理解了叭，那么我就讲解下思路了捏~：我们将每一段视作一个向量，经过模拟可以发现，当向量i发生旋转时，比如旋转了α度，那么对于i + 1至n之间的所有向量都旋转了α度，那么有C个这样的一个向量转向，最后所求的答案就是所有向量相加。

这是所谓的一个结论图示👇：

那么这道题目的思路没啥问题了，就是说这个数据量为1e4那么就是说题目不允许我们使用O(n^2)的算法求解，那么就是说在这个从i ~ n个向量的角度变换过程我们不能线扫，而是使用什么？

那就是区间修改第一个想到的就是线段树，那么这道题就需要我们对向量集建立线段树，那么问题就迎刃而解了~，接下来我放上代码，并不是说这题有多难，只是讲解下这个XCPC中的计算几何是如何结合其它算法的（二类题）：

#include<bits/stdc++.h>
#define Alex std::ios::sync_with_stdio(false),std::cin.tie(0),std::cout.tie(0);
#define PI std::acos(-1)
#define int long long
#define double long double
const int QAQ = 0;
const int mod = 1e9 + 7;
int N, C;
int L[200005];
int pre[200005];
int s, a;
struct Node
{
    double vx;//区间向量的和向量的横坐标
    double vy;//区间向量的和向量的纵向量
    int start;//线段区间头
    int end;//区间尾
    double degree;//更新值
};
Node Tree[1000005];
inline void Build_Tree(int start,int end,int index)
{
    Tree[index].start = start;
    Tree[index].end = end;
    Tree[index].degree = 0;
    if(start == end - 1)
    {
        Tree[index].vx = 0;
        Tree[index].vy = 1.0 * L[start];
        return;
    }
    int mid = (start + end) >> 1;
    int left = (index << 1) + 1;
    int right = (index << 1) + 2;
    Build_Tree(start,mid,left);
    Build_Tree(mid,end,right);
    Tree[index].vx = Tree[left].vx + Tree[right].vx;
    Tree[index].vy = Tree[left].vy + Tree[right].vy;
    return;
}
inline void rotate_degree(double &x,double &y,double degree)
{
    double tmp_x = x;
    double tmp_y = y;
    x = tmp_x * std::cos(degree) - tmp_y * std::sin(degree);
    y = tmp_x * std::sin(degree) + tmp_y * std::cos(degree);
}
inline void push_down(int index)
{
    if(Tree[index].degree != 0)
    {
        double ang = Tree[index].degree;
        int left = (index << 1) + 1;
        int right = (index << 1) + 2;
        rotate_degree(Tree[left].vx, Tree[left].vy, ang);
        rotate_degree(Tree[right].vx, Tree[right].vy, ang);
        Tree[left].degree += ang;
        Tree[right].degree += ang;
        Tree[index].degree = 0;
    }
}
inline void Update(int s,double ang,int index)
{
    if(Tree[index].end <= s) return;
    if(s <= Tree[index].start)
    {
        Tree[index].degree += ang;
        rotate_degree(Tree[index].vx,Tree[index].vy, ang);
        return;
    }
    int left = (index << 1) + 1;
    int right = (index << 1) + 2;
    push_down(index);
    Update(s,ang,left);
    Update(s,ang,right);
    Tree[index].vx = Tree[left].vx + Tree[right].vx;
    Tree[index].vy = Tree[left].vy + Tree[right].vy;
    return;
}
signed main()
{
	Alex;
    int _;
	_ = 1;
	std::cin>>_;	
    while(_--)
    {
    	std::cin>>N>>C;
        for(int i = 0;i <= N - 1;i++)
        {
            std::cin>>L[i];
            pre[i] = 180;
        }
        Build_Tree(0, N, 0);
        for(int i = 0;i <= C - 1;i++)
        {
            std::cin>>s>>a;
            int r = a - pre[s - 1];
            pre[s - 1] = a;
            double ang = r * 1.0 / 360 *2 * PI;
            Update(s,ang,0); 
            std::cout<<std::fixed<<std::setprecision(15)<<Tree[0].vx<<' '<<Tree[0].vy<<std::endl;
        }
    }
    return 0;
}

OK，那么这类题所谓几何问题同时涉及一些XCPC基本算法的较难题的已经差不多讲了，如果还有一些巧妙的题目我会下次有机会单独领出来讲，这次讲解主要是一些经典的二类题。

给大家一些好题：

Problem - 934E - Codeforces

Problem - A - Codeforces

Problem - D - Codeforces

Attachments - 2017-2018 ACM-ICPC Southeast Regional Contest (Div. 1) - Codeforces

那么在下一节，也就是《计算几何系列——XCPC中计算几何一些题型杂谈(下)》中，差不多在7月中旬前出，因为笔者要被抓去军训了，不过这样我就好好思考整理一下这个三类题，是一类防AK题，基本上就是三种考察：

1.查找目标的几何值以满足某个函数的极值（常考）

2.求解几何期望值

那么这类题需要很强的数学推导能力，函数推导以及高等数学的基础知识支持，还有就是较高的代码能力，因此这讲我放缓进度，尽可能的希望所有读者都能掌握这类题的一个做法，后续就自己刷题了捏。那么暂时这段时间先做点叭~