贪心法思想

​ 基本思想是在问题的每个决策阶段，都选择当前看起来最优的选择，即贪心地做出局部最优的决策，以期获得全局最优解。

​ 正如其名字一样，贪心法在解决问题的策略上目光短浅，只根据当前已有的信息做出选择。一旦做出选择，不管将来有什么结果，这个选择都不会改变。

与动态规划对比：

​ 贪心算法和动态规划都常用于解决优化问题。它们之间存在一些相似之处，比如都依赖最优子结构性质，但工作原理不同。

• 动态规划会根据之前阶段的所有决策来考虑当前决策，并使用过去子问题的解来构建当前子问题的解。
• 贪心算法不会考虑过去的决策，而是一路向前地进行贪心选择，不断缩小问题范围，直至问题被解决。

举例-零钱兑换问题：

​ 贪心算法实现简单，易于理解，效率也很高，但是具有局限性。

有一组不同面额的硬币，给定一个总金额 𝑎𝑚𝑡 ，计算并返回可以凑成总金额所需的最少的硬币个数 。

每次贪心的选择尽可能大的硬币（不大于总金额的最大硬币），直至凑出目标金额为止。

硬币组合[100、50、10、5、1]，总金额amt为131：

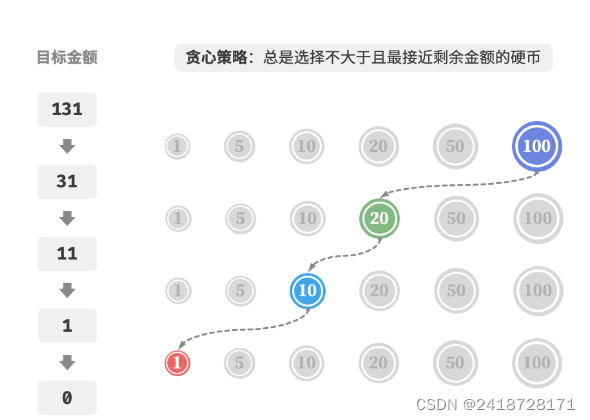
但是，某些情况下使用贪心是无法得到最优解的：

​ 硬币组合：[1,20,50]，总金额 𝑎𝑚𝑡=60 ，贪心算法只能找到 50+1×10 的兑换组合，共计 11 枚硬币，但动态规划可以找到最优解 20+20+20 ，仅需 3 枚硬币。

分析：

​ 对于组合1、3、4，需要金额6，那么按照贪心法：4+1+1三个，而3+3两个即可。

​ 如果硬币组合间有倍数关系，那么较大的硬币可以使用多个较小的硬币组合，意味着能用较小硬币的任意数量组合（加起来大于较大硬币），都可以直接使用较大硬币+一定数量的较小硬币替代去减少数量，不会出现3+3等于6，而4和3无法组合出6的这种情况。

贪心法案例-求最大子数组和图解

问题描述：

​ 给一个整数数组 ，请找出一个具有最大和的连续子数组（子数组最少包含一个元素），返回其最大和。

原始数组：

​ nums = [-2,1,-3,4,-1,2,1,-5,4]

蛮力法：

​ 直接遍历所有情况，将任意情况下的最优解记录下来，取最大的

 public static int solution(int[] data, int n) {
        if (n < 0 || (n == 1 && data[0] <= 0)) {
            return 0;
        }
        if (n == 1) {
            return data[0];
        }
        int maxSum = 0, thisSum;
        // 计算i到i,i到i+1,...,i到n的和，选出最大的一个子序列。  
        // 当i从0遍历到n-1时，则计算过了所有的子序列
        for (int i = 0; i < n; i++) {
            thisSum = 0;// i 表示子序列左侧的位置
            for (int j = i; j < n; j++) { // j 表示子序列右边的位置
                // 汇总 i到j 的所有数之和时，对比solution1发现
                // 其实每次求和不需要都从i位置开始，因为 i到k的和 = i到K-1的和 + data[k]
                thisSum += data[j];
                maxSum = Math.max(maxSum, thisSum);
            }
        }
        return maxSum;
    }

贪心法：

​ 如果当前的子序列和小于0，那么负数+任何数都会变小，所以应该舍弃掉当前已经选择的子序列。

​ 所以我们只需要考虑当前的最优解即可，不断向后遍历数组，直到遍历完数组就可以得到最大的子序列和。

1、初始化

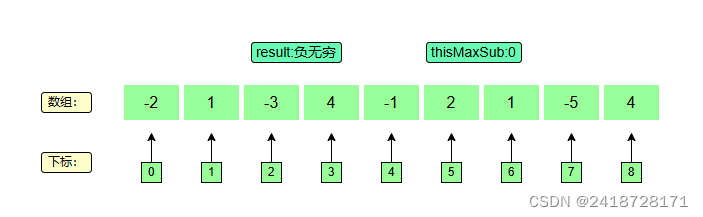
2、下标0

​ 下标为0，此时当前最大值变为$$0+(-2)=-2$$，然后结果取负无穷和-2之间较大的，即-2.

​ $$thisMaxSub=0+(-2)=-2$$

​ $$-2>负无穷推出result=-2$$

​ 因为-2为负数，一定会使后续的子序列和变小，直接舍弃。

​ $$-2<0推出thisMaxSub=0$$

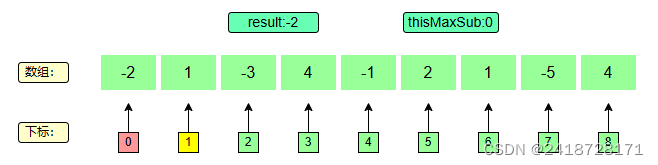
3、下标1

​ 当前最大值变为$$0+1=1$$，然后结果取-2和1之间较大的，即1.

​ $$thisMaxSub=0+1=1$$

​ $$1>-2推出result=1$$

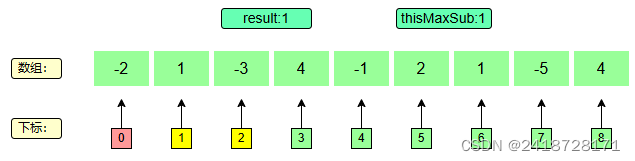
3、下标2

​ 当前最大值变为$$1+(-3)=-2$$，然后结果取1和-2之间较大的，即1.

​ $$thisMaxSub=1+(-3)=-2$$

​ $$1>-2推出result=1$$

​ 因为-2为负数，一定会使后续的子序列和变小，直接舍弃。

​ $$-2<0推出thisMaxSub=0$$

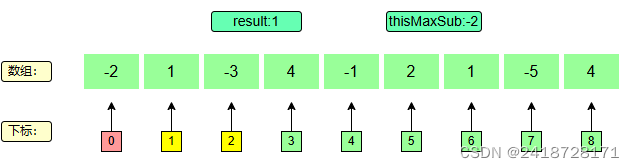
4、下标3

​ 当前最大值变为$$0+4=4$$，然后结果取1和4之间较大的，即4.

​ $$thisMaxSub=0+4=4$$

​ $$4>1推出result=4$$

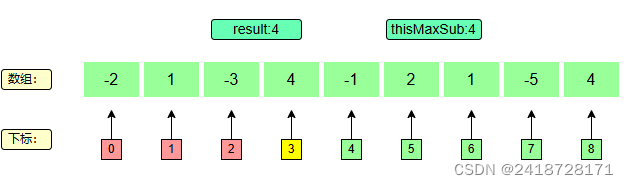
5、下标4

​ 当前最大值变为$$4+（-1）=3$$，然后结果取4和3之间较大的，即4.

​ $$thisMaxSub=4+（-1）=3$$

​ $$4>3推出result=4$$

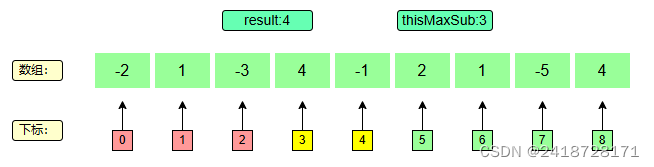
6、下标5

​ 当前最大值变为$$3+2=5$$，然后结果取4和5之间较大的，即5.

​ $$thisMaxSub=3+2=5$$

​ $$5>4推出result=5$$

…

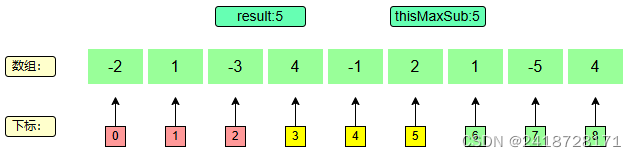
​ 最终得到最大值为6

    public static int execute(int[] data) {
        // result:存储最大值；thisMaxSub：存储当前最大值
        int result = Integer.MIN_VALUE, thisMaxSub = 0;
        for (int datum : data) {
            thisMaxSub += datum;
            result = Math.max(thisMaxSub, result);
            // tempMaxSub小于0的话，就可以直接舍弃掉，因为负数+任何数都会变得更小
            thisMaxSub = Math.max(thisMaxSub, 0);
        }
        return result;
    }