目录
整数对最小和
题目描述
注意
输出描述
示例1
输入
输出
说明
解析
答案
素数之积
题目描述
输入描述
输出描述
示例1
输入
输出
说明
示例2
输入
输出
说明
解析
找城市
题目描述
输入
输出
示例1
输入
输出
示例2
输入
输出
说明
解析
答案
整数对最小和
考察排序,数组拍平
题目描述
给定两个整数数组array1、array2,数组元素按升序排列。假设从array1、array2中分别取出一个元素可构成一对元素,
现在需要取出k对元素,并对取出的所有元素求和,计算和的最小值
注意
两对元素如果对应于array1、array2中的两个下标均相同,则视为同一对元素。
输入描述
输入两行数组array1、array2,每行首个数字为数组大小size(0 < size <= 100);
0 < array1[i] <= 1000
0 < array2[i] <= 1000
接下来一行为正整数k
0 < k <= array1.size() * array2.size()
输出描述
满足要求的最小和
示例1
输入
1 1 2 3
1 2 3 3
2
输出
4
说明
用例中,需要取2对元素
取第一个数组第0个元素与第二个数组第0个元素组成1对元素[1,1];
取第一个数组第1个元素与第二个数组第0个元素组成1对元素[1,1];
求和为1+1+1+1=4,为满足要求的最小和
解析
新建一个二维数组,数组的行列长度和array1、array2的长度对应,通过循环给数组的每一位赋值,
arr[i][j]表示的为一对元素的和,将二维数组拍平,然后按升序排列,取前k位的和即为满足要求的最小和。
答案
function calcPairSum(str){
let arr = str.split('\n')
let n = Number(arr.pop())
let [array1,array2]=arr.map(v=>v.split(' ').map(Number))
let len1 = array1.length;
let len2 = array2.length
arr = new Array(len1).fill(0).map(v=>new Array(len2).fill(0))
for(let i = 0;i<len1;i++){
for(let j = 0;j<len2;j++){
arr[i][j]=array1[i]+array2[j]
}
}
arr=arr.flat().sort((a,b)=>a-b)
return arr.slice(0,n).reduce((t,v,i)=>t+v)
}
console.log(calcPairSum(`1 1 2 3
1 2 3 3
2`))素数之积
考察数学素数定义
题目描述
RSA加密算法在网络安全世界中无处不在,它利用了极大整数因数分解的困难度,数据越大,安全系数越高,给定一个32位正整
数,请对其进行因数分解,找出是哪两个素数的乘积。
输入描述
一个正整数num
0<num <= 2147483647
输出描述
如果成功找到,以单个空格分割,从小到大输出两个素数,分解失败,请输出-1-1
示例1
输入
15
输出
35
说明
因数分解后,找到两个素数3和5,使得3*5=15,按从小到大排列后,输出3 5
示例2
输入
27
输出
-1-1
说明
通过因数分解,找不到任何索数,使得他们的乘积为27,输出-1-1
解析
function resolvePrimeNumber(n){
for(let i=2;i<=n**0.5;i++){
if(n%i===0){
let tmp = n/i
if(isPrime(tmp)&&isPrime(i)){
return [tmp,i].sort((a,b)=>a-b).join(' ')
}
}
}
return '-1 -1'
}
function isPrime(n){
for(let i=2;i<=n**0.5;i++){
if(n%i===0){
return false
}
}
return true
}
console.log(resolvePrimeNumber(15))
console.log(resolvePrimeNumber(27))找城市
考察深度遍历,递归,数组去重,字符串分割。
题目描述
一张地图上有n个城市,城市和城市之间有且只有一条道路相连:要么直接相连,要么通过其它城市中转相连(可中转一次或多次)。
城市与城市之间的道路都不会成环。 当切断通往某个城市 i 的所有道路后,地图上将分为多个连通的城市群,设该城市i的聚集度为DPi
(Degree of Polymerization), DPi = max(城市群1的城市个数, 城市群2的城市个数, … 城市群m的城市个数)。
请找出地图上 DP 值最小的城市(即找到城市 j,使得 DPj = min(DP1, DP2 … DPn) )
提示:如果有多个城市都满足条件,这些城市都要找出来(可能存在多个解)。
提示:DPi的计算,可以理解为已知一棵树,删除某个节点后,生成的多个子树,求解多个子树节点数的问题。
输入
每个样例:第一行有一个整数N,表示有N个节点。1<=N<=1000
接下来的N-1行每行有两个整数x,y,表示城市x与城市y连接。1<=x, y<=N
输出
输出城市的编号。如果有多个,按照编号升序输出。
示例1
输入
5
1 2
2 3
3 4
4 5
输出
3
示例2
输入
6
1 2
2 3
2 4
4 5
4 6
输出
2 4
说明
当切断通往城市3的所有道路后,1,2为一个城市群,4,5为一个城市群,DPi为2,此时DPi为其它Dpi中最小的,所以为城市3
解析
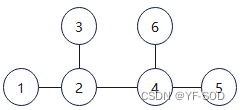
通过深度遍历,每次遍历一个元素就将该元素加入一个数组,遍历完后再将这个元素加入一遍,这样我们通过该元素分割时就可以拿到切断该元素后的相连的节点。
例如上图(示例2),我们通过上面遍历方法得出的数组为[1,2,3,2,4,5,4,6,4,2,1]。然后我们将这个数组形成一个环,这样对每个数进行切割后得到的数组内去重后就是一个城市群,例如对2进行切割,可以拿到[1],[3],[4,5,4,6,4],[1]然后由于是环,所以第一个和最后一个是一组,最后去重后就是分组结果[1][3][4,5,6],所以可以得到DPi为3即取[4,5,6]。
答案
function getDP(str) {
let arr = str.split('\n')
let n = arr.shift()
let obj = {}
arr.forEach(v => {
v = v.split(' ')
if (!obj[v[0]]) {
obj[v[0]] = { value: v[0], next: [] }
}
if (!obj[v[1]]) {
obj[v[1]] = { value: v[1], next: [] }
}
obj[v[0]].next.push(obj[v[1]])
obj[v[1]].next.push(obj[v[0]])
})
let start = Object.values(obj).filter(v => v.next.length === 1)[0]
let pathArr = dfs(start)
let pathStr = pathArr.join(' ')
let citys = uni(pathArr)
let dp = Infinity
let dpCitys = []
for (let i = 0; i < n; i++) {
let cur = citys[i]
let tmp = pathStr.split(cur).map(v => v.split(' '))
//第一个节点和最后一个节点合成一个
tmp[0] = tmp[0].concat(tmp.pop())
let dpi = 1
tmp.forEach(v => {
let tmpDpi = uni(v.filter(city => city !== '')).length
if (tmpDpi > dpi) {
dpi = tmpDpi
}
})
if (dpi < dp) {
dpCitys = [cur]
dp = dpi
} else if (dpi === dp) {
dpCitys.push(cur)
}
}
return dpCitys.sort((a, b) => a - b).join(' ')
}
function uni(arr) {
return [...new Set(arr)]
}
function dfs(start, set = new Set(), res = []) {
res.push(start.value)
set.add(start)
let next = start.next.filter(v => !set.has(v))
next.forEach((v, i) => {
dfs(v, set, res)
// 每次遍历一个元素就将该元素加入一个数组,遍历完后再将这个元素加入一遍,
// 这样我们通过该元素分割时就可以拿到切断该元素后的相连的节点。
res.push(start.value)
})
return res
}
console.log(getDP(`5
1 2
2 3
3 4
4 5`))
console.log(getDP(`6
1 2
2 3
2 4
4 5
4 6
`))