承接上文:2023年第十四届蓝桥杯JavaB组省赛真题及全部解析(下)。
目录
七、试题 G:买二赠一
八、试题 H:合并石子
九、试题 I:最大开支
十、试题 J:魔法阵
题目来自:蓝桥杯官网
七、试题 G:买二赠一

• 题目分析:
因为每次我们要尽可能的使免费拿走商品的价格尽可能的大,但是免费的金额又与较便宜的物品有关,这是一道贪心题(猜的,比赛想到就可以写了,贪心的证明是非常恶心的)。
• 解题思路:
1. 排序商品价格(降序)。
2. 使用队列来存储免费的金额。
3. 遍历全部商品,遇到能免费的商品(小于队列队头元素),出队列,这个商品跳过(不加到总和)。其他的正常遍历,加到总和。
4. 一旦选了两个商品,将后面选的(肯定小于前面选的)一半价格加入队列。
5. 返回结果。
如果下面的排序写法看不懂的话,可以去看我之前写的Java sort 详解,里面都有写到。
• 代码编写:
import java.util.*;
public class Main{
public static void main(String[] args) {
Scanner in = new Scanner(System.in);
int n = in.nextInt();
//读入数据
Integer[] arr = new Integer[n];
for(int i = 0;i < n;i++){
arr[i] = in.nextInt();
}
Arrays.sort(arr,(o1,o2) -> {//从大到小排序
return o1 >= o2 ? -1 : 1;//或者(o2 - o1)
});
long sum = 0;//存储总花费
Queue<Integer> q = new LinkedList<>();//存储可以免费的金额,保证是先进先出
int count = 0;//记录何时到达二次
for(int i = 0;i < n;i++){
if(!q.isEmpty() && q.peek() >= arr[i]) {//说明可以免费带走
q.poll();//队头免费金额用过了,把队头弹出去。
continue;//跳过这个商品
}
sum += arr[i];
count++;
if(count == 2){
count = 0;
q.add(arr[i] / 2);//可以免费的金额,存入队列
}
}
System.out.println(sum);
}
}• 运行结果:
八、试题 H:合并石子

• 题目分析:
这是一道区间 dp 的问题,关于区间 dp 可能平时会遇到的比较少。如果不了解的话,建议先去看看区间 dp,再去洛谷把 合并石子 (这道题的简化版)做了。
• 解题思路:
1. 状态表示:
dp[i][j][k]:表示合并区间[i , j]为 1 堆,且颜色为 k 的最小花费。
其他的参数说明:
sum[i]:表示前 i 堆石头的和(前缀和方便后续求值)。
cost[ij][j]:表示从在区间[ i ,j ]的最小花费(dp表示的是 1 堆,最后结果不一定为 1 堆,所以要重新创建一个)。
nums[i][j]:表示在区间[ i ,j ]的最小堆数。
2. 状态转移方程:
dp[i][j][(k + 1) % 3] 可以由分割点 j 的左边花费数 + 分割点 j 的右边花费数 + 合并两堆的花费数,转移过来。
dp[i][end][(k + 1) % 3] = Math.min(dp[i][end][(k + 1) % 3],dp[i][j][k] + dp[j + 1][end][k] + sum[end] - sum[i - 1]);3.初始化:
把dp[ i ][ i ][col[ i ] ]初始为0,因为这本来就是 1 堆,不用合并花费。
其他的代码里面都有注释就不多赘述了。
• 代码编写:
import java.util.*;
public class Main {
static int INF = 0x3f3f3f3f;
public static void main(String[] args) {
Scanner in = new Scanner(System.in);
int n = in.nextInt();
int[] col = new int[n + 1];//存储颜色
int[] sum = new int[n + 1];//前缀和
int[][] cost = new int[n + 1][n + 1];//表示i 到 j 区间的花费
int[][] nums = new int[n + 1][n + 1];//区间的堆数
//读入数据
for(int i = 1;i <= n;i++){
sum[i] = sum[i - 1] + in.nextInt();
}
for(int i = 1;i <= n;i++){
col[i] = in.nextInt();
}
//初始化
int[][][] dp = new int[n + 1][n + 1][3];
for(int i = 1;i <= n;i++){
for(int j = 1;j <= n;j++){
nums[i][j] = j - i + 1;//独自成一堆
Arrays.fill(dp[i][j],INF);//求最小值,防止被 0 干预
}
dp[i][i][col[i]] = 0;//只有自己且颜色存在
}
//填写 dp 表
for(int len = 1;len <= n;len++){//枚举长度
for(int i = 1;i + len - 1 <= n;i++){//枚举起点
int end = i + len - 1;//找到终点
for(int k = 0;k < 3;k++){//枚举颜色
for(int j = i;j < end;j++){//枚举分割点
if(dp[i][j][k] != INF && dp[j + 1][end][k] != INF){//去掉不存在的节点
dp[i][end][(k + 1) % 3] = Math.min(dp[i][end][(k + 1) % 3],dp[i][j][k] + dp[j + 1][end][k] + sum[end] - sum[i - 1]);
nums[i][end] = 1;//注意我们的状态就是表示合成一堆
}
}
}
}
}
//将堆数为 1 的花费填入 cost(只能填 1 )
for(int i = 1;i <= n;i++){
for(int j = i;j <= n;j++){
if(nums[i][j] == 1){
cost[i][j] = Math.min(dp[i][j][0],Math.min(dp[i][j][1],dp[i][j][2]));
}
}
}
//dp 表示是合成 1 堆,但是最后不一定能合成一堆,所以要再查找一次。
//把所有区间都枚举出来,找到最小堆数的最小花费
for(int k = 1;k <= n;k++){
for(int i = 1;i <= k;i++){
for(int j = k + 1;j <= n;j++){
if(nums[i][j] > nums[i][k] + nums[k + 1][j]){
nums[i][j] = nums[i][k] + nums[k + 1][j];
cost[i][j] = cost[i][k] + cost[k + 1][j];
}else if(nums[i][j] == nums[i][k] + nums[k + 1][j]){
cost[i][j] = Math.min(cost[i][j],cost[i][k] + cost[k + 1][j]);
}
}
}
}
System.out.println(nums[1][n] + " " + cost[1][n]);
}
}• 运行结果:

九、试题 I:最大开支

• 题目分析:
这题不能使用动态规划来做,因为时间复杂度至少为O(n^2),题目给出的数据为 10 ^ 5,会超时的,所以我们要另找方法。
考虑到H函数在乘于人数后,会变成一个一元二次方程 k * x ^ 2 + bx(k为负数);,开口向下,先递增后递减,并且递增的速度越来越慢,也就是说,随着项目参与人数的增加,总花费的增加(后一个减去前一个)会变得越来越少。因此我们贪心的点就来了,在往项目中增加人数时,我们每次都选取花费增加最多的项目添加。由局部最优,带来全局最优。
• 解题思路:
先算出一个花费增加数的公式:
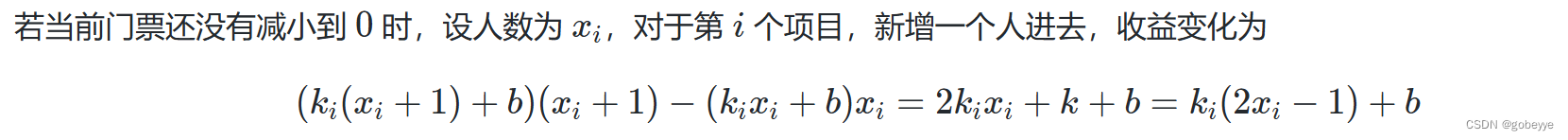
我们配合优先级队列就能达到O(n * log(n))的时间复杂度。
• 代码编写:
import java.util.*;
public class Main{
static long sum = 0;//最初最终的总和
static int[] k;
static int[] b;
static int[] cnt;//记录对应项目的人数
static class Pair{//不能使用Java自带的,会遍历错误,很奇怪
int key;//表示可以直接加到总和的花费
int val;//表示第 val 个项目
public Pair(int key,int val){
this.key = key;
this.val = val;
}
}
public static void main(String[] args) {
Scanner in = new Scanner(System.in);
int n = in.nextInt(),m = in.nextInt();
k = new int[m + 1];
b = new int[m + 1];
cnt = new int[m + 1];
//大根堆
PriorityQueue<Pair> q = new PriorityQueue<>((o1,o2) -> {
return o1.key > o2.key ? -1 : 1;
});
//读入数据
for(int i = 1;i <= m;i++){
k[i] = in.nextInt();
b[i] = in.nextInt();
cnt[i] = 1;
q.add(new Pair(mul(cnt[i],i),i));
}
for(int i = 0;i < n;i++){
Pair tmp = q.poll();
if(tmp.key <= 0){//小于0说明后续都小于0,直接退出即可
break;
}
sum += tmp.key;
Integer t = tmp.val;
q.add(new Pair((k[t] * (2 * cnt[t] + 1) + b[t]),t));//推导出来的公式。
cnt[t]++;//对应的人数 + 1
}
System.out.println(sum);
}
public static int mul(int x,int i){
return (k[i] * x + b[i]) * x;//题目给出的公式
}
}
• 运行结果:
十、试题 J:魔法阵

• 解题思路:
利用动态规划 + Dijkstra 算法的一些思想来做。
1. 状态表示:
dp[i][j]:表示从节点 0 到节点 i ,使用魔法消除最后 j 条边的最小总伤害。
2. 状态转移方程:
下面都是以 i 为终点,u 为起点来推的,w 为 u -> i 的权值。
• 不使用魔法:dp[i][0] = min(dp[i][0] , dp[u][0] + w);
• 使用魔法:dp[i][j] = min(dp[u][j - 1],dp[i][j]);其中 1<= j <= k。
• 魔法使用过了:dp[i][k] = min(dp[i][k] , dp[u][k] + w);
3. 初始化:
dp表除了 [0][0] 初始化为 0 ,其它的初始化为无穷大。
4. 填表:
配合 Dijkstra 算法进行填表。
5. 返回值:
返回 dp[n - 1][k]即可。
剩下的一些零碎在代码中都有注释。
• 代码编写:
import java.util.*;
public class Main {
static class Pair<K,V>{//不能使用 Java 自带的,会编译不过去
K v;
V w;
public Pair(K v,V w){
this.v = v;
this.w = w;
}
}
public static void main(String[] args) {
Scanner in = new Scanner(System.in);
int n = in.nextInt(),k = in.nextInt(),m = in.nextInt();
int INF = 0x3f3f3f3f;
List<List<Pair<Integer,Integer>>> ret = new ArrayList<>();//使用邻接表的方式存储边
for(int i = 0;i < n;i++){
ret.add(new ArrayList<>());
}
//1.创建 dp 表
int[][] dp = new int[n][k + 1];
for(int i = 0;i < n;i++){
Arrays.fill(dp[i],INF);
}
//2.初始化
dp[0][0] = 0;
for(int i = 0;i < m;i++){
int u = in.nextInt(),v = in.nextInt(),w = in.nextInt();
ret.get(u).add(new Pair<>(v,w));
ret.get(v).add(new Pair<>(u,w));//无向图,所以两边都要存储边
}
//3.填表
Queue<Integer> q = new LinkedList<>();//用来存放起点
q.add(0);
while(!q.isEmpty()){
int u = q.poll();
for(Pair<Integer,Integer> pair:ret.get(u)){//取出边
// 下面是 Dijkstra 算法的思路(不是完全一样)
int v = pair.v;
int w = pair.w;
boolean flag = false;//表示还有没有从 v 节点为起点的必要,
// 如果为 false 的话说明以 v 为起点绝对不是最小路径,要舍去,同时还可以防止死循环
if(dp[v][0] > dp[u][0] + w){//选取最优
flag = true;
dp[v][0] = dp[u][0] + w;
}
for(int j = 1;j <= k;j++){
if(dp[v][j] > dp[u][j - 1]){
flag = true;
dp[v][j] = dp[u][j - 1];
}
}
if(dp[v][k] > dp[u][k] + w){
flag = true;
dp[v][k] = dp[u][k] + w;
}
if(flag == true){
q.add(v);
}
}
}
//4.返回值
// System.out.println(Math.min(dp[n - 1][0],dp[n - 1][k]));
System.out.println(dp[n - 1][k]);//都行
}
}• 运行结果:
结语:
其实写博客不仅仅是为了教大家,同时这也有利于我巩固知识点,和做一个学习的总结,由于作者水平有限,对文章有任何问题还请指出,非常感谢。如果大家有所收获的话还请不要吝啬你们的点赞收藏和关注,这可以激励我写出更加优秀的文章。







![Detailed Steps for Troubleshooting ORA-00600 [kdsgrp1] (文档 ID 1492150.1)](https://img-blog.csdnimg.cn/img_convert/a9724249e242b12aae6ec3ee13792cda.png)