CV炼丹师勇闯力扣训练营
代码随想录算法训练营第13天
二叉树的递归遍历
二叉树的迭代遍历、统一迭代
二叉树的层序遍历
一、二叉树的递归遍历(深度优先搜索)
【递归步骤】
1.确定递归函数的参数和返回值:确定哪些参数是递归的过程中需要处理的,那么就在递归函数里加上这个参数, 并且还要明确每次递归的返回值是什么进而确定递归函数的返回类型。
2.确定终止条件: 写完了递归算法, 运行的时候,经常会遇到栈溢出的错误,就是没写终止条件或者终止条件写的不对,操作系统也是用一个栈的结构来保存每一层递归的信息,如果递归没有终止,操作系统的内存栈必然就会溢出。
3.确定单层递归的逻辑: 确定每一层递归需要处理的信息。在这里也就会重复调用自己来实现递归的过程
代码如下(Python):二叉树的前/中/后序遍历
from typing import List
# Definition for a binary tree node.
class TreeNode:
def __init__(self, val=0, left=None, right=None):
self.val = val
self.left = left
self.right = right
# 前序遍历-递归-LC144_二叉树的前序遍历
class Solution:
def preorderTraversal(self, root: TreeNode) -> List[int]:
res = []
def dfs(node):
if node is None:
return
res.append(node.val)
dfs(node.left)
dfs(node.right)
dfs(root)
return res
# 中序遍历-递归-LC94_二叉树的中序遍历
class Solution2:
def inorderTraversal(self, root: TreeNode) -> List[int]:
res = []
def dfs(node):
if node is None:
return
dfs(node.left)
res.append(node.val)
dfs(node.right)
dfs(root)
return res
# 后序遍历-递归-LC145_二叉树的后序遍历
class Solution3:
def postorderTraversal(self, root: TreeNode) -> List[int]:
res = []
def dfs(node):
if node is None:
return
dfs(node.left)
dfs(node.right)
res.append(node.val)
dfs(root)
return res
""" [1,2,4,5,3]
1
/ \
2 3
/ \
4 5
"""
# 创建二叉树
root = TreeNode(1)
root.left = TreeNode(2)
root.right = TreeNode(3)
root.left.left = TreeNode(4)
root.left.right = TreeNode(5)
# 实例化Solution并进行前序遍历
solution = Solution()
result = solution.preorderTraversal(root)
# 打印前序遍历的结果
print(result)
二、二叉树的迭代遍历
三、二叉树的统一迭代
# Todo
四、二叉树的层序遍历(广度优先搜索)
层序遍历一个二叉树。就是从左到右一层一层的去遍历二叉树。这种遍历的方式和我们之前讲过的都不太一样。
需要借用一个辅助数据结构即队列来实现,队列先进先出,符合一层一层遍历的逻辑,而用栈先进后出适合模拟深度优先遍历也就是递归的逻辑。
而这种层序遍历方式就是图论中的广度优先遍历,只不过我们应用在二叉树上。

从左到右遍历层序遍历二叉树动画如图:
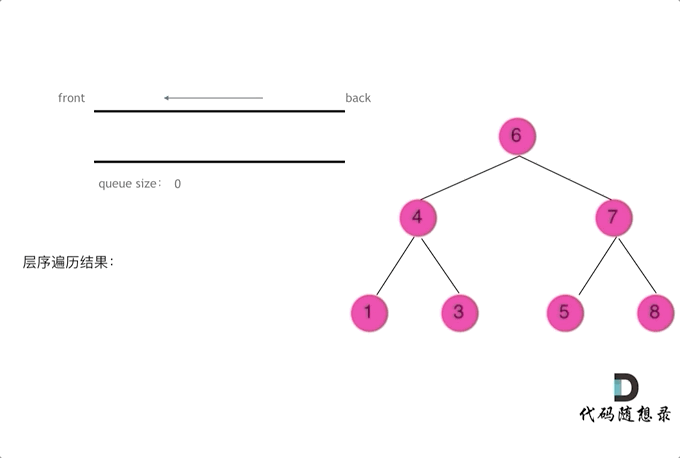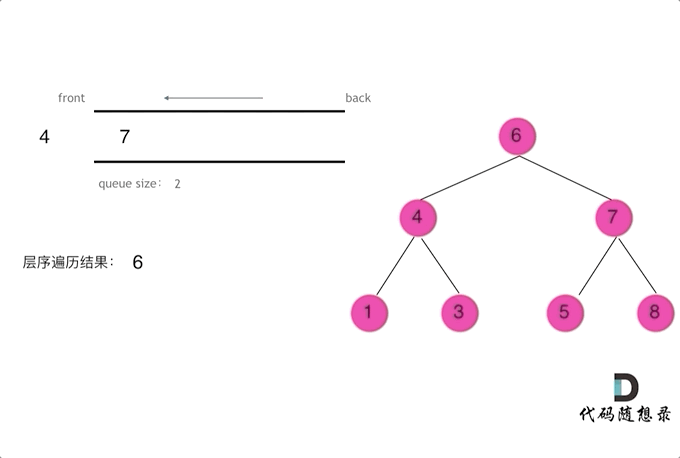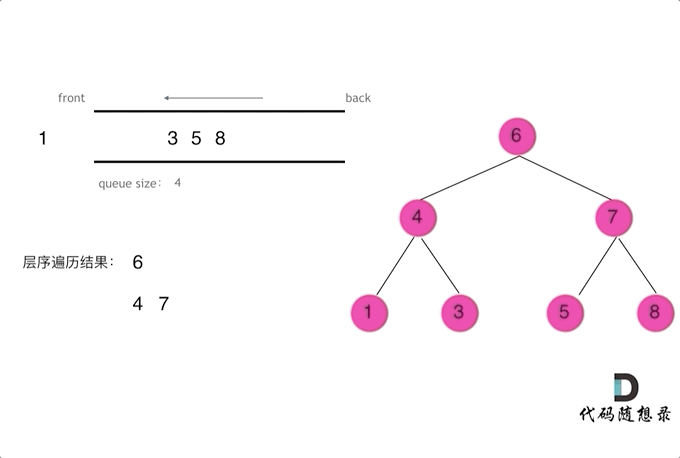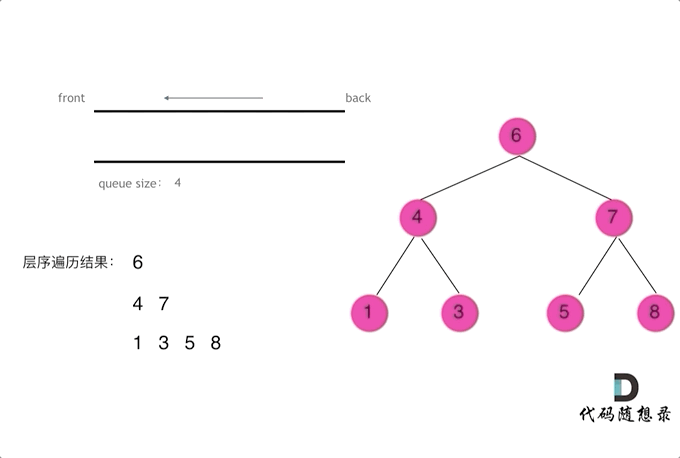
代码如下(Python)
"""
利用长度法
"""
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:
def levelOrder(self, root: Optional[TreeNode]) -> List[List[int]]:
if not root:
return []
queue = collections.deque([root])
result = []
while queue:
level = []
for _ in range(len(queue)):
cur = queue.popleft()
level.append(cur.val)
if cur.left:
queue.append(cur.left)
if cur.right:
queue.append(cur.right)
result.append(level)
return result
"""
递归法
"""
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:
def levelOrder(self, root: Optional[TreeNode]) -> List[List[int]]:
if not root:
return []
levels = []
def traverse(node, level):
if not node:
return
if len(levels) == level:
levels.append([])
levels[level].append(node.val)
traverse(node.left, level + 1)
traverse(node.right, level + 1)
traverse(root, 0)
return levels
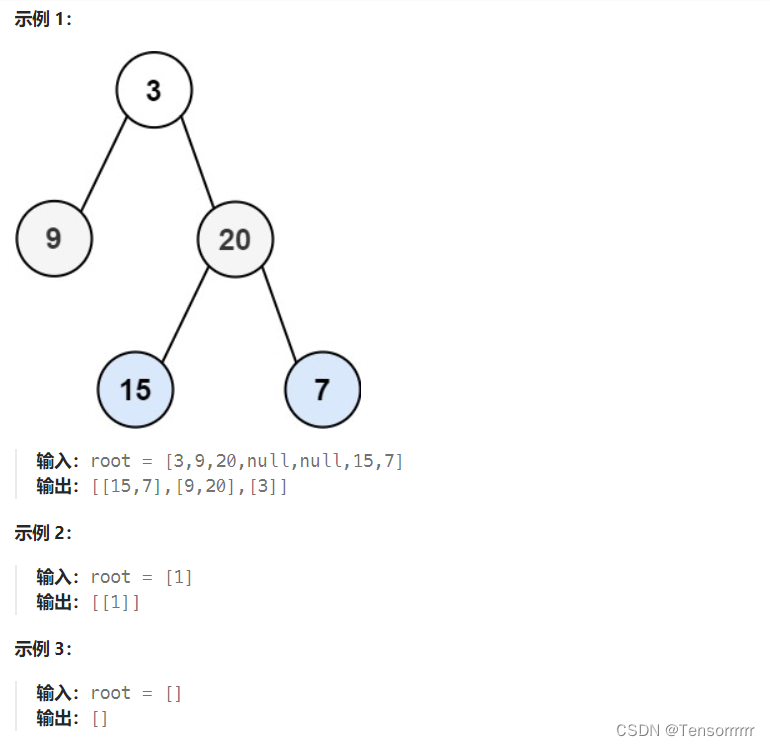
107.二叉树的层次遍历 II
给你二叉树的根节点 root ,返回其节点值 自底向上的层序遍历 。 (即按从叶子节点所在层到根节点所在的层,逐层从左向右遍历)
class TreeNode:
def __init__(self, val=0, left=None, right=None):
self.val = val
self.left = left
self.right = right
class Solution:
def levelOrderBottom(self, root: TreeNode) -> List[List[int]]:
if not root:
return []
queue = collections.deque([root])
result = []
while queue:
level = []
for _ in range(len(queue)):
cur = queue.popleft()
level.append(cur.val)
if cur.left:
queue.append(cur.left)
if cur.right:
queue.append(cur.right)
result.append(level)
return result[::-1]
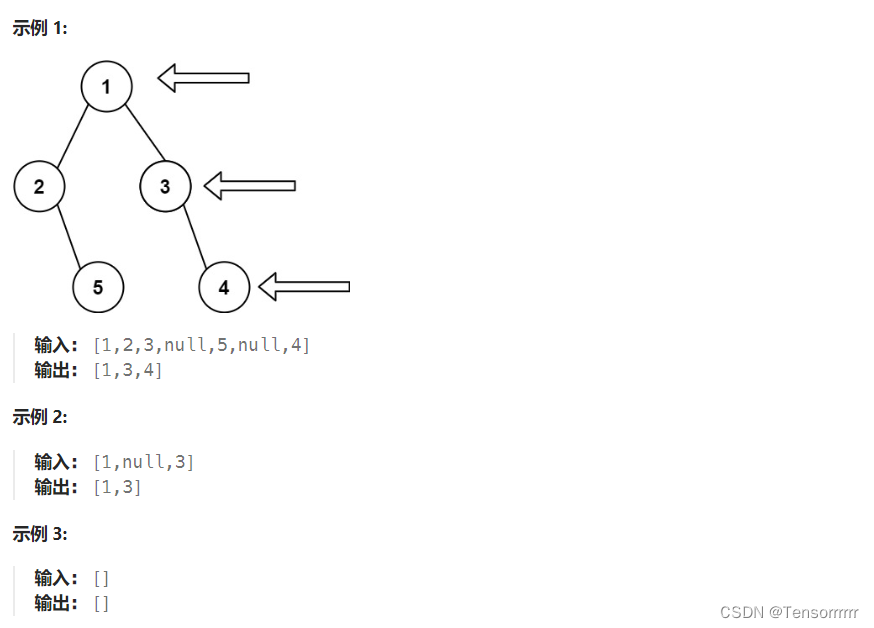
199. 二叉树的右视图
给定一个二叉树的 根节点 root,想象自己站在它的右侧,按照从顶部到底部的顺序,返回从右侧所能看到的节点值。
class Solution:
def rightSideView(self, root: TreeNode) -> List[int]:
if not root:
return []
q = collections.deque([root])
right_view = []
while q:
level_size = len(q)
for i in range(len(q)):
node = q.popleft()
if i == level_size - 1:
right_view.append(node.val)
if node.left:
q.append(node.left)
if node.right:
q.append(node.right)
return right_view
637.二叉树的层平均值
给定一个非空二叉树的根节点 root , 以数组的形式返回每一层节点的平均值。与实际答案相差 10^(-5) 以内的答案可以被接受。