本文引用董晓算法的部分图片。

一些不能带入纸质资料的竞赛，网络流纳入考纲。

因为需要默写，想来也不会考默写dinic这种算法难倒大家，只需要快速敲对EK算法就行了。

EK算法能在O(n*m^2)的复杂度内解决最大流问题，其中最大流就是源点到汇点的最大流量。

一般来说起点的流量是无穷，每条边有一个最大流容量c，再定义当前边已经流过了容量f。

很显然，网络流模型必须满足每条边的f<=c，同时每条边的流入量必须等于流出量。

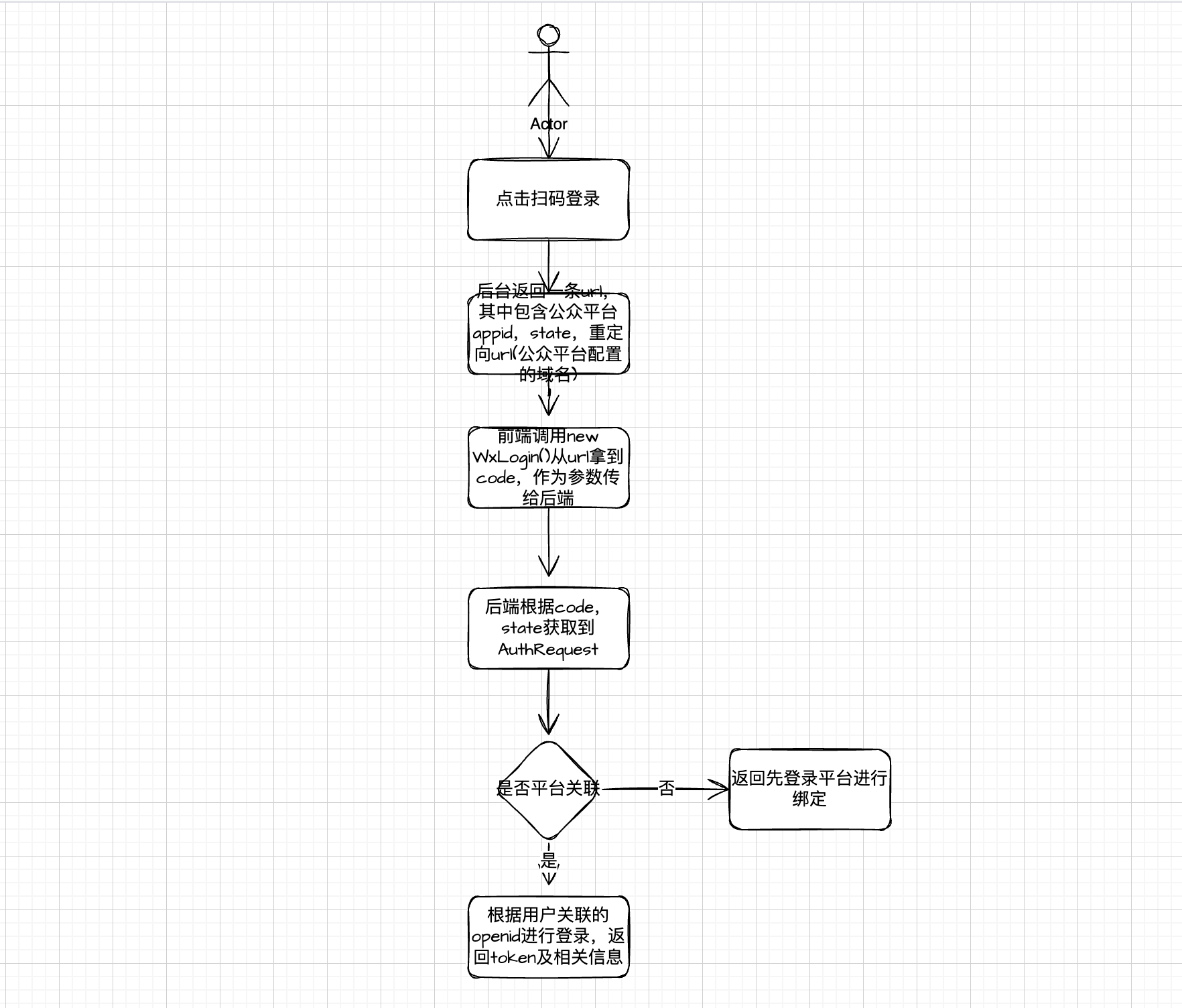
EK算法的过程如下：

不断尝试，从源点找一条到达汇点流量大于0的路径，我们又称这条路为增广路。

如图就是一条增广路。（图中5/5表示f/c）

但是确定一条增广路后，我们找新的增广路，就会因为旧的路径已经存在而被阻挡。

这时候我们就需要建立反向边。

反向边的意义在于给了之前存在的路径一个反悔的机会。

如图所示，假设右下角是汇点，左图是一条黑色的增广路，中间图片中，新增了一条红色的增广路，因为建立了反向边，所以红色路径可以正常到达汇点。等效成右图所示的结果，这样最大流就从5变成10了，其实就是通过反向边来达到旧边给新边让路的效果。

代码如下所示：

#include<bits/stdc++.h>
using namespace std;
const int INF=0x3f3f3f3f;
const int N=1e3+5;
int a[N][N];
int mf[N],isque[N];
//mf表示到该点的流量 
int pre[N];
int n,m,e;
int bfs(int su,int sv){
	memset(mf,0,sizeof(mf));
	for (int i=0;i<=n+m+1;i++) mf[i]=0;
	for (int i=0;i<=n+m+1;i++) isque[i]=0;
	mf[su]=INF;
	queue<int> q;
	q.push(su);
	isque[su]=true;
	pre[su]=-1;
	while(!q.empty()){
		int u=q.front();
		q.pop();
		isque[u]=false;
		for (int v=0;v<=n+m+1;v++){
			if (u==v) continue;
			if (mf[v]<min(mf[u],a[u][v])){
				mf[v]=min(mf[u],a[u][v]);
				pre[v]=u;
				if (mf[sv]!=0)	return true;
				if (isque[v]==false){
					q.push(v);
					isque[v]=true;
				}
			}
		}
	}
	return false;
}
int ek(int su,int sv){
	int ans=0;
	while(bfs(su,sv)){
		ans+=mf[sv];
		int p=sv;
		while(pre[p]!=-1){
			a[p][pre[p]]+=mf[sv];
			a[pre[p]][p]-=mf[sv];
			p=pre[p];
		}
	}
	return ans;
}
void work(){
	cin>>n>>m>>e;
	for (int i=1;i<=n;i++){
		a[0][i]=1;
		a[i][0]=0;
	}
	for (int i=1;i<=m;i++){
		a[i+n][n+m+1]=1;
		a[n+m+1][i+n]=0;
	}
	for (int i=1;i<=e;i++){
		int u,v;cin>>u>>v;
		a[u][v+n]=1;
		a[v+n][u]=0;
	}
	cout<<ek(0,n+m+1)<<"\n";
}
signed main(){
	ios::sync_with_stdio(false);cin.tie(0);cout.tie(0);
	work();
	return 0;
} 

其中用到了一个BFS和一个DFS（ek）。

BFS在不断找增广路（从源点找一条到达汇点流量大于0的路径），DFS把找到的增广路的流量确定下来，表示到边上，减少对应的容量，并给反向边增加相同的容量（能过去多少就能反悔多少）。

图的存储用邻接矩阵表示（反正都用EK算法了qwq，就更简单一点吧）。

BFS不断找增广路，其中套了一个SPFA的队列优化。mf数组表示到该点的流量为多少，因为需要不断找增广路，并把增广路得到的路径确定到边权的f（已经流过了容量），所以每次确定完成后mf数组就不再需要了，所以每次开始BFS之前要重新置为0。

其中有这个代码:

if (mf[v]<min(mf[u],a[u][v])){
    mf[v]=min(mf[u],a[u][v]);
}

mf[u]表示前面的点u最多给后面的点v多少流量，a[u][v]邻接矩阵表示这个管子最多承受多少流量，两者的较小值才是v点能过去的最大流量（此处贪心的想，因为要求最大流，所以肯定v点流量越大越好）

这里可能会有一个比较疑惑的点，那既然u到达了v，mf[v]更新了流量，为了满足每条边的流入量必须等于流出量，u点的mf数组不是应该更新吗？为什么代码里没有更新。如果不更新的话，假如mf[u]=5,岂不是u的每一个mf[v]都会被设置成5？

这是因为BFS的意义是找到一条可行的增广路，而不是真的全部遍历完才把结果抛给DFS。这样一旦有一条路径到达汇点，就一定仅仅只会有一条路径（感觉说了句废话），不会出现重复的情况。

这里可以发现mf的意义不是当前点的实际最大流，而是为了找到一条尽可能大且可行的流服务的。

感谢观看！