美团校招机试 - 小美的平衡矩阵（20240309-T1）

题目来源

美团校招笔试真题_小美的平衡矩阵

题目描述

小美拿到了一个 n * n 的矩阵，其中每个元素是 0 或者 1。

小美认为一个矩形区域是完美的，当且仅当该区域内 0 的数量恰好等于 1 的数量。

现在，小美希望你回答有多少个 i * i 的完美矩形区域。你需要回答 1 ≤ i ≤ n 的所有答案。

输入描述

第一行输入一个正整数 n，代表矩阵大小。

1 ≤ n ≤ 200

接下来的 n 行，每行输入一个长度为 n 的 01 串，用来表示矩阵。

输出描述

输出 n 行，第 i 行输出的 i * i 的完美矩形区域的数量。

用例

输入	4 1010 0101 1100 0011
输出	0 7 0 1
说明	无

题目解析

本题需要我们求解 i * i 的完美矩形区域的数量，i 取值 1~n.

完美矩形区域：当且仅当该区域内 0 的数量恰好等于 1 的数量

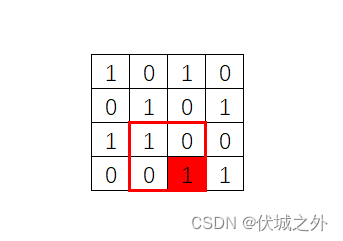
比如下图中黄色部分是一个 2x2 的矩形区域，其中01数量相等，因此是一个完美矩形区域

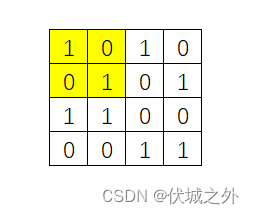
因此，本题的关键其实是，求解输入矩阵中，任意 i * i 正方形区域中 '1' 的数量oneCount，如果满足： oneCount * 2 == i * i，则对应正方形区域是完美的。

那么，如何求解输入矩阵中，任意正方形区域中 '1' 的数量呢？

我们可以基于“二维数组前缀和”的知识来求解。

假设 dp[i][j] 表示输入矩阵中以 (0,0)为左上角点，(i,j)为右下角点的矩形中 '1' 的数量。

比如上图中，dp[1][1] = 2，即以(0,0)为左上角点，(1,1)为左下角点的矩形中 '1' 的数量为 2。

下图中红色区域1的数量存在关系如下：

其中橙色区域是绿色和蓝色区域的重叠区域，为了避免重复计算，所以要减去。

即存在状态转移方程如下：

dp[i][j] = dp[i][j-1] + dp[i-1][j] - dp[i-1][j-1] + (matrix[i][j] == '1' ? 1 : 0)

上面状态转移方程求解i=0, j=0的右下角位置矩形时，会发生越界异常，

因此我们定义dp二维数组时，需要将dp矩阵的行数、列数都定义为n+1。dp矩阵的第一行和第一列初始为0。

之后，我们就可以遍历dp中所有正方形，然后基于dp来求解正方形中1的数量。比如下图中：

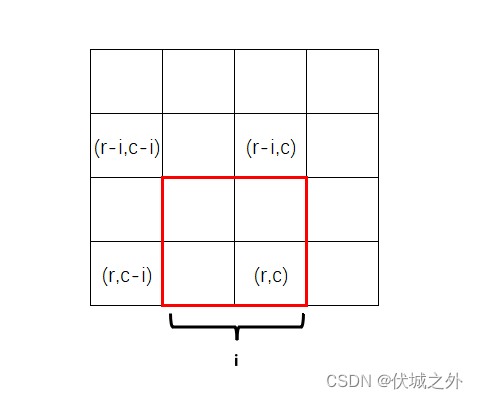
我们要求解：边长为 i=2，右下角位置 (r=3, c=2) 的正方形中 '1' 的数量，则有公式如下：

dp[r][c] - dp[r][c - i] - dp[r - i][c] + dp[r - i][c - i]

公式可以对照下图理解：

JS(Node)算法源码

const rl = require("readline").createInterface({ input: process.stdin });
var iter = rl[Symbol.asyncIterator]();
const readline = async () => (await iter.next()).value;

void (async function () {
  const n = parseInt(await readline());

  const matrix = [];
  for (let i = 0; i < n; i++) {
    matrix.push(await readline());
  }

  // 二维数组前缀和
  // dp[i][j] 表示matrix矩阵中以 (i-1, j-1) 位置为右下角点的矩形中1的数量
  const dp = new Array(n + 1).fill(0).map(() => new Array(n + 1).fill(0));
  for (let i = 1; i <= n; i++) {
    for (let j = 1; j <= n; j++) {
      // 此处公式请看图示说明
      dp[i][j] =
        parseInt(matrix[i - 1][j - 1]) +
        dp[i - 1][j] +
        dp[i][j - 1] -
        dp[i - 1][j - 1];
    }
  }

  // i 表示正方形边长
  for (let i = 2; i <= n; i += 2) {
    // i 为奇数时, 则对应 i*i 正方形面积也为奇数, 不可能平分, 所以不存在01平衡的
    console.log(0);

    // i 为偶数时
    let count = 0; // 记录01平衡的i*i正方形数量
    for (let r = i; r <= n; r++) {
      for (let c = i; c <= n; c++) {
        // 正方形中1的数量
        const oneCount =
          dp[r][c] - dp[r][c - i] - dp[r - i][c] + dp[r - i][c - i];

        // 如果正方形中1的数量 == 正方形面积的一半，则形成01平衡
        if (oneCount * 2 == i * i) {
          count++;
        }
      }
    }
    console.log(count);
  }

  // 如果 n 是奇数，则上面for循环会遗漏 n*n 正方形的01平衡判断
  if (n % 2 != 0) {
    console.log(0);
  }
})();

Java算法源码

import java.util.Scanner;

public class Main {
    public static void main(String[] args) {
        Scanner sc = new Scanner(System.in);

        int n = Integer.parseInt(sc.nextLine());

        char[][] matrix = new char[n][n];
        for (int i = 0; i < n; i++) {
            matrix[i] = sc.nextLine().toCharArray();
        }

        // 二维数组前缀和
        // dp[i][j] 表示matrix矩阵中以 (i-1, j-1) 位置为右下角点的矩形中1的数量
        int[][] dp = new int[n + 1][n + 1];
        for (int i = 1; i <= n; i++) {
            for (int j = 1; j <= n; j++) {
                // 此处公式请看图示说明
                dp[i][j] = (matrix[i - 1][j - 1] - '0') + dp[i - 1][j] + dp[i][j - 1] - dp[i - 1][j - 1];
            }
        }

        // i 表示正方形边长
        for (int i = 2; i <= n; i += 2) {
            // i 为奇数时, 则对应 i*i 正方形面积也为奇数, 不可能平分, 所以不存在01平衡的
            System.out.println(0);

            // i 为偶数时
            int count = 0; // 记录01平衡的i*i正方形数量
            for (int r = i; r <= n; r++) {
                for (int c = i; c <= n; c++) {
                    // 正方形中1的数量
                    int oneCount = dp[r][c] - dp[r][c - i] - dp[r - i][c] + dp[r - i][c - i];

                    // 如果正方形中1的数量 == 正方形面积的一半，则形成01平衡
                    if (oneCount * 2 == i * i) {
                        count++;
                    }
                }
            }
            System.out.println(count);
        }

        // 如果 n 是奇数，则上面for循环会遗漏 n*n 正方形的01平衡判断
        if (n % 2 != 0) {
            System.out.println(0);
        }
    }
}

Python算法源码

# 输入获取
n = int(input())
matrix = [input() for _ in range(n)]

# 核心代码
if __name__ == '__main__':
    # 二维数组前缀和
    # dp[i][j] 表示matrix矩阵中以 (i-1, j-1) 位置为右下角点的矩形中1的数量
    dp = [[0] * (n + 1) for _ in range(n + 1)]

    for i in range(1, n + 1):
        for j in range(1, n + 1):
            # 此处公式请看图示说明
            dp[i][j] = int(matrix[i - 1][j - 1]) + dp[i - 1][j] + dp[i][j - 1] - dp[i - 1][j - 1]

    # i 表示正方形边长
    for i in range(2, n + 1, 2):
        # i 为奇数时, 则对应 i*i 正方形面积也为奇数, 不可能平分, 所以不存在01平衡的
        print(0)

        # i 为偶数时
        count = 0  # 记录01平衡的i*i正方形数量
        for r in range(i, n + 1):
            for c in range(i, n + 1):
                # 正方形中1的数量
                oneCount = dp[r][c] - dp[r][c - i] - dp[r - i][c] + dp[r - i][c - i]

                # 如果正方形中1的数量 == 正方形面积的一半，则形成01平衡
                if oneCount * 2 == i * i:
                    count += 1

        print(count)

    # 如果 n 是奇数，则上面for循环会遗漏 n*n 正方形的01平衡判断
    if n % 2 != 0:
        print(0)

C算法源码

#include <stdio.h>

#define MAX_SIZE 201

int main() {
    int n;
    scanf("%d", &n);

    char matrix[MAX_SIZE][MAX_SIZE] = {'\0'};
    for (int i = 0; i < n; i++) {
        scanf("%s", matrix[i]);
    }

    // 二维数组前缀和
    // dp[i][j] 表示matrix矩阵中以 (i-1, j-1) 位置为右下角点的矩形中1的数量
    int dp[MAX_SIZE][MAX_SIZE] = {0};
    for (int i = 1; i <= n; i++) {
        for (int j = 1; j <= n; j++) {
            // 此处公式请看图示说明
            dp[i][j] = (matrix[i - 1][j - 1] - '0') + dp[i - 1][j] + dp[i][j - 1] - dp[i - 1][j - 1];
        }
    }

    // i 表示正方形边长
    for (int i = 2; i <= n; i += 2) {
        // i 为奇数时, 则对应 i*i 正方形面积也为奇数, 不可能平分, 所以不存在01平衡的
        puts("0");

        // i 为偶数时
        int count = 0; // 记录01平衡的i*i正方形数量
        for (int r = i; r <= n; r++) {
            for (int c = i; c <= n; c++) {
                // 正方形中1的数量
                int oneCount = dp[r][c] - dp[r][c - i] - dp[r - i][c] + dp[r - i][c - i];

                // 如果正方形中1的数量 == 正方形面积的一半，则形成01平衡
                if (oneCount * 2 == i * i) {
                    count++;
                }
            }
        }
        printf("%d\n", count);
    }

    // 如果 n 是奇数，则上面for循环会遗漏 n*n 正方形的01平衡判断
    if (n % 2 != 0) {
        puts("0");
    }

    return 0;
}

C++算法源码

#include <bits/stdc++.h>
using namespace std;

int main() {
    int n;
    cin >> n;

    vector<string> matrix(n);
    for (int i = 0; i < n; i++) {
        cin >> matrix[i];
    }

    // 二维数组前缀和
    // dp[i][j] 表示matrix矩阵中以 (i-1, j-1) 位置为右下角点的矩形中1的数量
    vector<vector<int>> dp(n + 1, vector<int>(n + 1, 0));
    for (int i = 1; i <= n; i++) {
        for (int j = 1; j <= n; j++) {
            // 此处公式请看图示说明
            dp[i][j] = (matrix[i - 1][j - 1] - '0') + dp[i - 1][j] + dp[i][j - 1] - dp[i - 1][j - 1];
        }
    }

    // i 表示正方形边长
    for (int i = 2; i <= n; i += 2) {
        // i 为奇数时, 则对应 i*i 正方形面积也为奇数, 不可能平分, 所以不存在01平衡的
        cout << 0 << endl;

        // i 为偶数时
        int count = 0; // 记录01平衡的i*i正方形数量
        for (int r = i; r <= n; r++) {
            for (int c = i; c <= n; c++) {
                // 正方形中1的数量
                int oneCount = dp[r][c] - dp[r][c - i] - dp[r - i][c] + dp[r - i][c - i];

                // 如果正方形中1的数量 == 正方形面积的一半，则形成01平衡
                if (oneCount * 2 == i * i) {
                    count++;
                }
            }
        }

        cout << count << endl;
    }

    // 如果 n 是奇数，则上面for循环会遗漏 n*n 正方形的01平衡判断
    if (n % 2 != 0) {
        cout << 0 << endl;
    }

    return 0;
}