目录
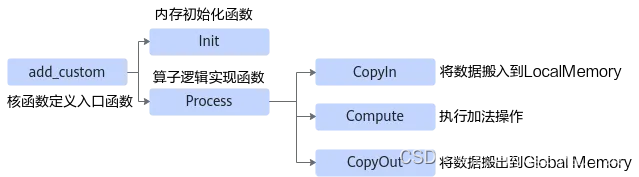
线性代数基础概念:矩阵
1. 矩阵的定义
2. 矩阵的运算
3. 矩阵的特殊类型
4. 矩阵的秩
5. 矩阵的初等变换
6. 矩阵的特征值与特征向量
7. 矩阵的应用
8. 矩阵总结
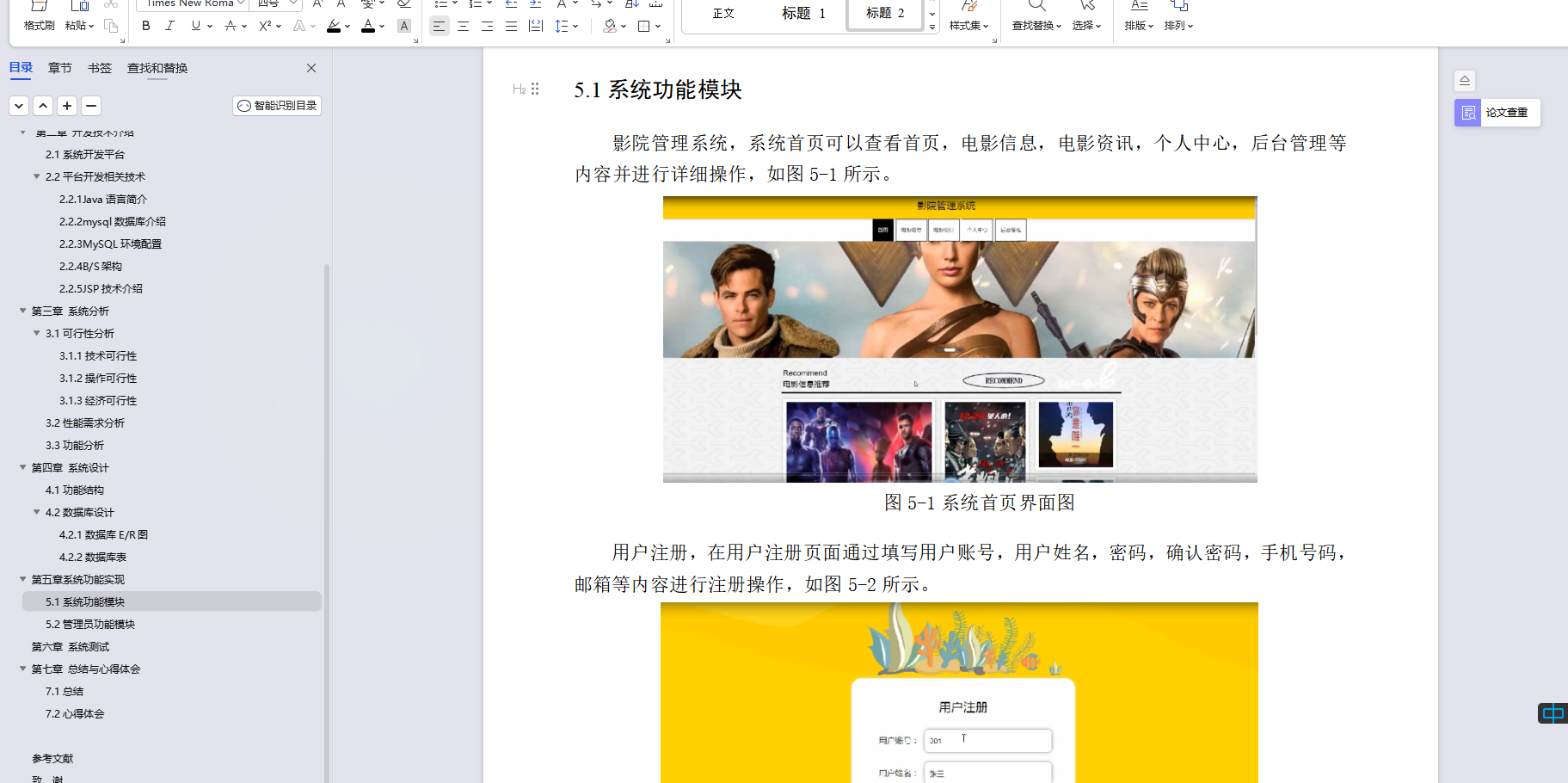
总结
线性代数基础概念:矩阵
矩阵是线性代数中的另一个重要概念,它可以用来表示线性变换、存储数据、解决线性方程组等。
1. 矩阵的定义
矩阵 是一个由数字排列成的矩形数组。
例如:
A = [ 1 2 3 ]
[ 4 5 6 ]
这是一个 2 行 3 列的矩阵,我们称之为 2×3 矩阵。
矩阵的元素 用 aij 表示,其中 i 表示行号,j 表示列号。
例如: 矩阵 A 中的元素 a12 = 2,a21 = 4。
2. 矩阵的运算
矩阵可以进行以下运算:
- 加法: 两个相同大小的矩阵相加,对应元素相加。
- 减法: 两个相同大小的矩阵相减,对应元素相减。
- 数乘: 一个矩阵乘以一个数,矩阵中的每个元素都乘以该数。
- 乘法: 两个矩阵相乘,需要满足一定的条件:第一个矩阵的列数必须等于第二个矩阵的行数。乘积矩阵的元素为第一个矩阵的行向量与第二个矩阵的列向量的点积。
例如:
A = [ 1 2 ]
[ 3 4 ]
B = [ 5 6 ]
[ 7 8 ]
A + B = [ 6 8 ]
[ 10 12 ]
A - B = [ -4 -4 ]
[ -4 -4 ]
2A = [ 2 4 ]
[ 6 8 ]
AB = [ 19 22 ]
[ 43 50 ]
3. 矩阵的特殊类型
- 零矩阵: 所有元素都为 0 的矩阵。
- 单位矩阵: 对角线元素为 1,其他元素为 0 的方阵。
- 对角矩阵: 只有对角线元素不为 0 的方阵。
- 上三角矩阵: 对角线以下的元素都为 0 的方阵。
- 下三角矩阵: 对角线以上的元素都为 0 的方阵。
- 对称矩阵: 满足 A = AT 的方阵。
- 反对称矩阵: 满足 A = -AT 的方阵。
4. 矩阵的秩
矩阵的秩 是矩阵中线性无关的行向量或列向量的最大个数。
例如:
A = [ 1 2 3 ]
[ 4 5 6 ]
[ 7 8 9 ]
矩阵 A 的秩为 2,因为矩阵 A 中只有两行线性无关。
5. 矩阵的初等变换
矩阵的初等变换 是指对矩阵进行以下三种操作:
- 交换两行或两列。
- 将一行或一列乘以一个非零数。
- 将一行或一列加上另一行或列的倍数。
初等变换不会改变矩阵的秩。
6. 矩阵的特征值与特征向量
特征值 是一个数,它满足以下方程:
Ax = λx
其中 A 是一个矩阵,x 是一个非零向量,λ 是一个数。
特征向量 是一个非零向量 x,它满足上述方程。
特征值和特征向量是矩阵的重要性质,它们可以用来分析矩阵的性质,例如矩阵的稳定性、可对角化性等。
7. 矩阵的应用
矩阵在很多领域都有广泛的应用,例如:
- 线性方程组的求解: 矩阵可以用来表示线性方程组,并用高斯消元法求解。
- 线性变换的表示: 矩阵可以用来表示线性变换,例如旋转、平移、缩放等。
- 数据存储: 矩阵可以用来存储数据,例如图像、音频、视频等。
- 机器学习: 矩阵在机器学习中扮演着重要的角色,例如神经网络、支持向量机等。
8. 矩阵总结
| 概念 | 描述 |
|---|---|
| 矩阵 | 由数字排列成的矩形数组 |
| 矩阵的元素 | 用 aij 表示,其中 i 表示行号,j 表示列号 |
| 矩阵的运算 | 加法、减法、数乘、乘法 |
| 矩阵的特殊类型 | 零矩阵、单位矩阵、对角矩阵、上三角矩阵、下三角矩阵、对称矩阵、反对称矩阵 |
| 矩阵的秩 | 矩阵中线性无关的行向量或列向量的最大个数 |
| 矩阵的初等变换 | 交换两行或两列、将一行或一列乘以一个非零数、将一行或一列加上另一行或列的倍数 |
| 矩阵的特征值与特征向量 | 满足 Ax = λx 的数 λ 和非零向量 x |
| 矩阵的应用 | 线性方程组的求解、线性变换的表示、数据存储、机器学习 |
总结
矩阵是线性代数中的重要概念,它可以用来表示线性变换、存储数据、解决线性方程组等。理解矩阵的定义、运算、特殊类型、秩、初等变换、特征值与特征向量等概念,是学习线性代数的关键。