前言1:这篇博客仅限于介绍拉格朗日乘子法,KKT条件,ALM算法,ADMM算法等最优化方法的使用以及简版代码实现,但不会涉及具体的数学推导;不过在下面我会给出具体数学推导的相关文章和截图,供学有余力的同志参考;
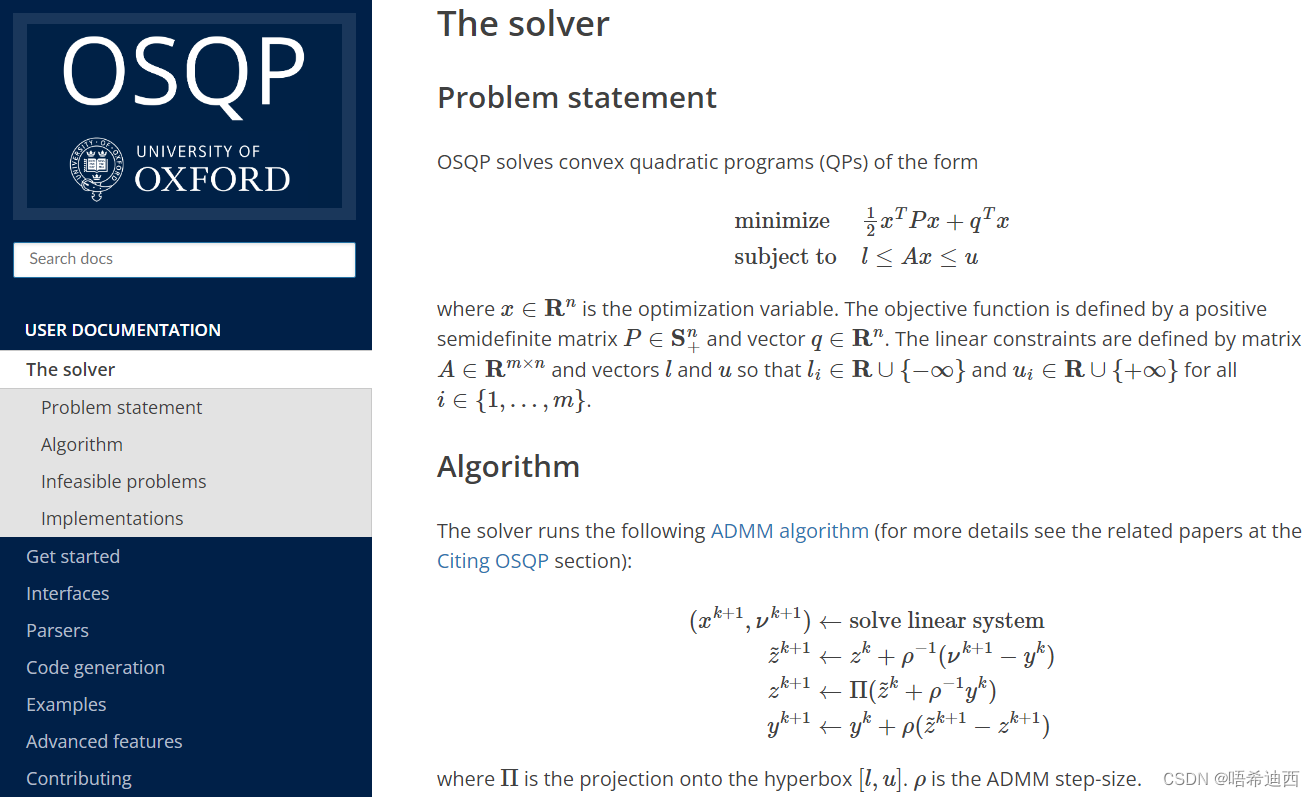
前言2:从OSQP求解器的官方网站可以得知,OSQP求解器使用的最优化方法即ADMM算法;
a
a
a
a
a
a
1. 拉格朗日乘子法与KKT条件
注:这一章节不从数学推导上,而是从实际数学意义上,直观的讲解拉格朗日乘子法和KKT条件是如何推导得来的;
1.1 无约束的优化问题 -- 梯度下降法
首先从无约束的优化问题讲起,一般就是要使表达式 取到最小值;对于这类问题在高中就学过怎么做,只要对它的每一个变量求导,然后让偏导为零,解方程组就行了;
在极值点处一定满足 (只是必要条件),然后对它进行求解,再代入验证是否真的是极值点就行了;
但是有很多问题通过直接求导是解不出来的,或者很难解,所以就需要梯度下降法、牛顿法、坐标下降法之类的数值迭代算法;对于这些迭代算法就像下面这张图一样,我们希望找到其中的最小值,一个比较直观的想法是先找一个起点,然后不断向最低点靠近。就先把一个小球放到一个碗里一样;
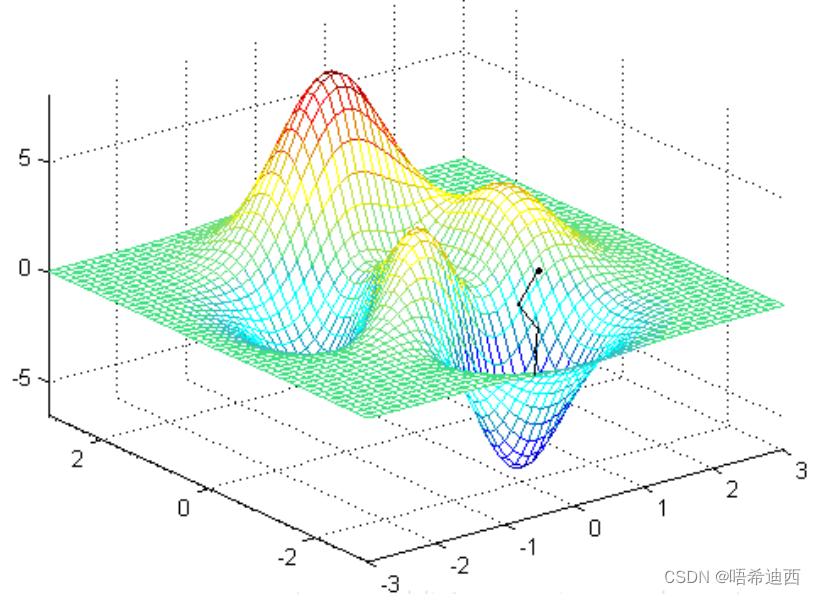
一开始要找一个起始点,然后确定走的方向和距离,最后还要知道什么时候停止;这三步中最难的是确定走的方向,走的慢点还可以接受,要是方向错了就找不到最小值了;
- 走的距离可以简单的设为一个比较小的值;
- 起始点可以随机选一个
;
- 关键是方向,可以选择
处的梯度的反方向,这是函数在这个点下降最快的方向;
- 最终的停止条件是梯度的大小很接近于 0(在极值点处的梯度大小就是 0);
这种方法依靠梯度确定下降方向的方法叫做梯度下降法;
对 求极小值的流程:
- 随机选定起点
- 得到函数在
的梯度,然后从
向前走一步(
)
- 重复第2步,直到梯度接近于0(小于一个事先设定的小值),或到达指定的迭代次数上限
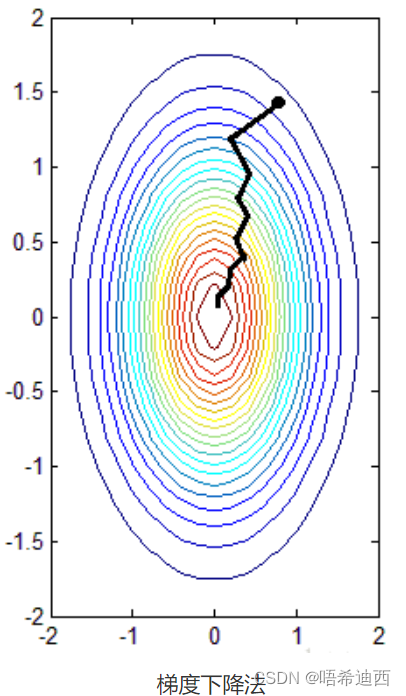
1.2 有约束优化问题 -- 拉格朗日乘子法和KKT条件
摘自文章:
- https://www.cnblogs.com/xinchen1111/p/8804858.html
- 什么是仿射函数?-CSDN博客
- https://www.cnblogs.com/fuleying/p/4481334.html
a
a
1.2.1 单个等式约束
我们可能要在满足一定约束条件的情况下最小化目标函数,比如有一个等式约束:
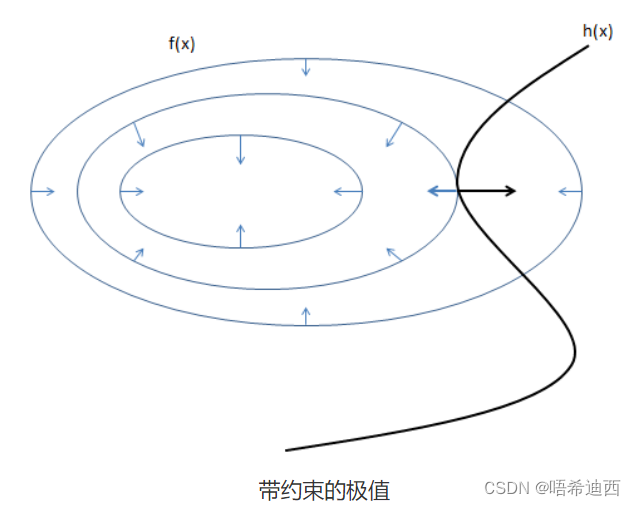
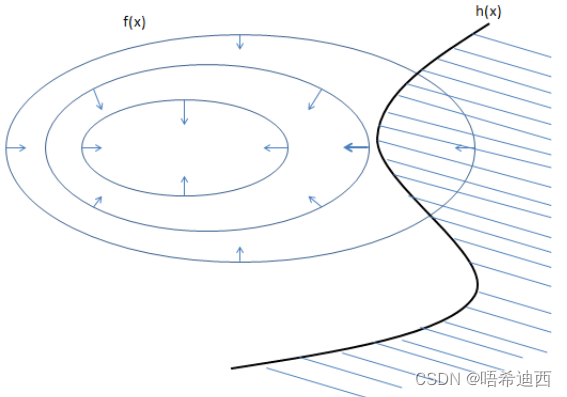
如图,其中的圆圈是目标函数 𝑓(𝑥,𝑦) 投影在平面上的等值线,黑线是约束条件 ℎ(𝑥)=0 的函数图像;等值线与函数图像相交的点其实就是所有满足约束的点;
那么极值点只有可能在等值线与函数图像相切的地方取到,因为如果在相交的地方取到,那么沿着 ℎ(𝑥) 的图像往前走或者往后走,一定还有其它的等值线与它相交,也就是 𝑓(𝑥,𝑦) 的值还能变大和变小,所以交点不是极值点,只有相切的时候才有可能是极值点(不可能同时变大和变小,往前后两个方向走只能同时变大/变小,这才是极值点);
在相切的地方 ℎ(𝑥) 的梯度和 𝑓(𝑥,𝑦) 的梯度应该是在同一条直线上的(在切点处两个函数的梯度都与切平面垂直,所以在一条直线上);
所以满足条件的极值点一定满足:∇𝑓(𝑥,𝑦)=𝜆∇ℎ(𝑥,𝑦) 和 ℎ(𝑥,𝑦)=0
那么只要解出这个方程组,就可以得到问题的解析解了;当然也存在解不出来的情况,就需要用罚函数法之类的方法求数值解了;
为了方便和好记,就把原来的优化问题写成 𝑓(𝑥,𝑦)+𝜆ℎ(𝑥,𝑦) 的形式,然后分别对 𝜆,𝑥,𝑦 求偏导,并且令偏导为 0 就行了(对 x,y 的偏导为0可以得到式子 ∇𝑓(𝑥,𝑦)-𝜆∇ℎ(𝑥,𝑦)=0 )( 对 𝜆 的偏导为0可以得到式子 ℎ(𝑥,𝑦)=0 ),和之前得到的方程组是一样的;这种方法叫拉格朗日乘数法;
a
a
1.2.2 多个等式约束
将拉格朗日乘子法扩展到含有多个等式约束的情况:
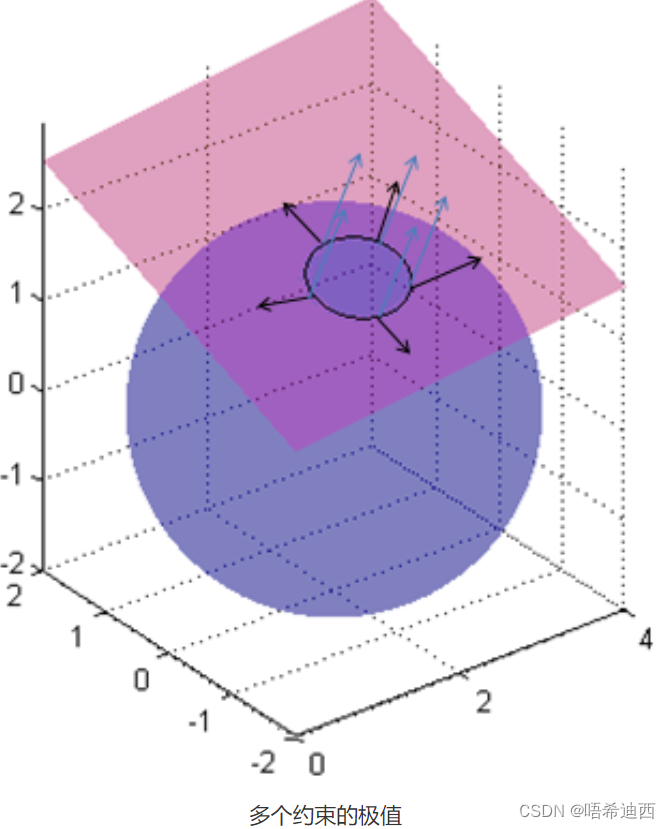
这里的平面和球面分别代表了两个约束 ℎ1(𝑥) 和 ℎ2(𝑥),那么这个问题的可行域就是它们相交的那个圆;这里蓝色箭头表示平面的梯度,黑色箭头表示球面的梯度,那么相交的圆的梯度就是它们的线性组合,所以在极值点处目标函数的梯度和约束的梯度的线性组合在一条直线上,所以满足:
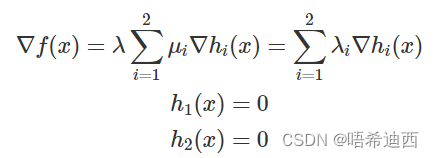
为了好记,将原来的约束的问题写成 的形式,然后对 𝑥、𝜆 求偏导,让它们为 0;结果像上面一样直接列方程组是一样的,这可以看做是一种简记,或者是对偶问题,这个函数叫做拉格朗日函数;
a
a
1.2.3 同时含有等式约束和不等式约束
如果问题中既有等式约束,又有不等式约束怎么办呢?对于:
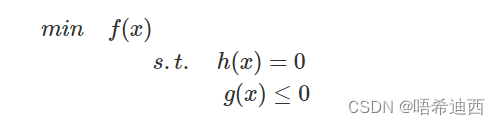
当然也同样约定不等式是 ≤,如果是 ≥ 只要取反就行了;
对于这个问题先不看等式约束,对于不等式约束和目标函数的图:
阴影部分就是可行域,也就是说可行域从原来的一条线变成了一块区域;那么能取到极值点的地方可能有两种情况:
- 还是在 ℎ(𝑥) 和 等值线相切的地方
- 𝑓(𝑥) 的极值点本身就在可行域里面
因为如果不是相切,那么同样的,对任意一个在可行域中的点,如果在它附近往里走或者往外走,𝑓(𝑥) 一般都会变大或者变小,所以绝大部分点都不会是极值点;除非这个点刚好在交界处,且和等值线相切;或者这个点在可行域内部,但是本身就是 f(x)𝑓(𝑥) 的极值点;
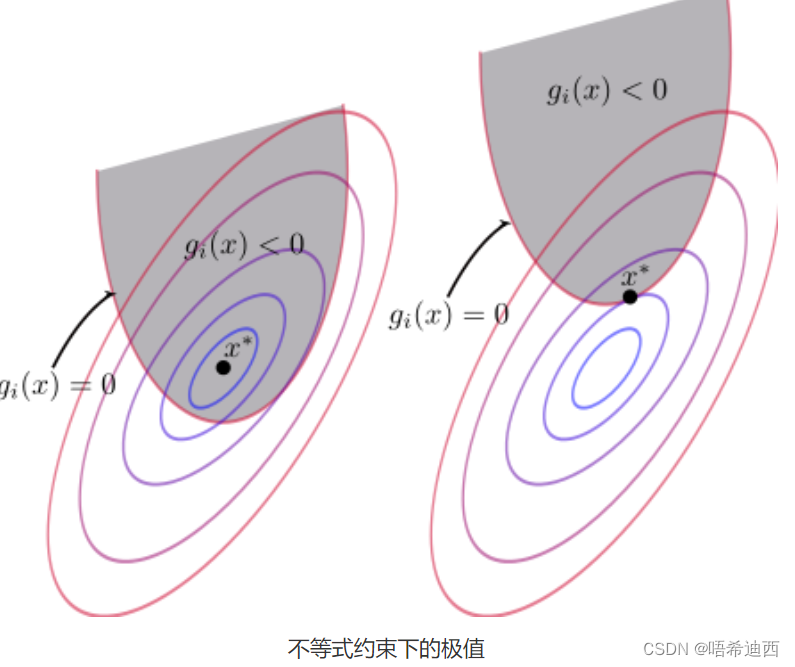
对于第一种情况,不等式约束就变成等式约束了,对 𝑓(𝑥)+𝜆ℎ(𝑥)+𝜇𝑔(𝑥) 用拉格朗日乘子法:
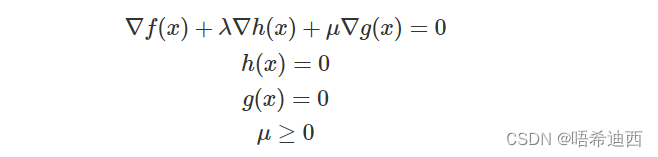
对于第二种情况,不等式约束就相当于没有,对 𝑓(𝑥)+𝜆ℎ(𝑥) 用拉格朗日乘子法:
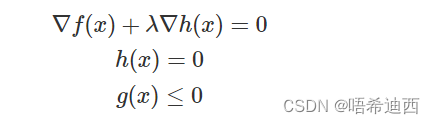
把两种情况用同一组方程表示出来,对比一下两个问题:
- 第一种情况中有 𝜇≥0 且 𝑔(𝑥)=0
- 第二种情况 𝜇=0 且 𝑔(𝑥)≤0
综合两种情况,可以写成 𝜇𝑔(𝑥)=0 且 𝜇≥0 且 𝑔(𝑥)≤0:
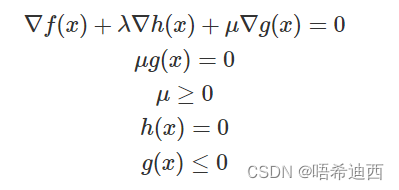
这个就是 KKT 条件;它的含义是这个优化问题的极值点一定满足这组方程组(不是极值点也可能会满足,但是不会存在某个极值点不满足的情况);它也是原来的优化问题取得极值的必要条件,解出来了极值点之后还是要代入验证的,但是因为约束比较多,情况比较复杂,KKT 条件并不是对于任何情况都是满足的;
要满足 KKT 条件需要有一些规范性条件(Regularity conditions),就是要求约束条件的质量不能太差,常见的比如:
- LCQ:如果 ℎ(𝑥) 和 𝑔(𝑥) 都是形如 𝐴𝑥+𝑏 的仿射函数,那么极值一定满足 KKT 条件;
- LICQ:起作用的 𝑔(𝑥) 函数(即 𝑔(𝑥) 相当于等式约束的情况)和 ℎ(𝑥) 函数在极值点处的梯度要线性无关,那么极值一定满足 KKT 条件;
- Slater 条件:如果优化问题是个凸优化问题,且至少存在一个点满足 ℎ(𝑥)=0 和 𝑔(𝑥)=0,极值一定满足 KKT 条件,并且满足强对偶性质;
a
a
a
a
a
a
2. ALM 算法
注1:ALM(Augmented Lagrange Multiplier)算法,即增广型拉格朗日乘子法
注2:ALM 算法常用于线性规划问题( 不能有高阶项/根号项,也不能有两个变量之间的交乘积项);
注3:ALM 算法的推导过程 -- http://faculty.bicmr.pku.edu.cn/~wenzw/optbook/lect/16-lect-alm.pdf
2.1 ALM 算法介绍
只考虑含有等式约束的问题:
a
a
注:含有不等式约束问题的 ALM 算法,见文章 -- http://faculty.bicmr.pku.edu.cn/~wenzw/optbook/lect/16-lect-alm.pdf
构造增广拉格朗日函数:
:拉格朗日乘子(矩阵)
:惩罚项权重(标量)
a
a
注意:增广拉格朗日乘子法就是在拉格朗日乘子法获得的函数后面,加上针对所有等式约束的惩罚项;
a
a
优点:
- 原拉格朗日函数的收敛性不太好,抖动很大不稳定;
- 加上了惩罚项可以增加原拉格朗日函数的凸性,使得我们可以通过更简单的方法,如梯度下降法去求解这个函数的最优解;
- 加强了等式约束的限制作用(针对等式约束增加了惩罚项),使得在迭代的过程中迭代点一直是在约束附近的区域进行梯度下降,不会跑太远,从而加快了求解速度;
ALM 算法的求解过程:梯度下降
- 先对变量
进行梯度下降:
- 再对拉格朗日乘子
进行梯度下降:
- 上述两步为一次迭代,不断这样迭代下去,直至收敛或者到达指定迭代次数;
2.2 ALM 算法代码示例
举例:只含等式约束
a
使用 Scipy 中的函数 linprog 求解线性规划问题,将求解得到的结果作为参考答案:
函数 linprog:scipy.optimize.linprog函数参数最全详解_optimize的linprog-CSDN博客
"""
solve the following problem with scipy
min f(x) = -3x[0] - 5x[1]
s.t. x[0] + x[2] = 4
2x[1] + x[3] = 12
3x[0] + 2x[1] + x[4] = 18
x[0], x[1], x[2], x[3], x[4] >= 0
optimal solution:
fun: -36.0
x: [ 2.000e+00 6.000e+00 2.000e+00 0.000e+00 0.000e+00]
"""
from scipy.optimize import linprog
import torch
c = torch.tensor([-3, -5, 0, 0, 0], dtype=torch.float32)
A = torch.tensor([[1, 0, 1, 0, 0], [0, 2, 0, 1, 0], [3, 2, 0, 0, 1]], dtype=torch.float32)
b = torch.tensor([4, 12, 18], dtype=torch.float32)
res = linprog(c, A_eq=A, b_eq=b, bounds=(0, None))
print(res)a
ALM 算法示例:
"""
solve the following problem with Augmented Lagrange Multiplier method
min f(x) = -3x[0] - 5x[1]
s.t. x[0] + x[2] = 4
2x[1] + x[3] = 12
3x[0] + 2x[1] + x[4] = 18
x[0], x[1], x[2], x[3], x[4] >= 0
问题形式:
min f(x) = c^T x
s.t. Ax = b
x >= 0
"""
import torch
def lagrangian_function(x, lambda_):
return f(x) + lambda_ @ (A @ x - b) + alpha / 2 * ((A @ x - b)**2).sum()
def f(x):
return c @ x
def update_x(x, lambda_):
""" update x with gradient descent """
lagrangian_function(x, lambda_).backward()
new_x = x - eta * x.grad
x.data = new_x.clamp(min=0)
x.grad.zero_()
def update_lambda(lambda_):
new_lambda = lambda_ + alpha * (A @ x - b)
lambda_.data = new_lambda
def pprint(i, x, lambda_):
print(f'\n{i+1}th iter, L:{lagrangian_function(x, lambda_):.2f}, f: {f(x):.2f}')
print(f'x: {x}')
print(f'lambda: {lambda_}')
print("constraints violation: ")
print(A @ x - b)
def solve(x, lambda_):
for i in range(500):
pprint(i, x, lambda_) # 更新 x
update_x(x, lambda_) # 更新拉格朗日乘子
update_lambda(lambda_) # 打印信息
if __name__ == '__main__':
eta = 0.03 # 学习率
alpha = 1 # 惩罚权重
c = torch.tensor([-3, -5, 0, 0, 0], dtype=torch.float32)
A = torch.tensor([[1, 0, 1, 0, 0], [0, 2, 0, 1, 0], [3, 2, 0, 0, 1]], dtype=torch.float32)
b = torch.tensor([4, 12, 18], dtype=torch.float32)
lambda_ = torch.tensor([0, 0, 0], dtype=torch.float32)
x = torch.tensor([2, 0, 2, 0, 0], dtype=torch.float32, requires_grad=True)
solve(x, lambda_)a
a
a
a
a
a
3. ADMM 算法
注1:ADMM(Alternating Direction Method of Multipliers)算法,即交替方向乘子法
注2:关于详细的数学推导 -- 一文详解从拉格朗日乘子法、KKT条件、对偶上升法到罚函数与增广Lagrangian乘子法再到ADMM算法(交替方向乘子法)_拉格朗日乘子 二次惩罚系数-CSDN博客
3.1 ADMM 算法介绍
只考虑含有等式约束的问题:
a
a
和ALM算法的不同点在于:将所有的变量分成几部分(假设为两部分,一部分是向量
,一部分是向量
),然后分别进行梯度下降,而不是一次性将所有的变量全部都进行梯度下降;
构造增广拉格朗日函数:
:拉格朗日乘子(矩阵)
:惩罚项权重(标量)
ADMM 算法的求解过程:
- 先对变量
进行梯度下降:
- 再对变量
进行梯度下降:
- 再对变量
进行梯度下降:
- 上述三步为一次迭代,不断这样迭代下去,直至收敛或者到达指定迭代次数;
3.2 ADMM 算法代码示例
"""
solve the following problem with Alternating Direction Multiplier Method
min f(x) = -3x[0] - 5x[1]
s.t. x[0] + x[2] = 4
2x[1] + x[3] = 12
3x[0] + 2x[1] + x[4] = 18
x[0], x[1], x[2], x[3], x[4] >= 0
问题形式:
min f(x) = c^T x
s.t. Ax = b
x >= 0
"""
import torch
def lagrangian_function(x, lambda_):
return f(x) + lambda_ @ (A @ x - b) + alpha / 2 * ((A @ x - b)**2).sum()
def f(x):
return c @ x
def update_x(x, lambda_):
""" update x with gradient descent """
for i in range(len(x)):
# not the best way to calculate gradient
# 这里直接将所有的变量拆成了5份,这并不是最好的求解方式
lagrangian_function(x, lambda_).backward()
x_i = x[i] - eta * x.grad[i]
x.data[i] = max(0, x_i)
x.grad.zero_()
def update_lambda(lambda_):
new_lambda = lambda_ + alpha * (A @ x - b)
lambda_.data = new_lambda
def pprint(i, x, lambda_):
print(f'\n{i+1}th iter, L:{lagrangian_function(x, lambda_):.2f}, f: {f(x):.2f}')
print(f'x: {x}')
print(f'lambda: {lambda_}')
print("constraints violation: ")
print(A @ x - b)
def solve(x, lambda_):
for i in range(500):
pprint(i, x, lambda_)
update_x(x, lambda_)
update_lambda(lambda_)
if __name__ == '__main__':
eta = 0.03 # 学习率
alpha = 1 # 惩罚权重
c = torch.tensor([-3, -5, 0, 0, 0], dtype=torch.float32)
A = torch.tensor([[1, 0, 1, 0, 0], [0, 2, 0, 1, 0], [3, 2, 0, 0, 1]], dtype=torch.float32)
b = torch.tensor([4, 12, 18], dtype=torch.float32)
lambda_ = torch.tensor([0, 0, 0], dtype=torch.float32)
x = torch.tensor([2, 0, 2, 0, 0], dtype=torch.float32, requires_grad=True)
solve(x, lambda_)