文章目录
- 引言
- 复习
- 单调队列优化——最大子序列和
- 思路分析
- 实现代码
- 参考实现
- 背包问题——宠物小精灵的收服问题
- 个人实现
- 参考实现
- 新作
- 两两交换链表中的节点
- 个人实现
- 参考实现
- 删除有序数组中的重复项
- 个人实现
- 知识补全
- 迭代器的访问和控制
- vector删除特定的元素erase
- vector底层删除元素的原理是什么?
- 实现思路
- 总结
引言
- 今天早上起的刚好,挺早的,书也背了,继续开始复习。动态规划的章节继续完成。
复习
单调队列优化——最大子序列和
- 第一次的理论推理
- 第二次代码推理
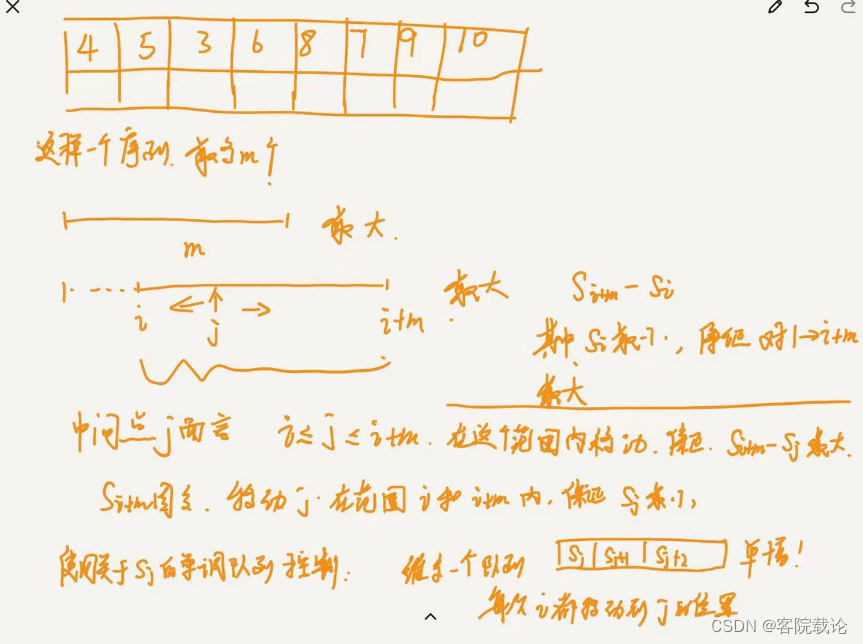
思路分析
- 这个题目是在长度为n的整数序列,找出长度不超过m的连续子序列,最直白的做法就是的枚举起点,然后在遍历终点。现在转换为找在范围m内移动坐标点,使得该坐标点的累加和最小,为了一个单调递增队列实现。
下面分析,知道问题转换部分都是确定的,但是后续部分就有点不确定了,参考一下就行,感觉有点硬往单调队列上车扯
实现代码
#include <iostream>
using namespace std;
const int N = 300010,M = 300010;
int s[N],q[N];
int n,m; // n是队列元素个数,m是维系的m个队列
int main(){
cin>>n>>m;
// 维系累加和队列
for (int i = 1; i <= n; ++i) {
cin>>s[i];
s[i] += s[i - 1];
}
// 计算单调最优队列
int res = INT_MIN;
int l = 0,r = 0;
for (int i = 1; i <= n; ++i) {
// 判定队列是否超过了当前的边界只
if (l <= i && i - q[l] > m) l ++;
res = max(res,s[i] - s[q[l]]);
// 更新最右端队列的边界值
// 右指针移动的时候,是如何进行比较的
int t = q[r] + 1;
// 保证队列的右指针始终在左指针旁边
while (r >= l && s[q[r]] > s[t]) r--;
q[++r] = t;
}
cout<<res;
}
问题
- 在实现中,不知道单调递增队列应该如何和右指针进行比较,所以迭代的细节不是很清楚。我以为的迭代过程是在i-m到i之内,结果不对,或者说过程不对,如果抛开的m这个边界不说,那就是直接找s[i]的最小值的,也就是的往后遍历即可。
- 我这里是遍历到的q[r]右边的一个元素,和那个差不多。因为在i不断增加的过程中,实际上,就已经控制了边界,每一次都是遍历到i,那么在i为i-1的时候,其实就已经遍历过对应的值了。
参考实现
#include <iostream>
#include <limits.h>
using namespace std;
typedef long long LL;
const int N = 300010;
int q[N],s[N];
int n,m;
int main(){
cin>>n>>m;
for (int i = 1; i <= n ; ++i) {
cin>>s[i];
s[i] += s[i - 1];
}
// 创建对应的队列
int hh = 0,tt = 0,res = INT_MIN;
q[hh] = 0;
for (int i = 1; i <= n; ++i) {
// 保证队列的长度不变
if (i - q[hh] > m) hh++;
// 计算最值
res = max(res , s[i] - s[q[hh]]);
// 更新的队列尾部
// 队列可为空,也就是tt >= hh
// 然后就是保证队列是单调递增的,如果出现新的值小于后续的值,
// 就要将所有比之大的数据排除,因为是一个序列,一定会选中这个数据
while(tt >= hh && s[q[tt]] > s[i]) tt --;
// 移动到一个小于或者等于的数字之后,tt再往后移动一个,即将新的排序值,加入其中。
q[++tt] = i;
}
cout<<res;
}
背包问题——宠物小精灵的收服问题
- 第一次做的链接
- 上一次大概看了一遍,是一个二维背包问题,但是二维背包问题怎么做还有点不清楚的。应该是两个维度,基本上所有的状态分析都是对的。
个人实现
#include <iostream>
using namespace std;
const int N = 10010,M = 510,K = 110; // N精灵球的数量,M皮卡丘的初始体力值,K是野生小精灵的数量
int n,m,k;
int f[K][N][M];
int mt[K],nt[K];
int main(){
cin>>n>>m>>k;
for (int i = 0; i < k; ++i) {
cin>>nt[i]>>mt[i];// 分别记录收服每一个小精灵的数量、损耗的体力值
}
// 动态规划方程
// 初始值的问题
for (int i = 0; i < k; ++i) {
for (int j = 0; j < m; ++j) {
// 遍历对应皮神的体力值
for (int l = 0; l < n; ++l) {
// 遍历手上剩余的精灵球的数量
// 主要是两种情况,分别是抓或者不抓
if (i - 1 >= 0 && j - mt[i] >= 0 && l - nt[i]>= 0)
f[i][j][l] = max(f[i - 1][j][l],f[i - 1][j - mt[i]][l - nt[i]] + 1);
}
}
}
// 现在是遍历右下角,然后遍历精灵球用光的场景
int res = f[k - 1][m - 1][n - 1];
for (int i = 0; i < n; ++i) {
res = max(res,f[k - 1][m - 1][i]);
}
cout<<res;
}
问题
如何初始化?
- 这里默认初始化为零,就行了。
定边技巧如何实现?
- 这里是使用滚动数组实现的,然后倒序遍历控制了临界条件,总的来说,我的方法也是保证了临界条件,但是滚动数组优化效果会更好。
选择哪个维度最大进行遍历?
- 这里仅仅选择要求的维度进行遍历,比如这里的就是选择体力值这个维度进行遍历,然后精灵球一定是用完的,如果精灵球没有用完,那么所收服的数量一定是小于等于精灵球用完的情况。这里是同样的。
参考实现
- 下面是自己根据理解和记忆修改的
- 以下几个地方需要注意
- 关于体力值的遍历,应该从n-1开始,体力值不能用完,皮神不能死。
#include <iostream>
using namespace std;
const int N = 1010,M = 510,K = 110; // N精灵球的数量,M皮卡丘的初始体力值,K是野生小精灵的数量
int n,m,k;
int f[M][N];
int mt[K],nt[K];
int main(){
cin>>n>>m>>k;
for (int i = 1; i <= k; ++i) {
cin>>nt[i]>>mt[i];// 分别记录收服每一个小精灵的数量、损耗的体力值
}
// 动态规划方程
// 初始值的问题
for (int i = 1; i <= k; ++i) {
for (int j = m - 1; j >= mt[i]; j--) {
// 遍历对应皮神的体力值
for (int l = n ; l >= nt[i]; l--) {
// 遍历手上剩余的精灵球的数量
f[j][l] = max(f[j][l],f[j - mt[i]][l - nt[i]] + 1);
}
}
}
// 现在是遍历右下角,然后遍历精灵球用光的场景
int res = f[m - 1][n];
cout<<res<<" ";
int cost_m = m;
for (int i = 0; i <= m - 1; ++i) {
if (res == f[i][n])
cost_m = min(cost_m,i);
}
cout<<m - cost_m;
}
新作
两两交换链表中的节点
- 题目链接
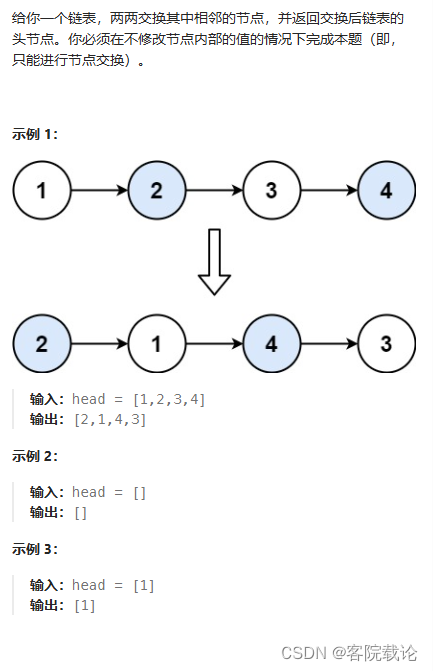
个人实现
- 这道题单纯是模拟整个过程进行实现,然后是两个指针进行遍历,实际上可能只需要一个指针的。
#include <iostream>
using namespace std;
struct ListNode{
int val;
ListNode* next;
ListNode(int x,ListNode* y):val(x),next(y){};
ListNode(int x):val(x),next(nullptr){};
ListNode():val(-1),next(nullptr){};
};
ListNode* swapPairs(ListNode* head){
auto dummy = new ListNode();
dummy->next = head;
// 交换链表
auto l = dummy,r = head;
while( r && r->next){
// 交换链表,然后更换数据
l->next= r->next;
r->next = l->next->next;
l->next->next = r;
// 更新对应的左右指针
if (r->next) r = r->next;
l = l->next->next;
}
// 返回最终节点
return dummy->next;
}
int main(){
}
- 少有的再25分钟之内通过了测试。
参考实现
- 总的来说,思路是一样的,但是他的表示还有代码太简洁了,真的,佩服的五体投地,总结一下,主要有以下几个点值得我学习。
- 对于经常使用的变量,没有必要一直写next->next,使用一个变量存一下,不会好很多码?
- 为什么非得就画两个指针,画三个指针不是更好懂吗?
- 看了一遍思路,这里实现一下哎!
整体思路和我的一样的,都是模拟
#include <iostream>
using namespace std;
struct ListNode{
int val;
ListNode* next;
ListNode(int x,ListNode* y):val(x),next(y){};
ListNode(int x):val(x),next(nullptr){};
ListNode():val(-1),next(nullptr){};
};
ListNode* swapPairs(ListNode* head){
auto dummy = new ListNode();
dummy->next = head;
// 交换链表
for (auto p = dummy;p->next && p->next->next;) {
auto a = p->next,b = p->next->next;
p->next = b;
a->next = b->next;
b->next = a;
p = a;
}
// 返回最终节点
return dummy->next;
}
int main(){
}
删除有序数组中的重复项
- 题目链接


个人实现
- 整个题很简单,就是遍历一遍,但是有一个问题,就是vector怎么实现删除特定索引的元素?
编程遇到的问题 - vector如何删除特定索引的元素?
- 使用迭代器遍历元素,如何获取元素具体的值?
- 迭代器怎么访问?
#include <iostream>
#include <vector>
using namespace std;
int removeDuplicates(vector<int> & nums){
int l = nums.size();
for (auto x = nums.begin();x < nums.begin() + l;x ++) {
while (x + 1 <= nums.end() && *x == * (x + 1))
nums.erase(x);
}
return nums.size();
}
int main(){
vector<int> res = {1,1,2};
cout<<removeDuplicates(res);
}
- 这个代码有很大的问题的,明明实现起来很简单,但是语法不熟悉,无论通过迭代器还是通过索引删除,都会改变原来的结构,索引就不成立了。不能删除,除了开新数组,然后逐个赋值,其他就不知道了。但是这种没意义。这题重要的不是思路,重要的是让我知道有很多知识点不会。
知识补全
迭代器的访问和控制
vector<int> test;
for(auto it = test.begin();it != test.end();it ++){ // 通过+1实现向后迭代
cout<<*it<<endl; // 通过*iterator进行访问
}
vector删除特定的元素erase
使用迭代器进行删除
- 删除特定的元素
nums.erase(nums.begin() + 1);
删除特定范围的元素
nums.erase(nums.begin() + 1,nums.begin() + 3);
vector底层删除元素的原理是什么?
- 找到要删除的元素:使用迭代器或索引找到要删除的元素位置。
- 移动元素:将后续的元素向前移动,以填补被删除元素的位置。
- 调整大小:更新容器的大小,缩减到实际存储的元素数量。
- 所以,使用erase的话,就会出现上述问题,时间复杂度还是很高的,如果能够直接修改对应的size元素,时间效率会更好。
实现思路
- 这道题他妈的没看清楚,实际上有明确指出,只要求前k个元素是不同的单调递增就行了,不要求整个数组都是单调递增的,这里出大问题的。 就是很简单的双指针遍历。
class Solution {
public:
int removeDuplicates(vector<int>& nums) {
int n = nums.size();
if (n == 0) {
return 0;
}
int fast = 1, slow = 1;
while (fast < n) {
if (nums[fast] != nums[fast - 1]) {
nums[slow] = nums[fast];
++slow;
}
++fast;
}
return slow;
}
};
总结
- 尴尬,今天是投论文的第一天,又超时了,上午刷算法用了太多时间,不应该呀。
- 不过对于单调队列还有二维背包有了更深层次的理解。
- 早上两道题,做的还行,复习了一下,都是自己写出来了,虽然超时了。晚上有一道简单题没写出来,很难受,是因为看错了,没理解题目的意思。