每个样本都有标签的机器学习称为监督学习。根据标签数值类型的不同，监督学习又可以分为回归问题和分类问题。分类和回归是监督学习的核心问题。

• 回归(regression)问题中的标签是连续值。
• 分类(classification)问题中的标签是离散值。分类问题根据其类别数量又可分为二分类（binary classification）和多分类（multi-class classification）问题。

线性分类

Logistic 回归

基本形式

给定的数据集
$$D=\{({\mathbf{x}}_1,y_1),({\mathbf{x}}_2,y_2),\cdots ,({\mathbf{x}}_N,y_N\}$$
包含 $N$ 个样本，$p$ 个特征。其中，第 $i$ 个样本的特征向量为 ${\mathbf{x}}_i=(x_{i1},x_{i2},\cdots ,x_{ip}{)}^T$ 。目标变量 y i ∈ { 0 , 1 } y_i\in \{0,1\} yi​∈{0,1} 。逻辑回归试图预测正样本的概率，那我们需要一个输出 $[0,1]$ 区间的激活函数。假设二分类数据集服从均值不同、方差相同的正态分布
$$\{\begin{array}{l}\mathbb{P}(\mathbf{x}|y=1)=\mathcal{N}(\mathbf{x};{\mu }_1,\mathbf{\Sigma })\\ \mathbb{P}(\mathbf{x}|y=0)=\mathcal{N}(\mathbf{x};{\mu }_0,\mathbf{\Sigma })\end{array}$$
其中，协方差矩阵$\mathbf{\Sigma }$ 为对称阵。正态分布概率密度函数为
$$\mathcal{N}(\mathbf{x};\mu ,\mathbf{\Sigma })=\frac{1}{\sqrt{(2\pi {)}^p\det \mathbf{\Sigma }}}\exp \left(-\frac{1}{2}(\mathbf{x}-\mu {)}^T{\mathbf{\Sigma }}^{-1}(\mathbf{x}-\mu )\right)$$
利用贝叶斯定理，正样本条件概率
$$\mathbb{P}(y=1|\mathbf{x})=\frac{\mathbb{P}(\mathbf{x}|y=1)\mathbb{P}(y=1)}{\mathbb{P}(\mathbf{x}|y=0)\mathbb{P}(y=0)+\mathbb{P}(\mathbf{x}|y=1)\mathbb{P}(y=1)}$$
令 [^cdot]
$$\begin{array}{rl}z& =\ln \frac{\mathbb{P}(\mathbf{x}|y=1)\mathbb{P}(y=1)}{\mathbb{P}(\mathbf{x}|y=0)\mathbb{P}(y=0)}\\ & =-\frac{1}{2}(\mathbf{x}-{\mu }_1{)}^T{\mathbf{\Sigma }}^{-1}(\mathbf{x}-{\mu }_1)+\frac{1}{2}(\mathbf{x}-{\mu }_0{)}^T{\mathbf{\Sigma }}^{-1}(\mathbf{x}-{\mu }_0)+\ln \frac{\mathbb{P}(y=1)}{\mathbb{P}(y=0)}\\ & =({\mu }_1-{\mu }_0{)}^T{\mathbf{\Sigma }}^{-1}\mathbf{x}-\frac{1}{2}{\mu }_1^T{\mathbf{\Sigma }}^{-1}{\mu }_1+\frac{1}{2}{\mu }_0^T{\mathbf{\Sigma }}^{-1}{\mu }_0+\ln \frac{\mathbb{P}(y=1)}{\mathbb{P}(y=0)}\end{array}$$
其中先验概率 $\mathbb{P}(y=1)$ 和 $\mathbb{P}(y=0)$ 是常数，上式可简化为
$$z={\mathbf{w}}^T\mathbf{x}+b$$
于是
$$\mathbb{P}(y=1|\mathbf{x})=\frac{1}{1+e^{-z}}$$
上式称为 Sigmoid 函数（S型曲线），也称 logistic 函数。

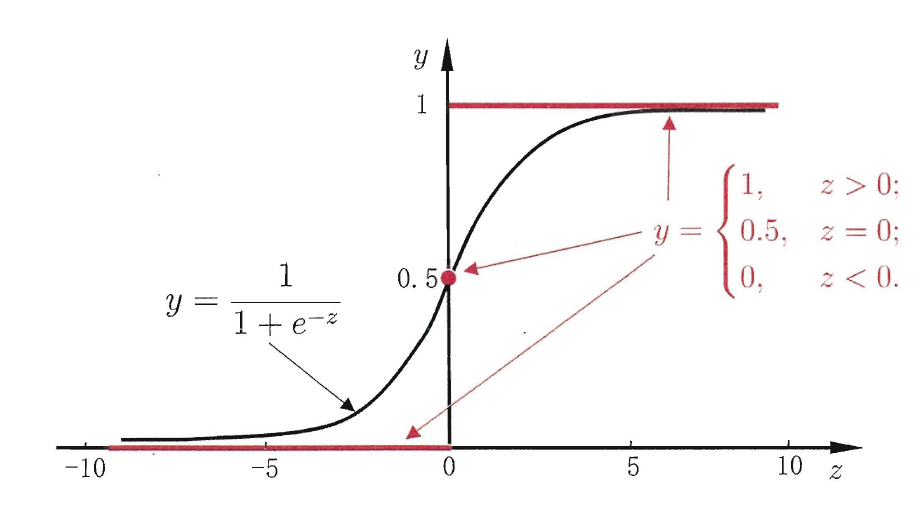
Model: 逻辑回归 (logistic regression, logit regression) 通过引入Sigmod 函数将输入值映射到 $[0,1]$ 来实现分类功能。
$$f_{\mathbf{w},b}(\mathbf{x})=g({\mathbf{w}}^T\mathbf{x}+b)$$
其中
$$g(z)=\frac{1}{1+e^{-z}}$$
式中特征向量 $\mathbf{x}=(x_1,x_2,\cdots ,x_p{)}^T$，参数 $\mathbf{w}=(w_1,w_2,\cdots ,w_p{)}^T$ 称为系数 (coefficients) 或权重 (weights)，标量 $b$ 称为偏置项(bias) 。

为计算方便，模型简写为
$$f_{\mathbf{w}}(\mathbf{x})=\frac{1}{1+\exp (-{\mathbf{w}}^T\mathbf{x})}$$
其中，特征向量 $\mathbf{x}=(1,x_1,x_2,\cdots ,x_p{)}^T$，权重向量 $\mathbf{w}=(b,w_1,w_2,\cdots ,w_p{)}^T$

可以通过引入阈值（默认0.5）实现分类预测
$$\hat{y}=\{\begin{array}{ll}1& \text{if }{f}_{\mathbf{w}}(\mathbf{x})⩾0.5\\ 0& \text{if }{f}_{\mathbf{w}}(\mathbf{x})<0.5\end{array}$$
模型的输出为正样本的概率
$$\{\begin{array}{l}\mathbb{P}(y=1|\mathbf{x})=f_{\mathbf{w}}(\mathbf{x})\\ \mathbb{P}(y=0|\mathbf{x})=1-f_{\mathbf{w}}(\mathbf{x})\end{array}$$

可简记为
$$\mathbb{P}(y|\mathbf{x})=[f_{\mathbf{w}}(\mathbf{x}){]}^y[1-f_{\mathbf{w}}(\mathbf{x}){]}^{1-y}$$

极大似然估计

logistic 回归若采用均方误差作为 cost function，是一个非凸函数(non-convex)，会存在许多局部极小值，因此我们尝试极大似然估计。

极大似然估计：(maximum likelihood estimate, MLE) 使得观测样本出现的概率最大，也即使得样本联合概率（也称似然函数）取得最大值。

为求解方便，对样本联合概率取对数似然函数
$$\begin{array}{rl}\log L(\mathbf{w})& =\log \prod _{i=1}^N\mathbb{P}(y_i|{\mathbf{x}}_i)=\sum _{i=1}^N\log \mathbb{P}(y_i|{\mathbf{x}}_i)\\ & =\sum _{i=1}^N[y_i\log f_{\mathbf{w}}({\mathbf{x}}_i)+(1-y_i)\log (1-f_{\mathbf{w}}({\mathbf{x}}_i))]\end{array}$$
因此，可定义 loss function
$$\begin{array}{rl}L(f_{\mathbf{w}}(\mathbf{x}),y)& =-y\log f_{\mathbf{w}}(\mathbf{x})-(1-y)\log (1-f_{\mathbf{w}}(\mathbf{x}))\\ & =-y{\mathbf{w}}^T\mathbf{x}+\log (1+e^{{\mathbf{w}}^T\mathbf{x}})\end{array}$$

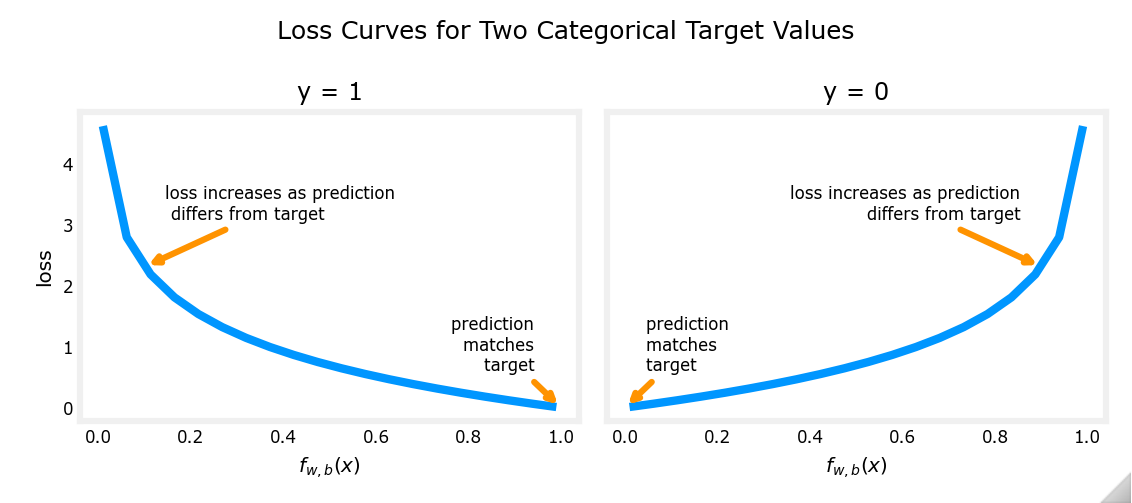
最大化似然函数等价于最小化 cost function
$$J(\mathbf{w})=\frac{1}{N}\sum _{i=1}^N(-y_i{\mathbf{w}}^T\mathbf{x}+\log (1+e^{{\mathbf{w}}^T\mathbf{x}}))$$
参数估计 ：(parameter estimation) $J(\mathbf{w})$ 是关于参数 $\mathbf{w}$ 的高阶可导连续凸函数，经典的数值优化算法如梯度下降法 (gradient descent method) 、牛顿法 (Newton method) 等都可求得其最优解
$$\arg \underset{\mathbf{w}}{\min }J(\mathbf{w})$$

最大期望算法

最大期望算法：（Expectation-Maximization algorithm, EM）与真实分布最接近的模拟分布即为最优分布，因此可以通过最小化交叉熵来求出最优分布。

对任意样本 $({\mathbf{x}}_i,y_i)$，真实分布可写为（真实分布当然完美预测）
$$\mathbb{P}(y_i|{\mathbf{x}}_i)=1$$
模拟分布可写为
$$\mathbb{Q}(y_i|{\mathbf{x}}_i)=[f_{\mathbf{w}}({\mathbf{x}}_i){]}^y[1-f_{\mathbf{w}}({\mathbf{x}}_i){]}^{1-y}$$
交叉熵为
$$\begin{array}{rl}H(\mathbb{P},\mathbb{Q})& =-\sum _{i=1}^N\mathbb{P}(y_i|{\mathbf{x}}_i)\log \mathbb{Q}(y_i|{\mathbf{x}}_i)\\ & =\sum _{i=1}^N(-y_i{\mathbf{w}}^T\mathbf{x}+\log (1+e^{{\mathbf{w}}^T\mathbf{x}}))\end{array}$$
cost function
$$J(\mathbf{w})=\frac{1}{N}\sum _{i=1}^N(-y_i{\mathbf{w}}^T\mathbf{x}+\log (1+e^{{\mathbf{w}}^T\mathbf{x}}))$$
与极大似然估计相同。

决策边界

决策边界：逻辑回归模型 $f_{\mathbf{w},b}(\mathbf{x})=g(z)=g({\mathbf{w}}^T\mathbf{x}+b)$

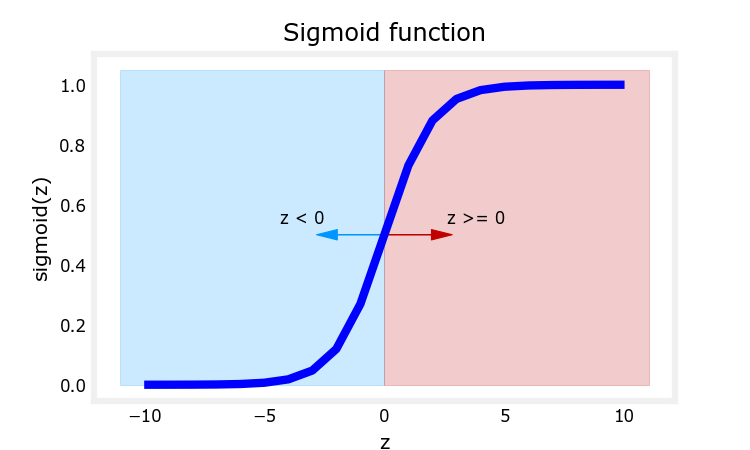
在 logistic 回归模型中，$z={\mathbf{w}}^T\mathbf{x}+b$ 。对于 sigmoid 函数（如上图），$g(z)⩾0.5\text{ for }z⩾0$ 。因此，模型预测
$$\hat{y}=\{\begin{array}{ll}1& \text{if }{\mathbf{w}}^T\mathbf{x}+b⩾0\\ 0& \text{if }{\mathbf{w}}^T\mathbf{x}+b<0\end{array}$$
由此可见，logistic 回归输出一个线性决策边界 (linear decision boundary)
$${\mathbf{w}}^T\mathbf{x}+b=0$$
我们也可以创建多项式特征拟合一个非线性边界。例如，模型
$f(x_1,x_2)=g(x_1^2+x_2^2-36)\text{ where }g(z)=\frac{1}{1+e^{-z}}$
决策边界方程为 $x_1^2+x_2^2-36=0$

Softmax 回归

基本形式

Softmax 回归是 Logistic 回归在多分类（Multi-Class）问题上的推广。给定的数据集
$$D=\{({\mathbf{x}}_1,y_1),({\mathbf{x}}_2,y_2),\cdots ,({\mathbf{x}}_N,y_N\}$$
包含 $N$ 个样本，$p$ 个特征。其中，第 $i$ 个样本的特征向量为 ${\mathbf{x}}_i=(x_{i1},x_{i2},\cdots ,x_{ip}{)}^T$ 。目标变量 y i ∈ { c 1 , c 2 , ⋯   , c K } y_i\in \{c_1,c_2,\cdots,c_K\} yi​∈{c1​,c2​,⋯,cK​}​ 。假设$K$个类的数据集服从均值不同、方差相同的正态分布
$$\mathbb{P}(\mathbf{x}|y=c_k)=\frac{1}{\sqrt{(2\pi {)}^p\det \mathbf{\Sigma }}}\exp \left(-\frac{1}{2}(\mathbf{x}-{\mu }_k{)}^T{\mathbf{\Sigma }}^{-1}(\mathbf{x}-{\mu }_k)\right),k=1,2,\cdots ,K$$
其中，协方差矩阵$\mathbf{\Sigma }$ 为对称阵。利用贝叶斯定理，于类别 $c_k$ 的条件概率为
$$\mathbb{P}(y=c_k|\mathbf{x})=\frac{\mathbb{P}(\mathbf{x}|y=c_k)\mathbb{P}(y=c_k)}{{\sum }_{s=1}^K\mathbb{P}(\mathbf{x}|y=c_s)\mathbb{P}(y=c_s)}$$
参考Logistic 回归，计算[^cdot]
$$\begin{array}{rl}\varphi & =\ln \frac{\mathbb{P}(\mathbf{x}|y=c_s)\mathbb{P}(y=c_s)}{\mathbb{P}(\mathbf{x}|y=c_t)\mathbb{P}(y=c_t)}\\ & =-\frac{1}{2}(\mathbf{x}-{\mu }_s{)}^T{\mathbf{\Sigma }}^{-1}(\mathbf{x}-{\mu }_s)+\frac{1}{2}(\mathbf{x}-{\mu }_t{)}^T{\mathbf{\Sigma }}^{-1}(\mathbf{x}-{\mu }_t)+\ln \frac{\mathbb{P}(y=c_s)}{\mathbb{P}(y=c_t)}\\ & =({\mu }_s-{\mu }_t{)}^T{\mathbf{\Sigma }}^{-1}\mathbf{x}-\frac{1}{2}({\mu }_s^T{\mathbf{\Sigma }}^{-1}{\mu }_s-{\mu }_t^T{\mathbf{\Sigma }}^{-1}{\mu }_t)+\ln \mathbb{P}(y=c_s)-\ln \mathbb{P}(y=c_t)\\ & =({\mathbf{w}}_s^T\mathbf{x}+b_s)-({\mathbf{w}}_t^T\mathbf{x}+b_t)\end{array}$$
其中
$${\mathbf{w}}_k^T={\mu }_k^T{\mathbf{\Sigma }}^{-1},b_k=-\frac{1}{2}{\mu }_k^T{\mathbf{\Sigma }}^{-1}{\mu }_k+\ln \mathbb{P}(y=c_k)$$
记 $z_k={\mathbf{w}}_k^T\mathbf{x}+b_k$，则后验概率
$$\begin{array}{rl}\mathbb{P}(y=c_k|\mathbf{x})& =\frac{1}{\sum _{s=1}^K\frac{\mathbb{P}(\mathbf{x}|y=c_s)\mathbb{P}(y=c_s)}{\mathbb{P}(\mathbf{x}|y=c_k)\mathbb{P}(y=c_k)}}\\ & =\frac{1}{{\sum }_{s=1}^K\exp (z_s-z_k)}\\ & =\frac{\exp (z_k)}{{\sum }_{s=1}^K\exp (z_s)}\end{array}$$
类别 $c_k$ 的条件概率可化简为
$$\mathbb{P}(y=c_k|\mathbf{x})=\text{softmax}({\mathbf{w}}_k^T\mathbf{x})=\frac{\exp ({\mathbf{w}}_k^T\mathbf{x})}{{\sum }_{k=1}^K\exp ({\mathbf{w}}_k^T\mathbf{x})}$$
其中，参数 ${\mathbf{w}}_{\mathbf{k}}=(b_k,w_{k1},w_{k2},\cdots ,w_{kp}{)}^T$ 是类别 $c_k$ 的权重向量，特征向量 $\mathbf{x}=(1,x_1,x_2,\cdots ,x_p{)}^T$。

Model: Softmax 回归输出每个类别的概率
$$\mathbf{f}(\mathbf{x};\mathbf{W})=\frac{1}{{\sum }_{k=1}^K\exp ({\mathbf{w}}_k^T\mathbf{x})}\left(\begin{array}{c}\exp ({\mathbf{w}}_1^T\mathbf{x})\\ \exp ({\mathbf{w}}_2^T\mathbf{x})\\ ⋮\\ \exp ({\mathbf{w}}_K^T\mathbf{x})\end{array}\right)$$
上式结果向量中最大值的对应类别为最终类别
$$\hat{y}=\arg \underset{c_k}{\max }{\mathbf{w}}_k^T\mathbf{x}$$

极大似然估计

为了方便起见，我们用 $K$ 维的 one-hot 向量来表示类别标签。若第 $i$ 个样本类别为 $c$，则向量表示为
$$\begin{array}{rl}{\mathbf{y}}_i& =(y_{i1},y_{i2},\cdots ,y_{iK}{)}^T\\ & =(\mathbb{I}(c_1=c),\mathbb{I}(c_2=c),\cdots ,\mathbb{I}(c_K=c){)}^T\end{array}$$
对样本联合概率取对数似然函数
$$\begin{array}{rl}\log L(\mathbf{W})& =\log \prod _{i=1}^N\mathbb{P}(y_i|{\mathbf{x}}_i)=\sum _{i=1}^N\log \mathbb{P}(y_i|{\mathbf{x}}_i)\\ & =\sum _{i=1}^N\log {\mathbf{y}}_i^T\mathbf{f}({\mathbf{x}}_i;\mathbf{W})\end{array}$$
参数估计：可通过梯度下降法、牛顿法等求解$K\times (p+1)$权重矩阵 $\mathbf{W}$
$$\hat{\mathbf{W}}=\arg \underset{\mathbf{W}}{\max }\sum _{i=1}^N\log {\mathbf{y}}_i^T\mathbf{f}({\mathbf{x}}_i;\mathbf{W})$$
对数似然函数 $\log L(\mathbf{W})$ 关于$\mathbf{W}$ 的梯度为
$$\frac{\partial \log L(\mathbf{W})}{\partial \mathbf{W}}=\sum _{i=1}^N{\mathbf{x}}_i({\mathbf{y}}_i-\mathbf{f}({\mathbf{x}}_i;\mathbf{W}){)}^T$$

感知机

感知机（Perceptron）是线性二分类模型，适用于线性可分的数据集。

Model：感知机选取符号函数为激活函数
$$f_{\mathbf{w},b}(\mathbf{x})=\text{sign}({\mathbf{w}}^T\mathbf{x}+b)$$
这样就可以将线性回归的结果映射到两分类的结果上了。符号函数
$$\text{sign}(z)=\{\begin{array}{ll}+1& \text{if }z⩾0\\ -1& \text{if }z<0\end{array}$$
为计算方便，引入 $x_0=1,w_0=b$ 。模型简写为
$$f_{\mathbf{w}}(\mathbf{x})=\text{sign}({\mathbf{w}}^T\mathbf{x})$$
其中，特征向量 $\mathbf{x}=(x_0,x_1,x_2,\cdots ,x_p{)}^T$，权重向量 $\mathbf{w}=(w_0,w_1,w_2,\cdots ,w_p{)}^T$

cost function：误分类点到分离超平面的总距离
$$J(\mathbf{w})=-\sum _{{\mathbf{x}}_i\in M}{y}_i{\mathbf{w}}^T{\mathbf{x}}_i$$
其中，$M$ 是错误分类集合。

基于梯度下降法对代价函数的最优化算法，有原始形式和对偶形式。算法简单且易于实现。

损失函数的梯度
$$\nabla J(\mathbf{w})=-\sum _{{\mathbf{x}}_i\in M}{y}_i{\mathbf{x}}_i$$

感知机有无穷多个解，其解由于不同的初始值或不同的迭代顺序而有所不同。

Perceptron 是另一种适用于大规模学习的简单分类算法。

• 它不需要设置学习率
• 它不需要正则项
• 它只用错误样本更新模型

最后一个特点意味着Perceptron的训练速度略快于带有合页损失(hinge loss)的SGD，因此得到的模型更稀疏。

被动感知算法 (Passive Aggressive Algorithms) 是一种大规模学习的算法。和感知机相似，因为它们不需要设置学习率。然而，与感知器不同的是，它们包含正则化参数。

多类别分类

Multi-class classification：目标变量包含两个以上离散值的分类任务 y ∈ { c 1 , c 2 , ⋯   , c K } y\in\{c_1,c_2,\cdots,c_K\} y∈{c1​,c2​,⋯,cK​}。每个样本只能标记为一个类。例如，使用从一组水果图像中提取的特征进行分类，其中每一幅图像都可能是一个橙子、一个苹果或一个梨。每个图像就是一个样本，并被标记为三个可能的类之一。

• One-Vs-Rest (OVR) 也称为one-vs-all，为每个类分别拟合一个二分类模型，这是最常用的策略，对每个类都是公平的。这种方法的一个优点是它的可解释性，每个类都可以查看自己模型的相关信息。

• One-Vs-One (OVO) 是对每一对类分别拟合一个二分类模型。在预测时，选择得票最多的类别。在票数相等的两个类别中，它选择具有最高总分类置信度的类别，方法是对由底层二分类器计算的对分类置信度进行求和。

  由于它需要拟合 $\frac{K(K-1)}{2}$ 个分类器，这种方法通常比one-vs-rest要慢，原因就在于其复杂度 O(K²) 。然而，这个方法也有优点，比如说是在没有很好的缩放样本数的核方法中。这是因为每个单独的学习问题只涉及一小部分数据，而对于一个 one-vs-rest，完整的数据集将会被使用 K 次。

One-Vs-Rest：为每个类分别拟合一个二分类模型
$$f_{\mathbf{w},b}^i(\mathbf{x})=\mathbb{P}(y=i|\mathbf{x};\mathbf{w},b)$$
模型预测值，一种方法是选择概率最大的类别
$$\hat{y}=\arg \underset{i}{\max }{f}_{\mathbf{w},b}^i(\mathbf{x})$$

多标签分类

包含多个目标变量的分类任务称为 Multilabel classification