【学习笔记】数据结构（三）

栈和队列

文章目录

栈和队列
- 3.1 栈 - Stack
- - 3.1.1 抽象数据类型栈的定义
  - 3.1.2 栈的表示和实现
- 3.2 栈的应用举例
- - 3.2.1 数制转换
  - 3.2.2 括号匹配的检验
  - 3.2.3 迷宫求解
  - 3.2.4 表达式求值 - 波兰、逆波兰
  - 3.2.5 反转一个字符串或者反转一个链表
- 3.3 栈与递归的实现
- 3.4 队列 - Queue
- - 3.4.1 抽象数据类型队列的定义
  - 3.4.2 链队列--队列的链式表示和实现
  - 3.4.3 循环队列--队列的顺序表示和实现

3.1 栈 - Stack

3.1.1 抽象数据类型栈的定义

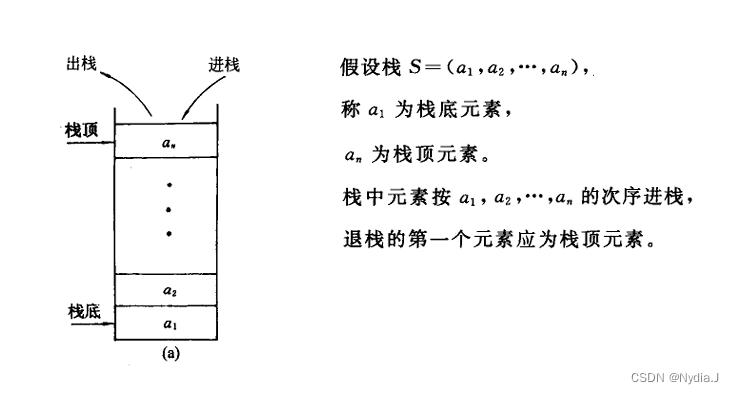
栈(stack)是限定仅在表尾进行插人或删除操作的线性表。栈又称为后进先出(last in first out)的线性表(简称 LIFO 结构)。

表尾端称为栈顶(top)，表头端称为栈底(bottom)。

不含元素的空表称为空栈。

在这里插入图片描述

栈的抽象数据类型的定义：

在这里插入图片描述

3.1.2 栈的表示和实现

顺序栈 , 即栈的顺序存储结构是利用一组地址连续的存储单元依次存放自栈底到栈顶的数据元素，同时附设指针top指示栈顶元素在顺序栈中的位置。通常的top=0表示空栈。

由于栈在使用过程中所需最大空间的大小很难估计，因此,一般来说,在初始化设空栈时不应限定栈的最大容量。一个较合理的做法是:先为栈分配一个基本容量,然后在应用过程中,当栈的空间不够使用时再逐段扩大。为此,可设定两个常量：STACK_INIT_SIZE(存储空间初始分配量)和STACKINCREMENT(存储空间分配增量)。
typedef struct {
	SElemType * base;
	SElemType * top;
	int stacksize; //指示栈的当前可使用的最大容量
}SqStack;

栈的初始化操作为：

按设定的初始分配量进行第一次存储分配；
称base为栈底指针, 在顺序栈中,它始终指向栈底的位置, 若base的值为 NULL, 则表明栈结构不存在。
称top为栈顶指针,其初值指向栈底,即top=base可作为栈空的标记，每当插人新的栈顶元素时，指针top增1；删除栈顶元素时，指针top减1，因此，非空栈中的栈顶指针始终在栈顶元素的下一个位置上。

在这里插入图片描述

#define _CRT_SECURE_NO_WARNINGS *1
#include <stdio.h>
#include <stdlib.h>

#define STACK_INIT_SIZE 100 //存储空间初始分配量
#define STACKINCREMENT 10 //存储空间分配增量

#define OK 1 //完成
#define OVERFLOW -1 //失败
#define ERROR -2 //错误

typedef int Status;
typedef struct {
	int* base; // 在栈构造之前和销毁之后，base的值为NULL
	int* top; // 栈顶指针
	int stacksize; //指示栈的当前可使用的最大容量
}SqStack;

Status InitStack(SqStack* S) {
	// 构造一个空栈S
	S->base = (int*) malloc(STACK_INIT_SIZE * sizeof(int));
	if (!S->base) exit(OVERFLOW);
	S->top = S->base;
	S->stacksize = STACK_INIT_SIZE;
	return OK;
}

Status Push(SqStack* S, int e) {
	// 插入元素 e为新的栈顶元素
	if (S->top - S->base >= S->stacksize) { //栈满，追加存储空间
		S->base = (int*)realloc(S->base, (S->stacksize + STACKINCREMENT) * sizeof(int));
		if (!S->base) exit(OVERFLOW);
		S->top = S->base + S->stacksize;
		S->stacksize += STACKINCREMENT;
	}
	*S->top++ = e;
	return OK;
}

Status Pop(SqStack* S, int* e) {
	// 若栈不空,则删除s的栈顶元素,用e返回其值,并返回OK;否则返回 ERROR
	if (S->top == S->base) return ERROR;
	*e = *--S->top;
	return OK;
}

Status GetTop(SqStack S, int* e) {
	// 若栈不空, 则用e返回s的栈顶元素, 并返回0K; 否则返回ERROR
	if (S.top == S.base) return ERROR;
	*e = *(S.top - 1);
	return OK;
}

Status DestroyStack(SqStack* S) {
	// 销毁栈S
	free(S->base);
	S->base = NULL;
	S->top = NULL;
	S->stacksize = 0;
	return OK;
}

int main() {
	SqStack S;
	if (InitStack(&S) != OK) {
		printf("Stack initialization failed.\n");
		return OVERFLOW;
	}
	int e; // 使用一个整数变量而不是指针
	Push(&S, 1);
	Push(&S, 2);
	Push(&S, 3);
	Push(&S, 4);
	Status status = Pop(&S, &e);
	if (status == OK) {
		// 删除的元素
		printf("Popped element: %d\n", e);
	}
	else {
		printf("Error: Stack is empty.\n");
	}
	if (GetTop(S, &e) == OK) {
		// 此时栈顶的元素
		printf("Top element: %d\n", e);
	}
	DestroyStack(&S);
	return 0;
}

使用数组实现一个栈

#define _CRT_SECURE_NO_WARNINGS *1
#include <stdio.h>
#include <stdlib.h>

#define MAX_SIZE 101
int A[MAX_SIZE];
int top = -1;

void Push(int x)
{
	if (top == MAX_SIZE - 1)
	{
		printf("Error:stack overflow\n"); 
		return;
	}
	A[++top] = x;
}

void Pop() {
	if (top == -1) {
		printf("Error: No element to pop\n");
		return;
	}
	top--;
}

int Top()
{
	if (top != -1)
	{
		return A[top];
	}	
}

void Print()
{
	int i;
	printf("Stack: ");
	for (i = 0; i <= top; i++) {
		printf("%d ", A[i]);
	}
	printf("\n");
}

int main() {
	Push(2); Print(); 
	Push(5); Print(); 
	Push(10); Print(); 
	Pop(); Print(); 
	Push(12); Print();
	return 0;
}

使用链表实现一个栈

#define _CRT_SECURE_NO_WARNINGS *1
#include <stdio.h>
#include <stdlib.h>
#include <stdbool.h>
 
typedef struct Node {
	int data;
	struct Node* link;
}Node;
struct Node* top;

void Push(int x) {
	Node* temp = (Node*)malloc(sizeof(Node));
	temp->data = x;
	temp->link = top;
	top = temp;
}

void Pop() {
	Node* temp;
	if (top == NULL) return;
	temp = top;
	top = top->link;
	free(temp);
}

int Top() {
	return top->data;
}

bool IsEmpty() {
	if (top == NULL) {
		return true;
	}
	return false;
}

void Print() {
	Node* temp = top;
	printf("List: ");
	while (temp != NULL) {
		printf("%d ", temp->data);
		temp = temp->link;
	}
	printf("\n");
}

int main() {
	top = NULL;
	printf("%d \n", IsEmpty());
	Push(2);
	Push(4);
	Push(1);
	Print();
	Pop();
	Print();
	printf("%d \n", Top());
	printf("%d \n", IsEmpty());
	return 0;
}

3.2 栈的应用举例

3.2.1 数制转换

十进制数N和其他d进制数的转换
$\text{ div } d) \times d + N \bmod d \text{ (其中：div为整除运算，mod为求余运算)}$
在这里插入图片描述

#define _CRT_SECURE_NO_WARNINGS *1
#include <stdio.h>
#include <stdlib.h>

#define STACK_INIT_SIZE 100 //存储空间初始分配量
#define STACKINCREMENT 10 //存储空间分配增量

#define OK 1 //完成
#define OVERFLOW -1 //失败
#define ERROR -2 //错误

typedef int Status;
typedef struct {
	int* base; // 在栈构造之前和销毁之后，base的值为NULL
	int* top; // 栈顶指针
	int stacksize; //指示栈的当前可使用的最大容量
}SqStack;

Status InitStack(SqStack* S) {
	// 构造一个空栈S
	S->base = (int*) malloc(STACK_INIT_SIZE * sizeof(int));
	if (!S->base) exit(OVERFLOW);
	S->top = S->base;
	S->stacksize = STACK_INIT_SIZE;
	return OK;
}

Status StackEmpty(SqStack S) {
	return (S.top == S.base) ? OK : ERROR;
}

Status Push(SqStack* S, int e) {
	// 插入元素 e为新的栈顶元素
	if (S->top - S->base >= S->stacksize) { //栈满，追加存储空间
		S->base = (int*)realloc(S->base, (S->stacksize + STACKINCREMENT) * sizeof(int));
		if (!S->base) exit(OVERFLOW);
		S->top = S->base + S->stacksize;
		S->stacksize += STACKINCREMENT;
	}
	*S->top++ = e;
	return OK;
}

Status Pop(SqStack* S, int* e) {
	// 若栈不空,则删除s的栈顶元素,用e返回其值,并返回OK;否则返回 ERROR
	if (S->top == S->base) return ERROR;
	*e = *--S->top;
	return OK;
}

Status GetTop(SqStack S, int* e) {
	// 若栈不空, 则用e返回s的栈顶元素, 并返回0K; 否则返回ERROR
	if (S.top == S.base) return ERROR;
	*e = *(S.top - 1);
	return OK;
}

Status DestroyStack(SqStack* S) {
	// 销毁栈S
	free(S->base);
	S->base = NULL;
	S->top = NULL;
	S->stacksize = 0;
	return OK;
}

void conversion() {
	SqStack S;
	if (InitStack(&S) != OK) {
		printf("Stack initialization failed.\n");
	}
	int e, N;
	printf("请输入一个十进制数：");
	int num = scanf("%d", &N);
	if (num == 1) {
		while (N) {
			Push(&S, N % 8);
			N = N / 8;
		}
		while (StackEmpty(S) != OK) {
			Pop(&S, &e);
			printf("%d", e);
		}
		DestroyStack(&S);
	}
	
}

int main() {
	conversion();
	return 0;
}

3.2.2 括号匹配的检验

算法的设计思想:

凡出现左括弧，则进栈;

凡出现右括弧，首先检查栈是否空；

若栈空，则表明“右括弧”多了
否则和栈顶元素比较
若相匹配，则“左括弧出栈”
否则不匹配

表达式检验结束时

若栈空，则匹配正确

否则表明“左括弧”多了

#define _CRT_SECURE_NO_WARNINGS *1
#include <stdio.h>
#include <stdlib.h>

#define OVERFLOW -1

#define STACK_INIT_SIZE 100 //存储空间初始分配量
#define STACKINCREMENT 10 //存储空间分配增量

typedef struct {
    char* base;
    char* top;
    int stackSize;
} Stack;

void InitStack(Stack* s) {
    s->base = (char*)malloc(100 * sizeof(char));
    if (!s->base) exit(1); // 分配内存失败
    s->top = s->base;
    s->stackSize = STACK_INIT_SIZE;
}

void Push(Stack* s, char elem) {
    if (s->top - s->base >= s->stackSize) { // 栈满，需要扩容
        s->base = (char*)realloc(s->base, (s->stackSize + STACKINCREMENT) * sizeof(char));
        if (!s->base) exit(OVERFLOW); // 扩容失败
        s->top = s->base + s->stackSize;
        s->stackSize += STACKINCREMENT;
    }
    *(s->top++) = elem;
}

char Pop(Stack* s) {
    if (s->top == s->base) return '\0'; // 栈空
    return *(--s->top);
}

int StackEmpty(Stack s) {
    return s.top == s.base;
}

void DestroyStack(Stack* s) {
    free(s->base);
    s->base = NULL;
    s->top = NULL;
    s->stackSize = 0;
}

int CheckBrackets(const char* str) {
    Stack s;
    InitStack(&s);
    char c, topChar;

    while (*str) {
        switch (*str) {
        case '(':
        case '[':
        case '{':
            Push(&s, *str);
            break;
        case ')':
        case ']':
        case '}':
            if (StackEmpty(s)) {
                DestroyStack(&s);
                return 0; // 没有匹配的左括号
            }
            topChar = Pop(&s);
            if ((topChar == '(' && *str != ')') ||
                (topChar == '[' && *str != ']') ||
                (topChar == '{' && *str != '}')) {
                DestroyStack(&s);
                return 0; // 括号不匹配
            }
            break;
        }
        str++;
    }

    int isEmpty = StackEmpty(s);
    DestroyStack(&s);
    return isEmpty; // 如果栈为空，所有括号正确匹配
}

int main() {
    char expression[100];
    printf("Enter an expression: ");
    scanf("%99s", expression);

    if (CheckBrackets(expression)) {
        printf("The brackets are correctly matched.\n");
    }
    else {
        printf("The brackets are not matched.\n");
    }

    return 0;
}

3.2.3 迷宫求解

迷宫路径算法的基本思想是:

若当前位置“可通”，则纳入路径继续前进
若当前位置“不可通”，则后退,换向探索
若四周均“不可通”，则从路径中删除

#define _CRT_SECURE_NO_WARNINGS *1
#include <stdio.h>
#include <stdlib.h>

#define MAXSIZE 100  // 堆栈最大容量
#define MAZE_SIZE 5  // 迷宫大小

#define OK 1 //完成
#define OVERFLOW -1 //失败
#define ERROR -2 //错误

typedef struct {
    int x;
    int y;
} PosType;

typedef struct {
    int ord;  // 通道块在路径上的序号
    PosType seat; // 通道块在迷宫中的坐标位置
    int di; // 从此通道块走向下一通道块的方向
} SElemType; // 栈的元素类型

typedef struct {
    SElemType* base;
    SElemType* top;
    int stacksize;
} Stack;

typedef int Status;
typedef int MazeType[MAZE_SIZE][MAZE_SIZE];


void InitStack(Stack* S) {
    S->base = (SElemType*)malloc(MAXSIZE * sizeof(SElemType));
    if (!S->base) exit(ERROR);
    S->top = S->base;
    S->stacksize = MAXSIZE;
}

Status Push(Stack* S, SElemType e) {
    if (S->top - S->base >= S->stacksize) {
        S->base = (SElemType*)realloc(S->base, (S->stacksize + 10) * sizeof(SElemType));
        if (!S->base) exit(ERROR);
        S->top = S->base + S->stacksize;
        S->stacksize += 10;
    }
    *S->top++ = e;
    return OK;
}


Status Pop(Stack* S, SElemType* e) {
    if (S->top == S->base) return ERROR;
    *e = *--S->top;
    return OK;
}

Status StackEmpty(Stack s) {
    return s.top == s.base;
}

// 检查当前位置是否可以通过
Status Pass(MazeType maze, PosType curpos) {
    // 检查坐标是否在迷宫范围内
    if (curpos.x < 0 || curpos.x >= MAZE_SIZE || curpos.y < 0 || curpos.y >= MAZE_SIZE) {
        return ERROR;  // 超出边界，不可通过
    }
    return maze[curpos.x][curpos.y] == 0;  // 返回1如果是通道，0如果是墙或已访问
}

// 留下足迹，标记位置已访问
Status FootPrint(MazeType maze, PosType curpos) {
    // 检查坐标是否在迷宫范围内
    if (curpos.x >= 0 && curpos.x < MAZE_SIZE && curpos.y >= 0 && curpos.y < MAZE_SIZE) {
        maze[curpos.x][curpos.y] = -1;  // 使用-1标记已访问
    }
}

// 标记位置为死胡同
void MarkPrint(MazeType maze, PosType pos) {
    // 检查坐标是否在迷宫范围内
    if (pos.x >= 0 && pos.x < MAZE_SIZE && pos.y >= 0 && pos.y < MAZE_SIZE) {
        maze[pos.x][pos.y] = 2;  // 使用2标记为死胡同
    }
}

PosType NextPos(PosType pos, int di) {
    PosType next = pos;
    switch (di) {
    case 1: next.y++; break;  // 向东
    case 2: next.x++; break;  // 向南
    case 3: next.y--; break;  // 向西
    case 4: next.x--; break;  // 向北
    }
    return next;
}

Status MazePath(MazeType maze, PosType start, PosType end) {
    // 若迷宫 maze 中存在从入口 start 到出口 end 的通道，则求得一条存放在栈中（从栈底到栈顶），并返回 TRUE; 否则返回 FALSE
    Stack s;
    InitStack(&s);
    PosType curpos = start; // 设定“当前位置”为“入口位置”
    int curstep = 1; // 探索第一步
    SElemType pop_elem;
    do {
        if (Pass(maze, curpos) == 1) { // 当前位置可以通过，即是未曾走到过的通道块
            FootPrint(maze, curpos); // 留下足迹
            SElemType e = { curstep, curpos, 1 };
            Push(&s, e); //  加入路径
            if (curpos.x == end.x && curpos.y == end.y) //  到达终点（出口）
                return OK;
            curpos = NextPos(curpos, 1);// 下一位置是当前位置的东邻
            curstep++;// 探索下一步
        }
        else { // 当前位置不能通过
            if (!StackEmpty(s)) {
                Pop(&s, &pop_elem);
                while (pop_elem.di == 4 && !StackEmpty(s)) {
                    MarkPrint(maze, pop_elem.seat); // 留下不能通过的标记，并退回一步
                    Pop(&s, &pop_elem);
                }
                if (pop_elem.di < 4) {
                    pop_elem.di++;
                    Push(&s, pop_elem); // 换下一个方向探索
                    curpos = NextPos(pop_elem.seat, pop_elem.di); // 设定当前位置是该新方向上的相邻块
                }
            }
        }
    } while (!StackEmpty(s));
}

int main() {
    MazeType maze = {
        {0, 1, 0, 0, 0},
        {0, 1, 1, 1, 0},
        {0, 0, 0, 1, 0},
        {0, 1, 0, 0, 0},
        {0, 0, 0, 1, 0}
    };
    PosType start = { 0, 0 };
    PosType end = { 4, 4 };
    MazePath(maze, start, end);
    printf("\nAfter MarkPrint:\n");
    for (int i = 0; i < MAZE_SIZE; i++) {
        for (int j = 0; j < MAZE_SIZE; j++) {
            if (maze[i][j] == -1) {
                printf("(%d,%d) ", i, j);
            }
        }
        printf("\n");
    }
    return 0;
}

3.2.4 表达式求值 - 波兰、逆波兰

//10以内计算
#define _CRT_SECURE_NO_WARNINGS *1
#include <stdio.h>
#include <stdlib.h>

#define OK 1 // 完成
#define OVERFLOW -1 // 失败
#define ERROR -2 // 错误
#define INF 1e9 // 不合法

#define STACK_INIT_SIZE 100 //存储空间初始分配量
#define STACKINCREMENT 10 //存储空间分配增量

typedef char SElemType;
typedef int Status;
typedef struct {
    SElemType* base;
    SElemType* top;
    int stackSize;
}Stack;

Status InitStack(Stack* S) {
    // 构造一个空栈S
    S->base = (SElemType*)malloc(STACK_INIT_SIZE * sizeof(SElemType));
    if (!S->base) exit(OVERFLOW);
    S->top = S->base;
    S->stackSize = STACK_INIT_SIZE;
    return OK;
}

Status Push(Stack* S, char e) {
    // 插入元素 e为新的栈顶元素
    if (S->top - S->base >= S->stackSize) { //栈满，追加存储空间
        S->base = (SElemType*)realloc(S->base, (S->stackSize + STACKINCREMENT) * sizeof(SElemType));
        if (!S->base) exit(OVERFLOW);
        S->top = S->base + S->stackSize;
        S->stackSize += STACKINCREMENT;
    }
    *S->top++ = e;
    return OK;
}

Status Pop(Stack* S, char* e) {
    // 若栈不空,则删除s的栈顶元素,用e返回其值,并返回OK;否则返回 ERROR
    if (S->top == S->base) return ERROR;
    *e = *--S->top;
    return OK;
}

Status DestroyStack(Stack* S) {
    // 销毁栈S
    free(S->base);
    S->base = NULL;
    S->top = NULL;
    S->stackSize = 0;
    return OK;
}

char GetTop(Stack S) {
    if (S.top == S.base) return ERROR;
    SElemType e = *(S.top - 1);
    return e;
}

int In(char c, const char* OP) {
    // 使用 strchr 函数检查 c 是否在 OP 字符串中
    return strchr(OP, c) != NULL;
}

char Precede(char a, char b)
{
    char x[10] = { '+','-','*','/','(',')','#' };
    char OP[10][10] = { {'>','>','<','<','<','>','>'},
                        {'>','>','<','<','<','>','>'},
                        {'>','>','>','>','<','>','>'},
                        {'>','>','>','>','<','>','>'},
                        {'<','<','<','<','<','=',' '},
                        {'>','>','>','>',' ','>','>'},
                        {'<','<','<','<','<',' ','='} };
    for (int i = 0; i < 7; i++)
    {
        if (a == x[i]) 
        {
            a = i;
        }
        if (b == x[i]) 
        {
            b = i;
        }
    }
    return OP[a][b];
}


char Operate(char p, char theta, char q)
{
    if (theta == '+')return p + q;
    else if (theta == '-')return q - p;
    else if (theta == '*')return p * q;
    else if (theta == '/')
    {
        if (p == 0)
        {
            printf("输入不合法！");
            return INF;
        }
        return q / p;
    }
    else return INF;
}

char EvaluateExpression() {
    // 算术表达式求值的算符优先算法。设OPTR和OPND分别为运算符栈和运算数栈，
    // OP 为运算符集合。
    const char* OP = "+-*/()#";
    char x;
    char theta, p, q;
    Stack OPTR, OPND;
    InitStack(&OPTR);
    Push(&OPTR, '#');
    InitStack(&OPND);
    char c = getchar();
    while (c != '#' || GetTop(OPTR) != '#') {
        printf("OPTR:"); for (int i = 0; i < OPTR.top - OPTR.base; i++)printf("%c ", OPTR.base[i]); puts("");
        printf("OPND:"); for (int i = 0; i < OPND.top - OPND.base; i++)printf("%d ", OPND.base[i]); puts("\n");

        if (!In(c, OP)) {  // 不是运算符则进栈OPND
            Push(&OPND, c - '0');
            c = getchar();
        } 
        else {
            switch (Precede(GetTop(OPTR), c))
            {
            case'<': // 栈顶元素优先权低
                Push(&OPTR, c);
                c = getchar();
                break;
            case'=': // 脱括号并接收下一字符
                Pop(&OPTR, &x);
                c = getchar();
                break;
            case'>': // 退栈并将运算结果入栈
                Pop(&OPTR, &theta);
                Pop(&OPND, &p);
                Pop(&OPND, &q);
                Push(&OPND, Operate(p, theta, q));
                break;
            default:
                break;
            }
        }
    }
    char res = GetTop(OPND);
    DestroyStack(&OPTR);
    DestroyStack(&OPND);
    return res;
}

int main() {
    printf("请输入一串表达式，以等号“#”结尾：");
    printf("最终结果为：%d", EvaluateExpression());
    return 0;
}

⭐️ 中缀、前缀、后缀

Order of operation:

Parentheses (){} []

Exponents (right to lett ) ^

Multiplication and division (left to right)

Addition and Subtraction (left to right)

中缀表达式 Infix : 运算符在运算数的中间

<operand><operator><operand>
缺点：关系符号优先级和结合，所以对计算机来说却不好操作，在计算结果时，往往会将中缀表达式转成其它表达式来操作(一般转成后缀表达式)

前缀表达式 - 波兰表达式 Prefix

<operator><operand><operand>

中缀表达式：(a + b) * c - d 转换为前缀表达式（波兰表达式）：- * + a b c d

特点：一个操作数只能和一个操作符进行结合, 连续出现的两个操作数和在它们之前且紧靠它们的运算符构成一个最小表达式

前缀表达式的计算机求值:

从右至左扫描表达式，遇到数字时，将数字压入堆栈，遇到运算符时，弹出栈顶的两个数，用运算符对它们做相应的计算（栈顶元素和次顶元素），并将结果入栈；重复上述过程直到表达式最左端，最后运算得出的值即为表达式的结果

例如：(3+4)×5-6 对应的前缀表达式就是 - × + 3 4 5 6 , 针对前缀表达式求值步骤如下:

从右至左扫描，将6、5、4、3压入堆栈
遇到+运算符，因此弹出3和4（3为栈顶元素，4为次顶元素），计算出3+4的值，得7，再将7入栈
接下来是×运算符，因此弹出7和5，计算出7×5=35，将35入栈
最后是-运算符，计算出35-6的值，即29，由此得出最终结果

后缀表达式 - 逆波兰表达式 Postfix

<operand><operand><operator>
中缀表达式：(a + b) * c - d 转换为后缀表达式（逆波兰表达式）：a b + c * d -
特点：运算符在式中出现的顺序恰为表达式的运算顺序;每个运算符和在它之前出现且紧靠它的两个操作数构成一个最小表达式
后缀表达式的计算机求值：
从左至右扫描表达式，遇到数字时，将数字压入堆栈，遇到运算符时，弹出栈顶的两个数，用运算符对它们做相应的计算（次顶元素和栈顶元素），并将结果入栈；重复上述过程直到表达式最右端，最后运算得出的值即为表达式的结果
例如: (3+4)×5-6 对应的后缀表达式就是 3 4 + 5 × 6 - , 针对后缀表达式求值步骤如下:
从左至右扫描，将3和4压入堆栈；
遇到+运算符，因此弹出4和3（4为栈顶元素，3为次顶元素），计算出3+4的值，得7，再将7入栈；
将5入栈；
接下来是×运算符，因此弹出5和7，计算出7×5=35，将35入栈；
将6入栈；
最后是-运算符，计算出35-6的值，即29，由此得出最终结果

👉 逆波兰计算器简版

计算器说明

输入一个逆波兰表达式(后缀表达式)，使用栈(Stack)，计算其结果

代码思路

计算后缀表达式无需考虑运算符优先级问题

分为两种情况：

遇到数：压入数栈

遇到运算符：从数栈中弹出两个数，进行计算，计算结果压入数栈

处理完表达式就代表计算完成

#define _CRT_SECURE_NO_WARNINGS *1
#include <stdio.h>
#include <stdlib.h>
#include <string.h>

#define MAX_SIZE 100

typedef struct {
    int top;
    int data[MAX_SIZE];
} Stack;

void push(Stack* s, int item) {
    if (s->top == MAX_SIZE - 1) {
        printf("Stack overflow\n");
        exit(1);
    }
    s->data[++s->top] = item;
}

int pop(Stack* s) {
    if (s->top == -1) {
        printf("Stack underflow\n");
        exit(1);
    }
    return s->data[s->top--];
}

int isOperator(char c) {
    return c == '+' || c == '-' || c == '*' || c == '/';
}

int calculate(int num1, int num2, char op) {
    switch (op) {
    case '+':
        return num1 + num2;
    case '-':
        return num1 - num2;
    case '*':
        return num1 * num2;
    case '/':
        return num1 / num2;
    default:
        printf("Invalid operator\n");
        exit(1);
    }
}

/*
	逆波兰计算器 - 整数
*/
int evaluateRPN(char* suffixExpression) {
    Stack stack;
    stack.top = -1;
    // strtok两个参数：要分割的字符串和分隔符，然后返回分割后的标记。
    char* token = strtok(suffixExpression, " ");
    while (token != NULL) {
        if (isOperator(token[0])) {
            // num2 先出栈，所以 num2 是减数或除数
            int num2 = pop(&stack);
            // num1 后出栈，所以 num1 是被减数或被除数
            int num1 = pop(&stack);
            int res = calculate(num1, num2, token[0]);
            push(&stack, res);
        }
        else {
            // 将字符串 token 转换为整数。这函数会忽略字符串前面的空白字符，直到遇到数字或正负号为止，然后将遇到的数字部分转换为整数。
            push(&stack, atoi(token));
        }
        // 在已经使用strtok函数分割过的字符串上继续分割，使用空格作为分隔符。传入NULL作为第一个参数表示继续从上一次的位置开始分割
        token = strtok(NULL, " ");
    }
    return pop(&stack);
}

int main() {
    char suffixExpression[] = "4 5 * 8 - 60 + 8 2 / +";
    int result = evaluateRPN(suffixExpression);
    printf("The result is: %d\n", result);
    return 0;
}

👉 中缀表达式转后缀表达式

初始化两个栈：运算符栈operStack和储存中间结果的栈tempStack；
从左至右扫描中缀表达式；
遇到操作数时，将其压tempStack；
遇到运算符时，比较其与operStack栈顶运算符的优先级：
如果operStack为空，或栈顶运算符为左括号“(”，则直接将此运算符入tempStack栈（分如下两种情况）
operStack 栈顶为空：之前的优先级别高的运算已经处理完成，已经得到了一个结果，将当前运算符直接压入 operStack 栈即可
operStack 栈顶为左括号：当从operStack 出栈，用于运算后，这对括号中的表达式的值也就计算出来了

如果当前运算符优先级比栈顶运算符的高，也将运算符压入tempStack（当前运算符优先级高，先执行运算）
否则，当前运算符优先级 <= 栈顶运算符优先级，将operStack栈顶的运算符弹出并压入tempStack中（operStack 栈顶运算符优先级高，先执行运算），再次转到(4.1)与operStack中新的栈顶运算符相比较（分如下两种情况）；
一直循环，将 tempStack 栈顶元素取出，直到在 operStack 栈中找到比当前运算符优先级高的运算符，让其先执行运算
如果在 tempStack 栈中找不到比当前运算符优先级高的运算符，则会直接将 operStack 栈掏空，然后将当前运算符压入 tempStack 栈中（放在栈底）

遇到括号时：
如果是左括号“(”，则直接压入operStack，等待与其配对的右括号，因为括号中的表达式需要优先运算
如果是右括号“)”，则依次弹出operStack栈顶的运算符，并压入tempStack，直到遇到左括号为止，此时将这一对括号丢弃（此时括号内的运算完成，并将结果压入了tempStack）

重复步骤2至5，直到表达式的最右边
将operStack中剩余的运算符依次弹出并压入tempStack（operStack 栈中剩下的运算都是优先级相同的运算符，按顺序执行即可）
依次弹出tempStack中的元素并输出，结果的逆序即为中缀表达式对应的后缀表达式

例子：1 + (( 2 + 3 )* 4 ) - 5

扫描到的元素储存中间结果的栈tempStack(栈底 -> 栈顶) 运算符栈operStack(栈底 -> 栈顶) 说明
1 1 空数字，直接入栈 - 3
+ 1 + operStack 为空，直接入栈- 4.1.1
( 1 + ( 左括号，直接入栈 - 5.1
( 1 + ( ( 左括号，直接入栈 - 5.1
2 1 2 + ( ( 数字，直接入栈 - 3
+ 1 2 + ( ( + operStack 栈顶为左括号，直接入栈 - 4.1.2
3 1 2 3 + ( ( + 数字，直接入栈 - 3
) 1 2 3 + + ( 右括号，弹出operStack，并压入tempStack，直到出现左括号 - 5.2
* 1 2 3 + operStack 栈顶为左括号，直接入栈 - 4.1.2
4 1 2 3 + 4 + ( * 数字，直接入栈 - 3
) 1 2 3 + 4 * + 右括号，弹出operStack，并压入tempStack，直到出现左括号 - 5.2
- 1 2 3 + 4 * + - - 与 + 同级，operStack弹出+，+压入tempStack，operStack 为空则 - 压入operStack - 4.3
5 1 2 3 + 4 * + 5 - 数字，直接入栈 - 3
到达最右端 1 2 3 + 4 * + 5 - 空将operStack中剩余的运算符依次弹出并压入tempStack - 8
#define _CRT_SECURE_NO_WARNINGS *1
#include <stdio.h>
#include <stdlib.h>
#include <string.h>
#include <ctype.h> // 用于isspace()函数

#define MAX_SIZE 100

int getPriority(char op) {
    switch (op) {
    case '+':
    case '-':
        return 1;
    case '*':
    case '/':
        return 2;
    default:
        return 0;
    }
}

// 检查字符串是否只包含有效的字符
int isValidExpression(const char* expr) {
    while (*expr) {
        if (!isdigit(*expr) && !isspace(*expr) && strchr("+-*/()", *expr) == NULL) {
            return 0; // 非法字符
        }
        expr++;
    }
    return 1; // 表达式有效
}

int infixToPostfix(const char* infix, char* postfix) {
    if (!isValidExpression(infix)) {
        return 0; // 表达式无效
    }

    char stack[MAX_SIZE];
    int top = -1;
    int j = 0;

    for (int i = 0; infix[i] != '\0'; i++) {
        char token = infix[i];
        if (isdigit(token)) {
            postfix[j++] = token;
        }
        else if (token == '(') {
            stack[++top] = token;
        }
        else if (token == ')') {
            while (top > -1 && stack[top] != '(') {
                postfix[j++] = stack[top--];
            }
            if (top == -1) return 0; // 没有匹配的'('
            top--; // 弹出'('
        }
        else {
            while (top > -1 && getPriority(stack[top]) >= getPriority(token)) {
                postfix[j++] = stack[top--];
            }
            if (token == ')') return 0; // ')' 不是运算符
            stack[++top] = token;
        }
    }

    while (top > -1) {
        postfix[j++] = stack[top--];
    }

    postfix[j] = '\0';
    return 1; // 成功转换
}

int main() {
    char infix[] = "1+((2+3)*4)-5";
    char postfix[MAX_SIZE] = { 0 };

    if (infixToPostfix(infix, postfix)) {
        printf("Infix Expression: %s\n", infix);
        printf("Postfix Expression: %s\n", postfix);
    }
    else {
        printf("Invalid expression.\n");
    }

    return 0;
}

扫描到的元素	储存中间结果的栈tempStack(栈底 -> 栈顶)	运算符栈operStack(栈底 -> 栈顶)	说明
1	1	空	数字，直接入栈 - 3
+	1	+	operStack 为空，直接入栈- 4.1.1
(	1	+ (	左括号，直接入栈 - 5.1
(	1	+ ( (	左括号，直接入栈 - 5.1
2	1 2	+ ( (	数字，直接入栈 - 3
+	1 2	+ ( ( +	operStack 栈顶为左括号，直接入栈 - 4.1.2
3	1 2 3	+ ( ( +	数字，直接入栈 - 3
)	1 2 3 +	+ (	右括号，弹出operStack，并压入tempStack，直到出现左括号 - 5.2
*	1 2 3 +		operStack 栈顶为左括号，直接入栈 - 4.1.2
4	1 2 3 + 4	+ ( *	数字，直接入栈 - 3
)	1 2 3 + 4 *	+	右括号，弹出operStack，并压入tempStack，直到出现左括号 - 5.2
-	1 2 3 + 4 * +	-	- 与 + 同级，operStack弹出+，+压入tempStack，operStack 为空则 - 压入operStack - 4.3
5	1 2 3 + 4 * + 5	-	数字，直接入栈 - 3
到达最右端	1 2 3 + 4 * + 5 -	空	将operStack中剩余的运算符依次弹出并压入tempStack - 8

👉 完整的逆波兰计算器

#define _CRT_SECURE_NO_WARNINGS *1
#include <stdio.h>
#include <stdlib.h>
#include <string.h>
#include <ctype.h> // 用于isspace()函数

#define MAX_SIZE 100

typedef struct {
    int top;
    double data[MAX_SIZE];
} Stack;

void push(Stack* s, double item) {
    if (s->top == MAX_SIZE - 1) {
        printf("Stack overflow\n");
        exit(1);
    }
    s->data[++s->top] = item;
}

double pop(Stack* s) {
    if (s->top == -1) {
        printf("Stack underflow\n");
        exit(1);
    }
    return s->data[s->top--];
}

int getPriority(char op) {
    switch (op) {
    case '+':
    case '-':
        return 1;
    case '*':
    case '/':
        return 2;
    default:
        return 0;
    }
}

// 判断字符是否为操作符
int is_operator(char c) {
    return (c == '+' || c == '-' || c == '*' || c == '/' || c == '(' || c == ')');
}

// 检查字符串是否只包含有效的字符
int isValidExpression(const char* expr) {
    while (*expr) {
        if (!isdigit(*expr) && !isspace(*expr) && strchr("+-*/().", *expr) == NULL) {
            return 0; // 非法字符
        }
        expr++;
    }
    return 1; // 表达式有效
}


int infixToPostfix(const char* infix, char* postfix) {
    if (!isValidExpression(infix)) {
        return 0; // 表达式无效
    }

    char stack[MAX_SIZE];
    int top = -1;
    int j = 0;

    for (int i = 0; infix[i] != '\0'; i++) {
        char token = infix[i];
        if (isdigit(token) || (token == '.' && i + 1 < strlen(infix) && isdigit(infix[i + 1]))) {
            // 复制数字到后缀表达式
            while (isdigit(token) || token == '.') {
                postfix[j++] = token;
                i++;
                token = infix[i];
            }
            postfix[j++] = ' '; // 添加空格以分隔数字
            if (is_operator(token) || (i == strlen(infix)))
            {
                i--;
            }
        }
        else if (token == '(') {
            stack[++top] = token;
        }
        else if (token == ')') {
            while (top > -1 && stack[top] != '(') {
                postfix[j++] = stack[top--];
                postfix[j++] = ' ';
            }
            if (top == -1) return 0; // 没有匹配的'('
            top--; // 弹出'('
        }
        else {
            if (isspace(token)) {
                continue;
            }
            while (top > -1 && getPriority(stack[top]) >= getPriority(token)) {
                postfix[j++] = stack[top--];
                postfix[j++] = ' ';
            }
            if (token == ')') return 0; // ')' 不是运算符
            top++;
            stack[top] = token;
        }
    }

    while (top > -1) {
        if (strchr("(",stack[top]))
        {
            return 0;
        }
        postfix[j++] = stack[top--];
        postfix[j++] = ' ';
    }

    postfix[j] = '\0';
    return 1; // 成功转换
}

double calculate(double num1, double num2, char op) {
    switch (op) {
    case '+':
        return num1 + num2;
    case '-':
        return num1 - num2;
    case '*':
        return num1 * num2;
    case '/':
        return num1 / num2;
    default:
        printf("Invalid operator\n");
        exit(1);
    }
}

/*
    逆波兰计算器 
*/
double evaluateRPN(char* suffixExpression) {
    Stack tempStack;
    tempStack.top = -1;
    // strtok两个参数：要分割的字符串和分隔符，然后返回分割后的标记。
    char* token = strtok(suffixExpression, " ");
    char* double_tpken;
    while (token != NULL) {
        if (is_operator(token[0])) {
            // num2 先出栈，所以 num2 是减数或除数
            double num2 = pop(&tempStack);
            // num1 后出栈，所以 num1 是被减数或被除数
            double num1 = pop(&tempStack);
            double res = calculate(num1, num2, token[0]);
            push(&tempStack, res);
        }
        else {
            // 将字符串 token 转换为double。这函数会忽略字符串前面的空白字符，直到遇到数字或正负号为止，然后将遇到的数字部分转换为整数。
            push(&tempStack, strtod(token, &double_tpken));
        }
        // 在已经使用strtok函数分割过的字符串上继续分割，使用空格作为分隔符。传入NULL作为第一个参数表示继续从上一次的位置开始分割
        token = strtok(NULL, " ");
    }
    return pop(&tempStack);
}

int main() {
    char infix[] = "(12.8 + 20) - 3.55 * 4 + 10 / 5.0";
    char postfix[MAX_SIZE] = { 0 };

    if (infixToPostfix(infix, postfix)) {
        printf("Infix Expression: %s\n", infix);
        printf("Postfix Expression: %s\n", postfix);
        double result = evaluateRPN(postfix);
        printf("The result is: %.2f\n", result);
    }
    else {
        printf("Invalid expression.\n");
    }

    return 0;
}

3.2.5 反转一个字符串或者反转一个链表

反转一个字符串

#define _CRT_SECURE_NO_WARNINGS *1
#include <stdio.h>
#include <stdlib.h>
#include <string.h>
#include <stdbool.h>

typedef struct Node {
	int data;
	struct Node* link;
}Node;
struct Node* top = NULL;

void Push(int x) {
	Node* temp = (Node*)malloc(sizeof(Node));
	if (temp)
	{
		temp->data = x;
		temp->link = top;
		top = temp;
	}
}

void Pop() {
	Node* temp;
	if (top == NULL) return;
	temp = top;
	top = top->link;
	free(temp);
}

int Top() {
	if (top == NULL) {
		printf("Error: Stack is empty\n");
		return -1;  // Return an error value or handle error appropriately
	}
	return top->data;
}

bool IsEmpty() {
	if (top == NULL) {
		return true;
	}
	return false;
}

void Reverse(char* C, int n)
{
	int i;
	for (i = 0; i < n; i++)
	{
		Push(C[i]);
	}
	int j;
	for (j = 0; j < n; j++)
	{
		C[j] = Top();
		Pop();
	}
}

int main() {
	char C[51] = "Hello";
	Reverse(C, strlen(C));
	printf("Output = %s", C);
	return 0;
}

反转一个链表到链栈

#define _CRT_SECURE_NO_WARNINGS *1
#include <stdio.h>
#include <stdlib.h>
#include <string.h>
#include <stdbool.h>


typedef struct Node {
	int data;
	struct Node* link;
}Node;
Node* head; // Linked List
Node* top = NULL; // Stack

// Linked List

void Insert(int data, int n) {
	Node* temp1 = (Node*)malloc(sizeof(Node));
	if (temp1 != NULL) {

		temp1->data = data;
		temp1->link = NULL;

		if (n == 1) {
			temp1->link = head;
			head = temp1;
			return;
		}

		Node* temp2 = head;
		int i;
		for (i = 0; i < n - 2; i++) {
			temp2 = temp2->link;
		}
		temp1->link = temp2->link;
		temp2->link = temp1;

	}
}

void Delete(int n) {
	//if (head == NULL) return;
	Node* temp = head;
	if (n == 1) {
		head = temp->link;
		free(temp);
		return;
	}
	int i;
	for (i = 1; i < n - 1; i++) {
		temp = temp->link;
	}
	Node* temp1 = temp->link;
	temp->link = temp1->link;
	free(temp1);
}

//iteration
void Print(Node* headerNode) {
	Node* temp = headerNode;
	printf("List is: ");
	while (temp != NULL)
	{
		printf("%d ", temp->data);
		temp = temp->link;
	}
	printf("\n");
}


// Stack
void Push(int x) {
	Node* temp = (Node*)malloc(sizeof(Node));
	if (temp)
	{
		temp->data = x;
		temp->link = top;
		top = temp;
	}
}

void Pop() {
	Node* temp;
	if (top == NULL) return;
	temp = top;
	top = top->link;
	free(temp);
}

int Top() {
	if (top == NULL) {
		printf("Error: Stack is empty\n");
		return -1;  // Return an error value or handle error appropriately
	}
	return top->data;
}

bool IsEmpty() {
	if (top == NULL) {
		return true;
	}
	return false;
}


// 反转链表到栈
void ReverseToStack() {
	while (head != NULL) {
		Push(head->data);
		Node* temp = head;
		head = head->link;
		free(temp);
	}
}

int main() {
	Insert(2, 1);
	Insert(4, 2);
	Insert(6, 3);
	Insert(5, 4);
	Print(head);
	ReverseToStack();
	Print(top);
	return 0;
}

使用数组实现的栈反转一个链表

#define _CRT_SECURE_NO_WARNINGS *1
#include <stdio.h>
#include <stdlib.h>
#include <string.h>
#include <stdbool.h>


typedef struct Node {
	int data;
	struct Node* link;
}Node;
Node* head; // Linked List

// Stack
#define MAX_SIZE 101
Node* A[MAX_SIZE];
int top = -1;

// Linked List

void Insert(int data, int n) {
	Node* temp1 = (Node*)malloc(sizeof(Node));
	if (temp1 != NULL) {

		temp1->data = data;
		temp1->link = NULL;

		if (n == 1) {
			temp1->link = head;
			head = temp1;
			return;
		}

		Node* temp2 = head;
		int i;
		for (i = 0; i < n - 2; i++) {
			temp2 = temp2->link;
		}
		temp1->link = temp2->link;
		temp2->link = temp1;

	}
}

void Delete(int n) {
	//if (head == NULL) return;
	Node* temp = head;
	if (n == 1) {
		head = temp->link;
		free(temp);
		return;
	}
	int i;
	for (i = 1; i < n - 1; i++) {
		temp = temp->link;
	}
	Node* temp1 = temp->link;
	temp->link = temp1->link;
	free(temp1);
}

//iteration
void Print() {
	Node* temp = head;
	printf("List is: ");
	while (temp != NULL)
	{
		printf("%d ", temp->data);
		temp = temp->link;
	}
	printf("\n");
}


// Stack
void Push(Node* x)
{
	if (top == MAX_SIZE - 1)
	{
		printf("Error:stack overflow\n");
		return;
	}
	A[++top] = x;
}

void Pop() {
	if (top == -1) {
		printf("Error: No element to pop\n");
		return;
	}
	top--;
}

Node* Top()
{
	if (top != -1)
	{
		return A[top];
	}
	return;
}

void Reverse()
{
	if (head == NULL)
	{
		return;
	}
	Node* temp = head;
	while (temp != NULL)
	{
		Push(temp);
		temp = temp->link;
	}
	Node* temp1 = Top();
	head = temp1;
	Pop();
	while (top != -1)
	{
		temp1->link = Top();
		Pop();
		temp1 = temp1->link;
	}
	temp1->link = NULL;
}

int main() {
	Insert(1, 1);
	Insert(4, 2);
	Insert(6, 1);
	Insert(3, 3);
	Print();
	Reverse();
	Print();
	return 0;
}

3.3 栈与递归的实现

多个函数嵌套调用的规则是：后调用先返回此时的内存管理实行““栈式管理”

一个递归函数的运行过程类似于多个函数的嵌套调用,只是调用函数和被调用函数是同一个函数。

当在一个函数的运行期间调用另一个函数时，在运行该被调用函数之前，需先完成三件事:

将所有的实在参数、返回地址等信息传递给被调用函数保存；
为被调用函数的局部变量分配存储区；
将控制转移到被调用函数的入口。

从被调用函数返回调用函数之前，应该完成:

保存被调函数的计算结果；
释放被调函数的数据区；
依照被调函数保存的返回地址将控制转移到调用函数。

函数之间的信息传递和控制转移必须通过“栈”来实现,即系统将整个程序运行时所需的数据空间安排在一个栈中,每当调用一个函数时,就为它在栈顶分配一个存储区,每当从一个函数退出时,就释放它的存储区,则当前正运行的函数的数据区必在栈顶。

递归过程指向过程中占用的数据区，称之为递归工作栈
每一层的递归参数合成一个记录，称之为递归工作记录
栈顶记录指示当前层的执行情况，称之为当前活动记录
栈顶指针，称之为当前环境指针

汉诺塔:

汉诺塔问题的描述如下：有三根柱子，A、B、C。A柱子上从下往上按大小顺序叠放着n个圆盘，目标是将这n个圆盘移动到C柱子上。移动过程中必须遵守以下规则：

一次只能移动一个圆盘。
大圆盘不能叠放在小圆盘上。
可以利用B柱子作为辅助柱子。

对于任何一个具体的步骤，实际上都需要进行3次移动：

将上面的 n-1 个盘子从起始柱子（如 A）移到另一个柱子（如 B）；
将最大的盘子从起始柱子移到目标柱子（如 C）；
最后，将 n-1 个盘子从临时柱子（如 B）移到目标柱子（如 C）。

#define _CRT_SECURE_NO_WARNINGS *1
#include <stdio.h>

// 将n个盘子从start移动到end，通过temporary辅助
void towerOfHanoi(int n, char start, char end, char temporary) {
    if (n == 1) {
        printf("Move disk 1 from %c to %c\n", start, end);
        return;
    }

    // 首先将n-1个盘子从start移动到temporary
    towerOfHanoi(n - 1, start, temporary, end);

    // 然后将最大的盘子从start移动到end
    printf("Move disk %d from %c to %c\n", n, start, end);

    // 最后将n-1个盘子从temporary移动到end
    towerOfHanoi(n - 1, temporary, end, start);
}

int main() {
    int n; // 盘子的数量
    printf("Enter the number of disks: ");
    scanf("%d", &n);

    // 开始移动盘子，'A'是起始位置，'B'是辅助位置，'C'是目标位置
    towerOfHanoi(n, 'A', 'C', 'B');
    return 0;
}

3.4 队列 - Queue

3.4.1 抽象数据类型队列的定义

队列(queue)是一种先进先出(first in first out, FIFO)的线性表。它只允许在表的一端进行插入,而在另一端删除元素。

在队列中，允许插人的一端叫做队尾(rear)，允许删除的一端则称为队头(front)。

在这里插入图片描述

队列的抽象数据类型的定义：

在这里插入图片描述

3.4.2 链队列–队列的链式表示和实现

在这里插入图片描述

#define _CRT_SECURE_NO_WARNINGS *1
#include <stdio.h>
#include <stdlib.h>

#define MAXQSIZE 10
#define OK 1
#define OVERFLOW -1
#define ERROR -2

typedef struct Node {
    int data;
    struct Node* next;
}Node;
Node* front = NULL;
Node* rear = NULL;

void Enqueue(int x) {
    Node* temp = (Node*)malloc(sizeof(Node));
    if (!temp) {
        exit(1); // 内存分配失败，退出程序
    }
    temp->data = x;
    temp->next = NULL;
    if (front == NULL && rear == NULL) {
        front = rear = temp;
        return;
    }
    rear->next = temp;
    rear = temp;
}

void Dequeue() {
    Node* temp = front;
    if (front == NULL) return;
    if (front == rear) {
        front = rear = NULL;
    }
    else
    {
        front = front->next;
    }
    printf("Dequeue : %d\n", temp->data);
    free(temp);
}

int main() {
    Enqueue(1);
    Enqueue(2);
    Enqueue(3);
    Dequeue();
    Dequeue();
    Dequeue();
    return 0;
}

3.4.3 循环队列–队列的顺序表示和实现

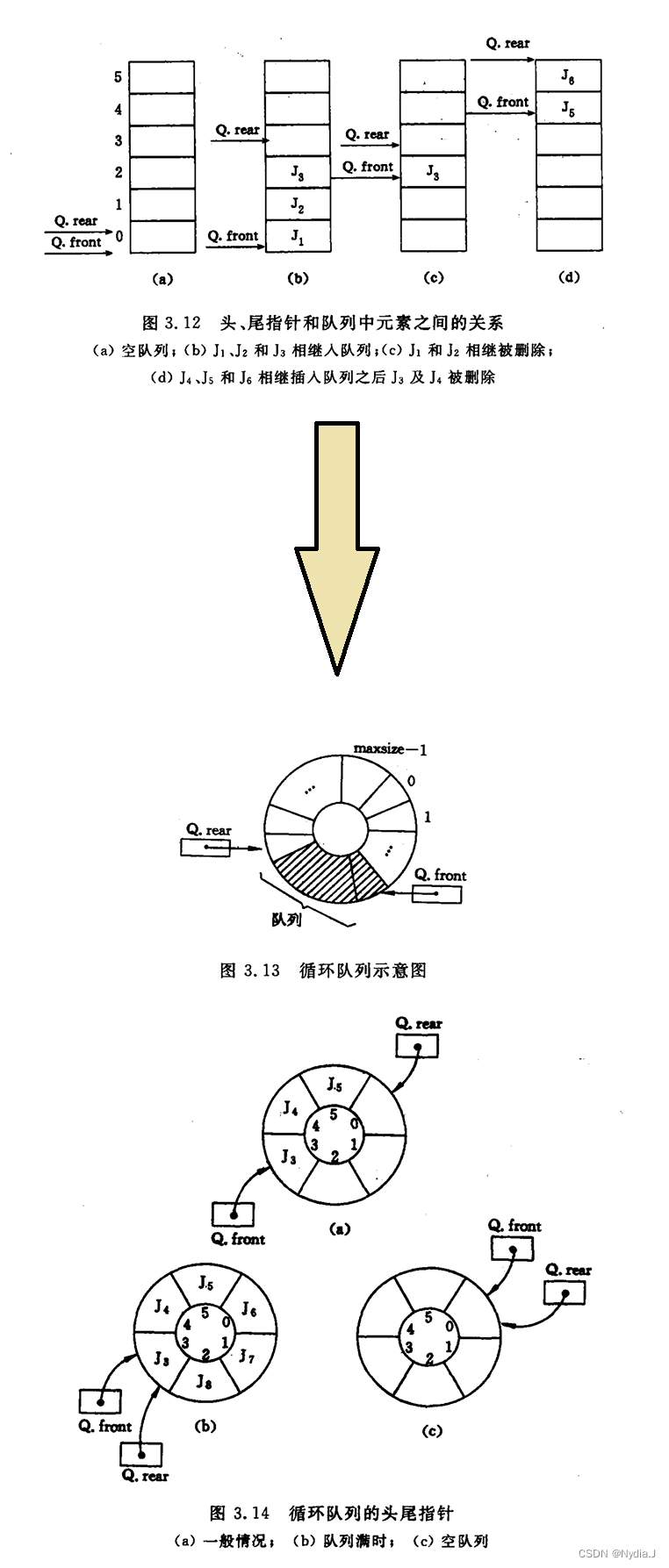
在这里插入图片描述

#define _CRT_SECURE_NO_WARNINGS *1
#include <stdio.h>
#include <stdlib.h>

#define MAXQSIZE 10
#define OK 1
#define OVERFLOW -1
#define ERROR -2

typedef int Status;
typedef struct {
    int* base;
    int front;
    int rear;
} SqQueue;

Status InitQueue(SqQueue* Q) {
    Q->base = (int*)malloc(MAXQSIZE * sizeof(int));
    if (!Q->base) exit(1); // 使用exit(1)表示错误退出
    Q->front = Q->rear = 0;
    return OK;
}

Status EnQueue(SqQueue* Q, int e) {
    if ((Q->rear + 1) % MAXQSIZE == Q->front) {
        return OVERFLOW; // 队列已满，返回OVERFLOW
    }
    Q->base[Q->rear] = e;
    Q->rear = (Q->rear + 1) % MAXQSIZE;
    return OK;
}

Status DeQueue(SqQueue* Q, int* e) {
    if (Q->front == Q->rear) {
        return ERROR; // 队列为空，返回ERROR
    }
    *e = Q->base[Q->front]; // 使用引用来修改e的值
    Q->front = (Q->front + 1) % MAXQSIZE;
    return OK;
}

void DestroyQueue(SqQueue* Q) {
    free(Q->base);
    Q->base = NULL;
    Q->front = Q->rear = 0;
}

int main() {
    SqQueue Q;
    if (InitQueue(&Q) == OK) {
        EnQueue(&Q, 1);
        EnQueue(&Q, 2);
        EnQueue(&Q, 3);
        int e;
        if (DeQueue(&Q, &e) == OK) {
            printf("%d ", e);
        }
        if (DeQueue(&Q, &e) == OK) {
            printf("%d ", e);
        }
        if (DeQueue(&Q, &e) == OK) {
            printf("%d", e);
        }
    }
    DestroyQueue(&Q);
    return 0;
}