目录
1. 原理介绍
2. 代码实现
1. 原理介绍
梯度下降法(Gradient Descent)是一种用于优化函数的迭代算法,广泛应用于机器学习和深度学习中,用来最小化一个目标函数。该目标函数通常代表模型误差或损失。
基本思想是从一个初始点出发,通过不断沿着目标函数的负梯度方向更新参数,逐步逼近函数的局部最小值(或者全局最小值)。梯度是目标函数相对于参数的导数,因此,负梯度方向是函数值下降最快的方向。
具体步骤如下:
1. **初始化参数**:随机选择模型初始参数 \( \theta_0 \)。
2. **计算梯度**:计算目标函数关于当前参数的梯度 \( \nabla J(\theta) \),这里 \( J(\theta) \) 是目标函数。
3. **更新参数**:根据梯度和学习率 \( \alpha \) 更新参数:
\[
\theta := \theta - \alpha \nabla J(\theta)
\]
其中,学习率 \( \alpha \) 是一个预先设置的超参数,决定了每一步更新的大小。
4. **重复**:重复步骤 2 和 3 直到收敛,即参数不再发生显著变化或者达到预设的迭代次数。
- 变种
梯度下降法有几种常见变种:
1. **批量梯度下降(Batch Gradient Descent)**:每一步更新使用整个训练数据集计算梯度。这对于大规模数据集可能会非常耗时。
2. **随机梯度下降(Stochastic Gradient Descent, SGD)**:每一步更新使用单个样本计算梯度,通过不断地用单个样本更新,效率较高但引入了较大的波动。
3. **小批量梯度下降(Mini-batch Gradient Descent)**:每一步更新使用一个小批量的样本来计算梯度,结合了批量梯度下降和随机梯度下降的优点。
- 优化
为了提高梯度下降的效率和效果,可以结合一些优化方法,如:
- **动量法**:在每一步更新中添加动量,帮助跳出局部最小值。
- **AdaGrad**、**RMSprop**、**Adam**:这些算法通过自适应调整学习率,以适应不同参数和不同迭代阶段。
梯度下降法是机器学习和深度学习中的关键技术之一,通过梯度下降可以有效地训练模型并优化目标函数。
2. 代码实现
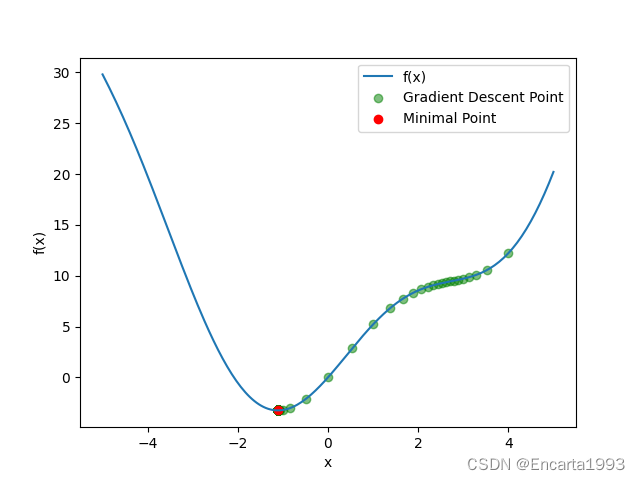
以下用梯度下降法求解函数的最小值:
import numpy as np
import matplotlib.pyplot as plt
def f(x):
return x ** 2 + 5 * np.sin(x)
def df(x):
return 2 * x + 5 * np.cos(x)
# initialize parameter and learning rate
x = 4
lr = 0.1
epochs = 1000
history = [x]
for _ in range(epochs):
x = x - lr * df(x)
history.append(x)
xs = np.linspace(-5, 5, 200)
ys = f(xs)
plt.plot(xs, ys, label="f(x)")
plt.xlabel("x")
plt.ylabel("f(x)")
plt.scatter(history, f(np.array(history)), c="g", alpha=0.5, label="Gradient Descent Point")
plt.scatter(history[-1], f(history[-1]), c="r", label="Minimal Point")
plt.legend()
plt.show()