选择排序和快排
- 选择排序
- 时间复杂度和空间复杂度
- 快排(三种方式)
- 1.hoar
- 时间复杂度和空间复杂度
- 优化--三数取中
- 优化--小区间优化
- 2.挖坑法
- 3.双指针(推荐)
选择排序
本篇文章的重点在快排。因为选择排序无论是在思想上面还是,代码上面,都是比较容易理解的,所以,就不说的那么详细了。
选择排序的思想(默认的实现升序)
每一次遍历数组,选取最大的(或者是最小的)与数组的最后一个数据(或者第一个数据)进行交换。
在上面的思想上进行一定的优化
优化:每一次遍历数组时,同时选取最大的和最小的,分别与数组的最后一个数据和第一个数据进行交换。
下面实现的是优化的方案(第一种太简单了,而且没什么坑,因此不写了)
#include <stdio.h>
void Swap(int* x, int* y)
{
int tmp = *x;
*x = *y;
*y = tmp;
}
void Select(int* a, int n)
{
int left = 0;
int right = n-1;
while(left < right)
{
//先默认选取数组中的第一个数据作为最大值和最小值
int max = left;
int min = left;
int i = 0;
//遍历数组选取本次遍历的最大值和最小值
for(i = left+1; i <= right; ++i)
{
if(a[i] > a[max])
max = i;
if(a[i] < a[min])
min = i;
}
//让最小值排在前面
Swap(&a[left], &a[min]);
if(max == left)
max = min;
//最大值排在后面
Swap(&a[right], &a[max]);
left++;
right--;
}
}
void Test()
{
int arr[] = {3,2,1,-1,4,5,6,10,9,8,7};
int sz = sizeof(arr) / sizeof(arr[0]);
Select(arr, sz);
int i;
for(i = 0; i < sz; ++i)
{
printf("%d ", arr[i]);
}
printf("\n");
}
int main()
{
Test();
return 0;
}
对于代码中,在交换完 Swap(&a[left], &a[min]); 后
为什么会增加一个if()判断,下面来解释一下。
假设我们的数组起始数据为arr[] = {6,4,3,1,2,0,3};
那么在第一次选取最大和最小值的时候,max = 0 , min = 5;
在进行完Swap(&a[left], &a[min])之后,max原本是指向最大值6的位置0,但是此刻的位置0上的数字已经变成了最小值0,而6来到了min的位置,所以当max的位置和left重复时,我们执行max = min 让max重新指向最大的值。
时间复杂度和空间复杂度
选择排序每一次都需要遍历一次数组来确定最大值或最小值,一共需要遍历n次
所以时间复杂度为O(n^2)
空间复杂度为O(1)
快排(三种方式)
快排在最早的时候是由霍尔提出的。
霍尔 (Sir Charles Antony Richard Hoare) 是一位英国计算机科学家,他是著名的快速排序 (QuickSort) 的发明者。在平均状况下,**排序 n 个项目要Ο(n log n) 次比较,而且通常明显比其他Ο(n log n) 演算法更快。**所以它是一个被广泛使用的算法。在一次采访中。
在一开始的时候,快排的实现方式只有一种,就是霍尔大佬提出的思路,后面还有两种挖坑发和双指针法,可以是说对第一种思路的优化吧,所以第一种的实现思路也是这三种方法中最复杂的一个。
1.hoar
废话不多说,下面我们直接先给出思路的文字解释,然后再结合画图的方式,帮助大家更好的理解快排的基本实现思路。
hora思路解释(文字)
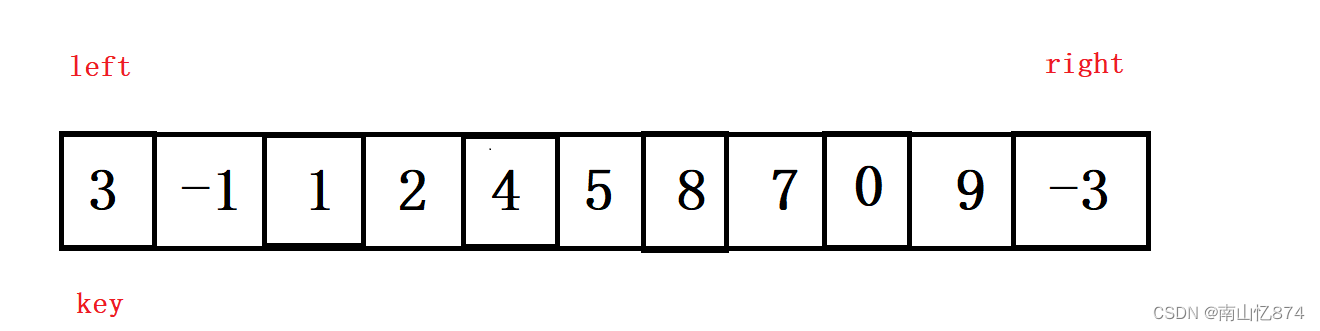
我们假设以数组arr[] = {3,-1,1,2,4,5,8,7,6,9,-3}为例(以排升序为例)。
要理解快排的基本思路,要有一个前提,知道key,left,right。
首先要先选取一个数作为key,这个数字通常一开始是数组中的第一个数字,也就是3。
然后再定义两个指针,left和right,如下图:
接下来我们就开始正式去按照规则走一遍:
1.right要先走,找比key要小的(不包含等于key),-3就比3小,所以right就不用动。
2.left再走,找比key要大的,那么不断的加加到4的位置,如下图:
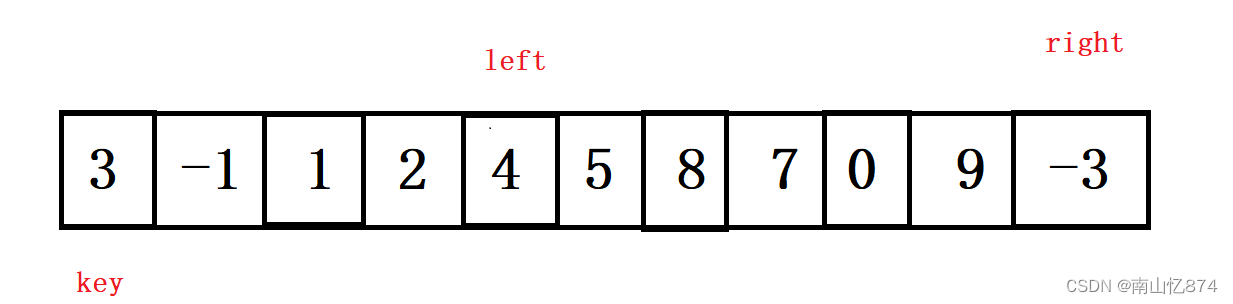
等right和left都找到了对应的位置,那么交换left和right。即下图:
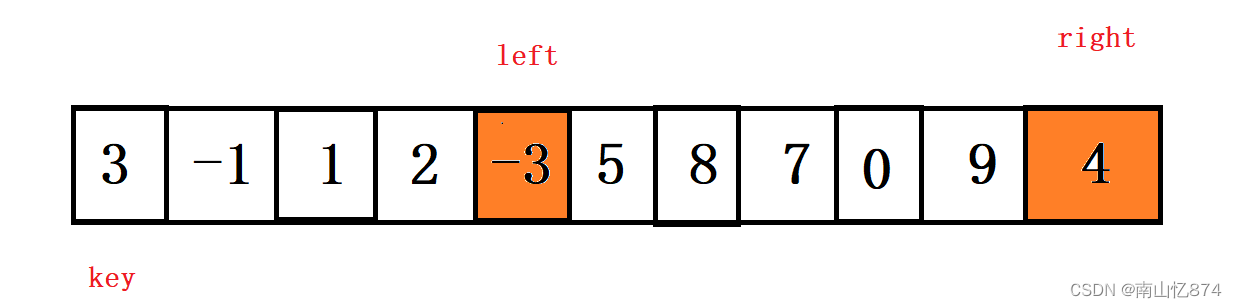
然后还是right先走,还是找比key小的,然后left再走,找比key大的。如下图:
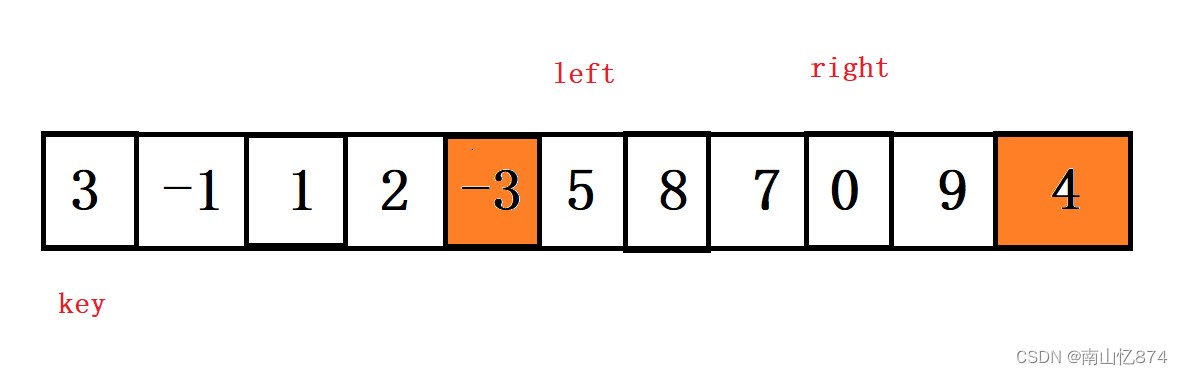
然后再交换left和right,即下图:
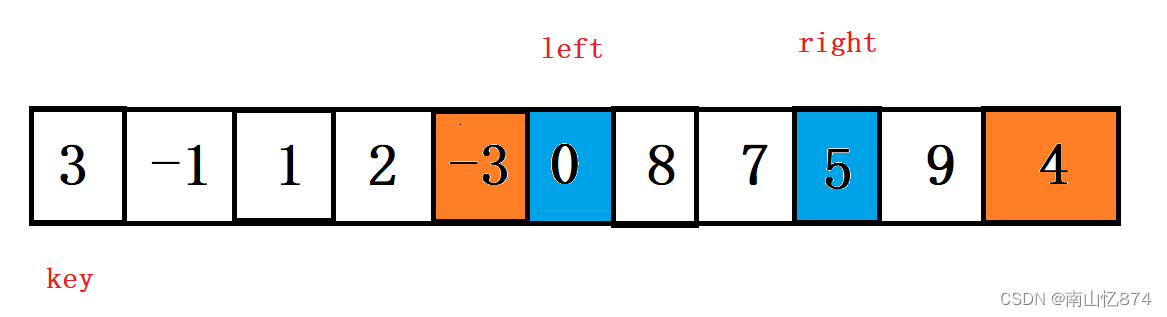
然后还是right先走,找比key小的
但是注意当right <= left时,本次查找就结束。
然后再交换left和key。
如下图:
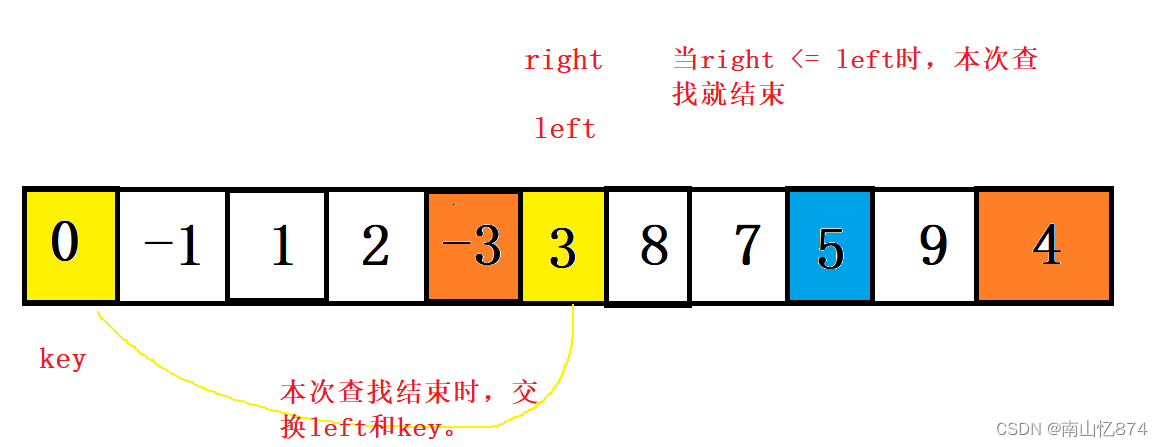
这称为一次查找结束,当一次查找结束后,我们可以发现几点
- key来到了正确的位置
- key的左边都是比key小的值
- 右边都是比key大的值
此时,精华来了!!
我们可以以key为中点,划分三个区间,如下图:
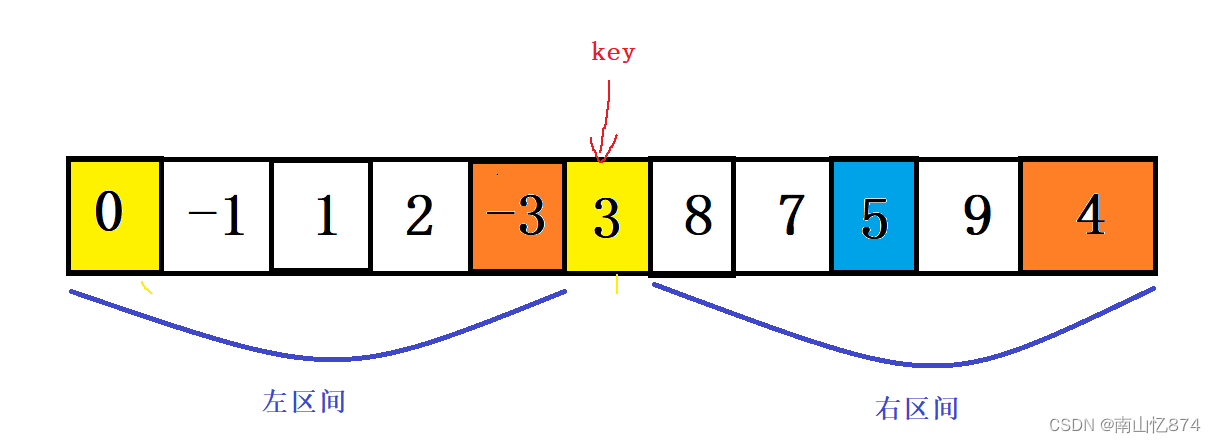
我们再把左区间和右区间按照上述的步骤再去走,直到全部有序了,就结束,可以把这个过程看作成一个二叉树的前序遍历!
图解:
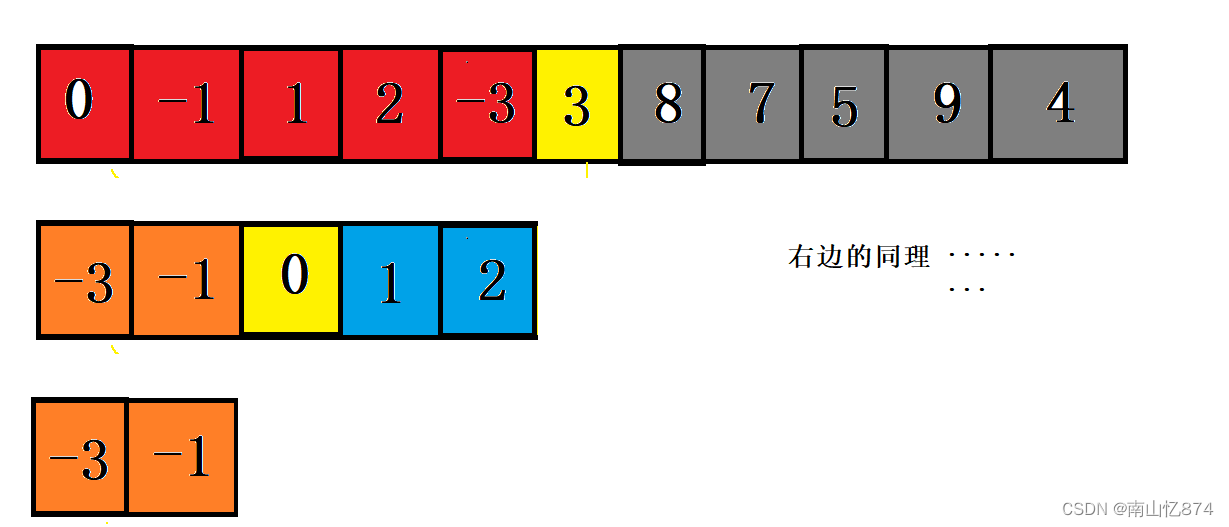
不难看出这是一个递归调用的过程,递归结束的条件就是非法区间。
代码:
void Swap(int* x, int* y)
{
int tmp = *x;
*x = *y;
*y = tmp;
}
void quick(int* a, int begin, int end)
{
//递归的结束条件
if(begin >= end)
return;
//选key
int key = begin;
int left = begin;
int right = end;
while(left < right)
{
//右边先走,找比key小的
while(right > left && a[right] >= a[key])
{
right--;
}
//左边的再走,找比key大的
while(right > left && a[left] <= a[key])
{
left++;
}
//大的数据向后走,小的向前来
Swap(&a[left], &a[right]);
}
//使得key来到了正确的位置,并且以key划分了区间[left, key-1] key [key+1, end]
Swap(&a[key], &a[left]);
//递归--前序遍历
quick(a, begin, key-1);
quick(a, key+1, end);
}
void Test()
{
int arr[] = {3,-1,1,2,4,5,8,7,6,9,-3};
int sz = sizeof(arr) / sizeof(arr[0]);
quick(arr, 0, sz-1);
int i = 0;
for(; i < sz; ++i)
{
printf("%d ", arr[i]);
}
printf("\n");
}
int main()
{
Test();
return 0;
}
值得一提的是,在left和right寻找对应的值的时候,我们需要添加一个结束的条件即left < right。
假设我们的数据是3,4,7,8,9,6,6,10.
我们的left < right就是防止这种极端的数据出现(没有比key大的或没有比key小的),防止我们在访问数组时,出现数组越界的问题。
时间复杂度和空间复杂度
在一开始我们就提出了快排的时间复杂度是O(NlogN),为什么是O(n)我想大家能理解,每一次查找都是需要,遍历完区间的。
至于问什么有logn,是递归调用。这一点,大家学过堆排的话应该都知道,如果不清楚的话可以看一下我写的堆排的文章,里面有分析关于这块的时间复杂度。
https://blog.csdn.net/Javaxaiobai/article/details/128016533?spm=1001.2014.3001.5502
优化–三数取中
首先声明一下,上述就是快排完整的第一种实现思路和方式,下面的三数取中和小区间优化,是人们在使用时,对特殊数据的优化处理,特别是三数取中。
三数取中就是解决顺序或逆序的极端情况(递归调用的太多,可能会导致Stack Overflow)。
假设我们在处理的数据是有序的。(1,2,3,4,5,6,7,8,9,10…)
那么这就会导致left并不会移动,每一次划分的区间实际上是无效的(即交换left和key没有实际达到划分区间的目的),那么在递归调用的时候,就是造成了下图的情况。
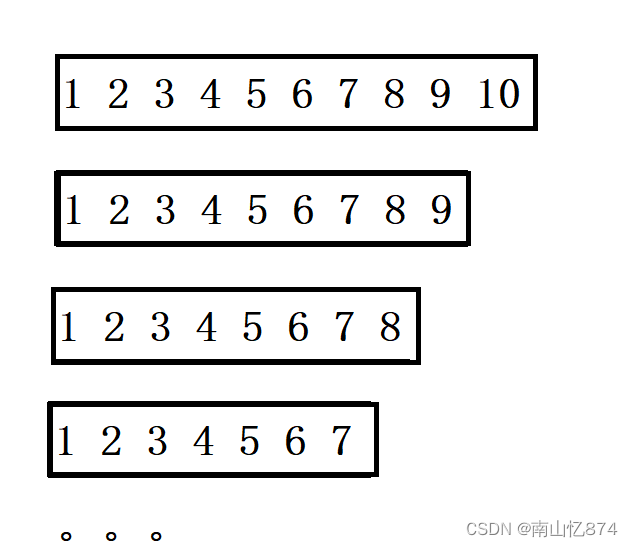
递归的时间复杂度就是O(n)不再是O(logn)。
那么整体的时间复杂度就是O(n^2)!!!!
三数取中说白了就是,在三个数中,选取中间值。三个数分别对应了数组的第一个数,数组的中间值,数组的最后一个数字。之后再将第一个数字和选取的中间值进行交换。
三数取中的逻辑并不难理解,直接给出代码,就是在三个数中选取中间值。
int GetMin(int* a, int begin, int end)
{
int min = (begin + end) / 2;
if (a[begin] < a[min])
{
if (a[min] < a[end])
{
return min;
}
else if(a[begin] > a[end])
{
return begin;
}
else
{
return end;
}
}
else //a[begin] > a[min]
{
if (a[min] > a[end])
{
return min;
}
else if (a[end] > a[begin])
{
return begin;
}
else
{
return end;
}
}
}
优化–小区间优化
小区间优化–最后的小区间不再继续的递归下去,而是使用插入排序进行(优化空间 %75左右)。
因为递归调用是需要在内存中进行压栈的,当时数据量不太大的时候就没必要使用递归了,直接使用快排,对剩下的数据做排序。
以下就是添加了三数取中和小区间优化的最终代码
int GetMin(int* a, int begin, int end)
{
int min = (begin + end) / 2;
if (a[begin] < a[min])
{
if (a[min] < a[end])
{
return min;
}
else if(a[begin] > a[end])
{
return begin;
}
else
{
return end;
}
}
else //a[begin] > a[min]
{
if (a[min] > a[end])
{
return min;
}
else if (a[end] > a[begin])
{
return begin;
}
else
{
return end;
}
}
}
void Swap(int* x, int* y)
{
int tmp = *x;
*x = *y;
*y = tmp;
}
void quick(int* a, int begin, int end)
{
//递归的结束条件
if(begin >= end)
return;
int min = GetMin(a, begin, end);
Swap(&a[min], &a[begin]);
int key = begin;
int left = begin;
int right = end;
if (end - begin + 1 < 15)
{
InsertSort(a + begin, end - begin + 1);//闭区间+1才是数据的个数
}
else
{
while(left < right)
{
//右边先走,找比key小的
while(right > left && a[right] >= a[key])
{
right--;
}
//左边的再走,找比key大的
while(right > left && a[left] <= a[key])
{
left++;
}
//大的数据向后走,小的向前来
Swap(&a[left], &a[right]);
}
//使得key来到了正确的位置,并且以key划分了区间[left, key-1] key [key+1, end]
Swap(&a[key], &a[left]);
//递归--前序遍历
quick(a, begin, key-1);
quick(a, key+1, end);
}
}
void Test()
{
int arr[] = {3,-1,1,2,4,5,8,7,6,9,-3};
int sz = sizeof(arr) / sizeof(arr[0]);
quick(arr, 0, sz-1);
int i = 0;
for(; i < sz; ++i)
{
printf("%d ", arr[i]);
}
printf("\n");
}
int main()
{
Test();
return 0;
}
接下来我们介绍第二种方法–挖坑法
2.挖坑法
挖坑法其实本质上和第一种实现的思路和方式都一样,只不过需要新增一个变量hole。
实现思路
我们还是以上一组数据arr[] = {3,-1,1,2,4,5,8,7,6,9,-3}为例。
前提仍然是需要先选取key和left和right,如下图:
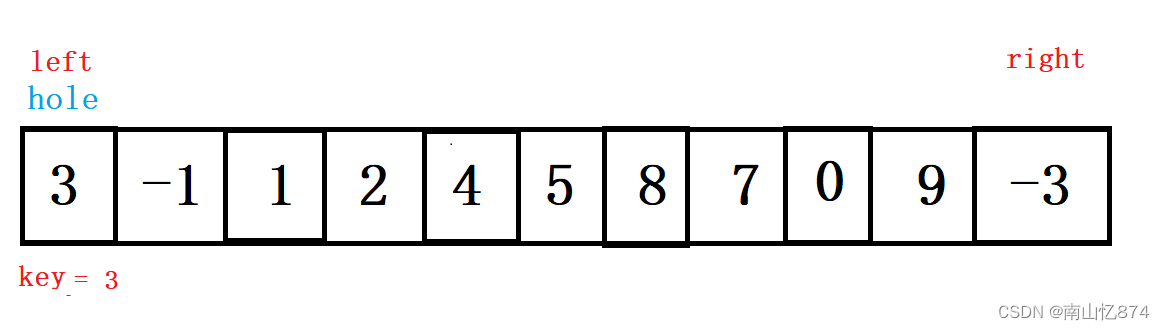
不过我们需要在left的位置新增一个hole变量,它的作用就是取代了,交换left和right。不理解没关系,下面跟着走一遍就能清楚了。
另外一点是,key不再是记录的是位置,而是值!!
还是老规矩,让我们的right先走,找比key要小的。
再之后将right位置上的值赋值给hole位置上去,因为我们使用key记录下的是该位置的值,所以不用害怕改值丢失。
赋值完成后,再将hole移动到right的位置,为下一次left的值做填充准备!
如下图:
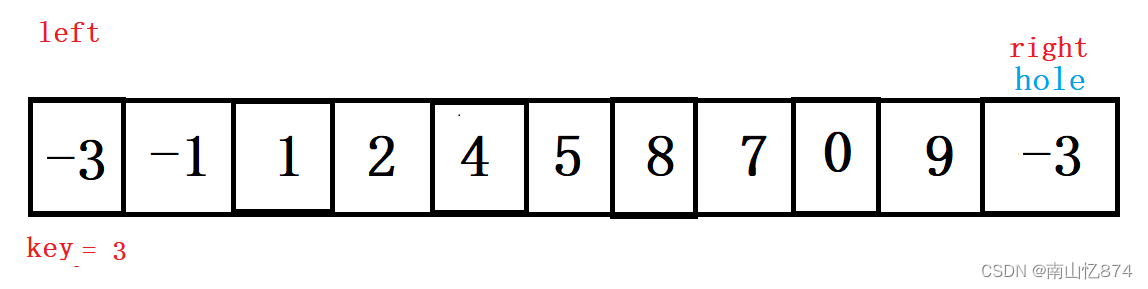
然后就轮到我们的left再走了,依然是找比key大的值,找到了之后将该值填入到hole的位置上去。
如下图所示:
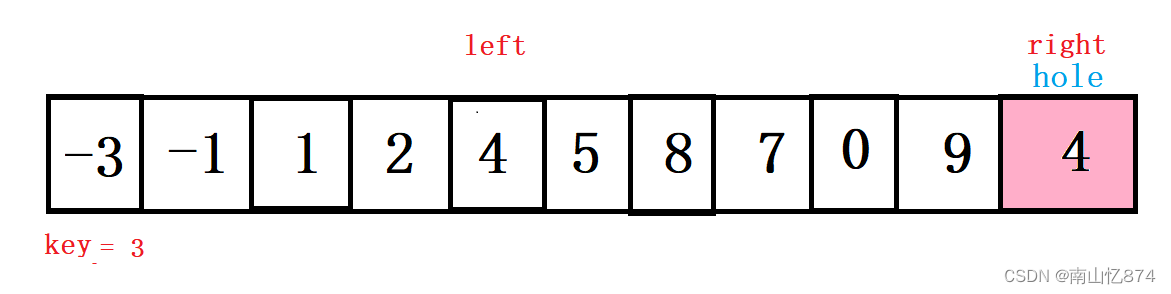
然后还是再移动hole的位置到left:为下一次right的值做填充准备!
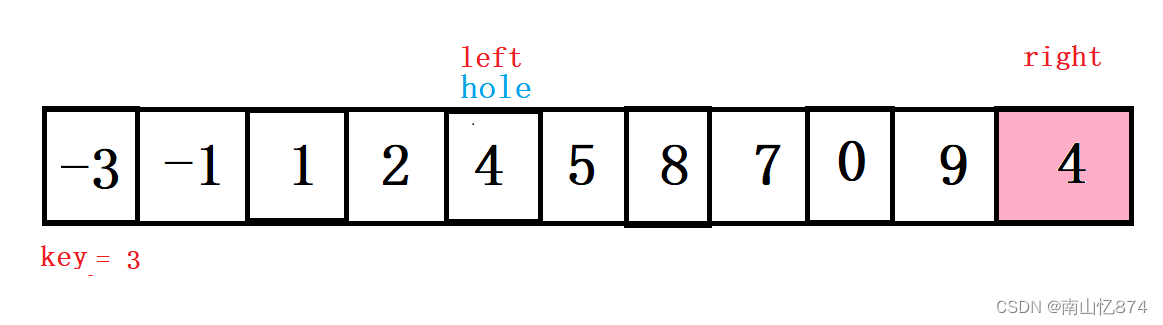
中间重复的过程我就不再继续的画下去了,我们来看最后结尾处:
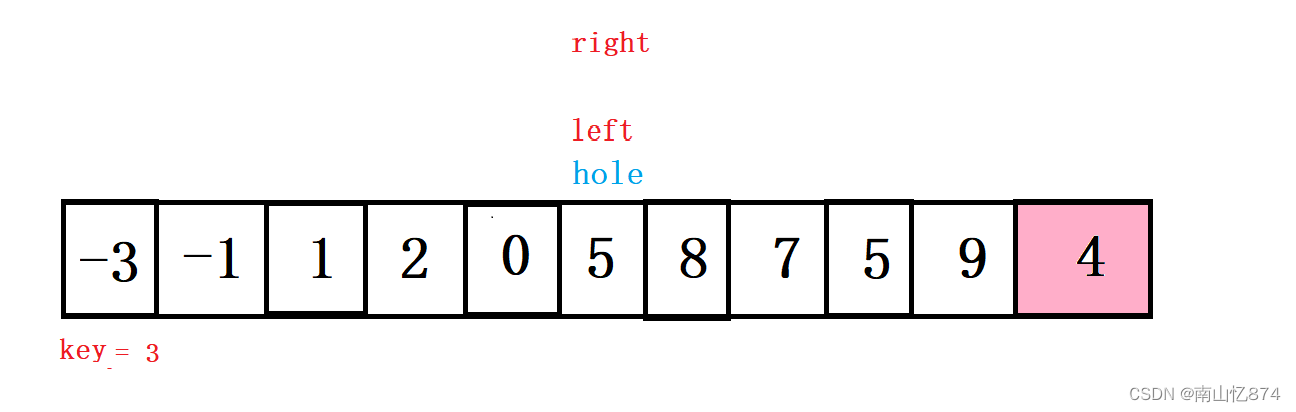
此时left和right相遇了,再将hole移动到left的位置,循环结束,接下来要做的最后一步就是将key赋值给hole位置上!
如下图:
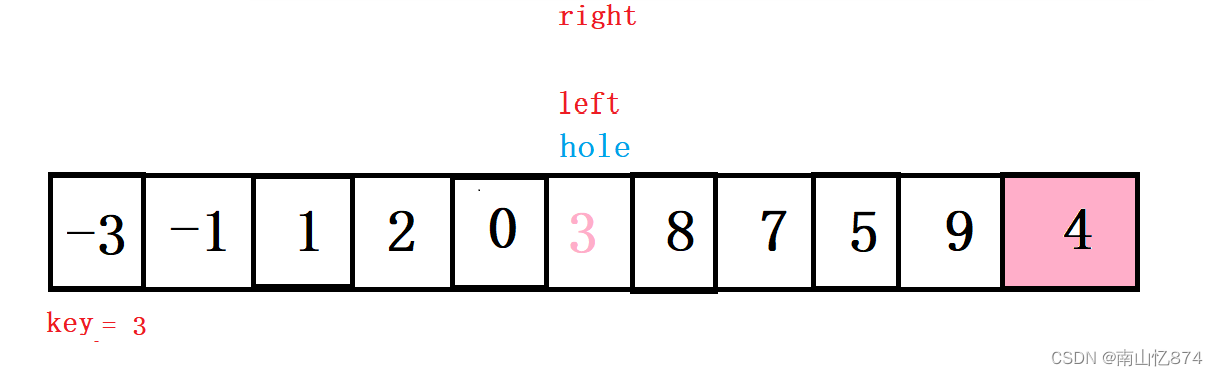
此时我们发现,hole左边的全是比hole小的值,右边的全部是比key大的值。
接下来的过程就和第一次的不步骤一样了,划分区间和递归的去走下去。递归结束的条件还是一样的。
代码:
void quick1(int*a , int begin, int end)
{
if(begin >= end) return;
//挖坑法
int left = begin, right = end;
int key = a[left];
int hole = left;
while(left < right)
{
//还是right先走,找比key小的
while(left < right && a[right] >= key)
{
right--;
}
a[hole] = a[right];
hole = right;
//left再走,找比key大的
while(left < right && a[left] <= key)
{
left++;
}
a[hole] = a[left];
hole = left;
}
a[hole] = key;
quick1(a, begin, hole-1);
quick1(a, hole+1, end);
}
关于三数取中和小区间优化也是和上面的一样,我在代码上面就不再重复的展示了。
3.双指针(推荐)
下面就是最后一种—双指针法。
双指针的代码较少,但是非常的精华,也是我个人比较喜欢的一种方式。
还是以上面的数据arr[] = {3,-1,1,2,4,5,8,7,6,9,-3}为例
前提还是要给给大家说一下的,我们定义两个指针,prev和cur,开始的时候,两个指针都是指向第一个数据的
,同样我们还是选取第一个数据作为我们的key。
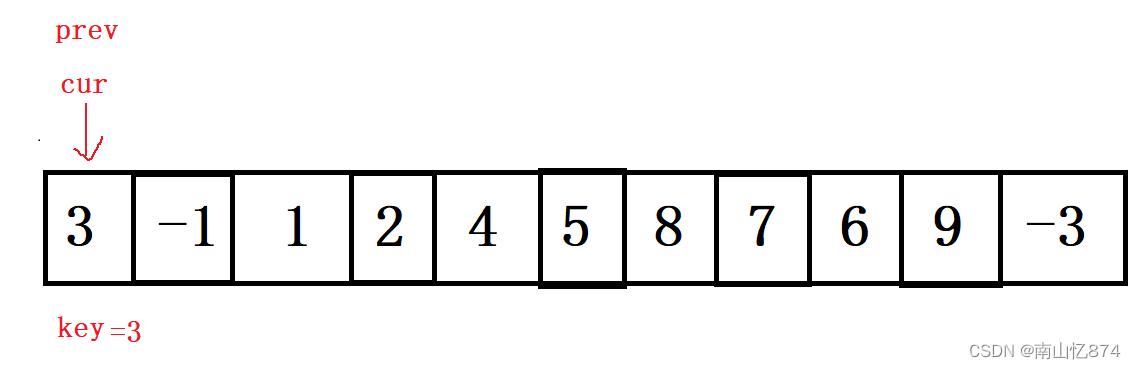
接下来我们再来谈思路(升序)
首先cur指针先走一步,找比key小的数字
- 如果找到了,先再让prev走一步,此时如果prev和cur的位置不重复,就交换cur和prev的数据,否则cur 继续向前走一步,prev不动。
- 如果没找到,cur继续向前走,prev不动。
根据上面给出的数据,按照以上的规则进行走,过程如下:
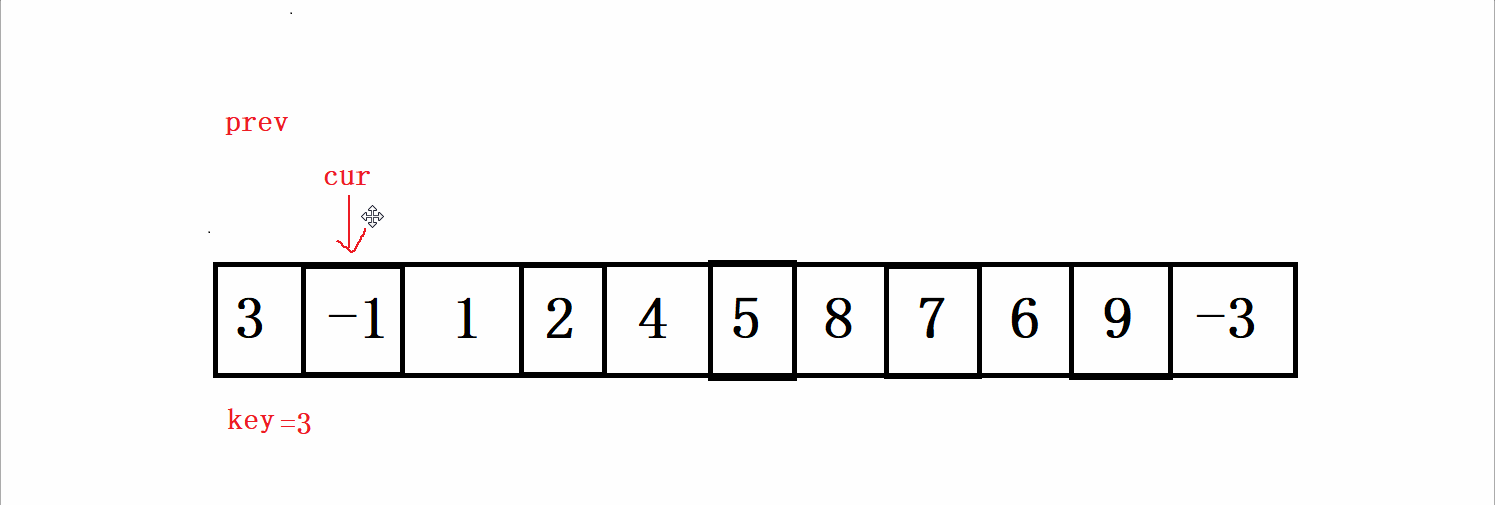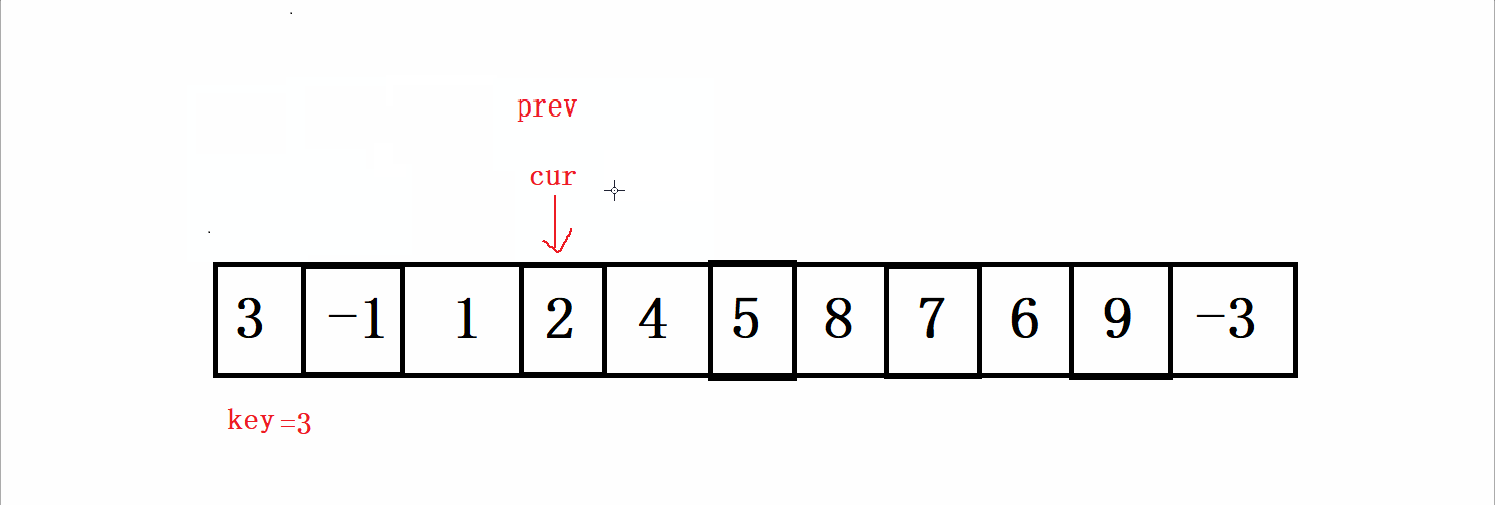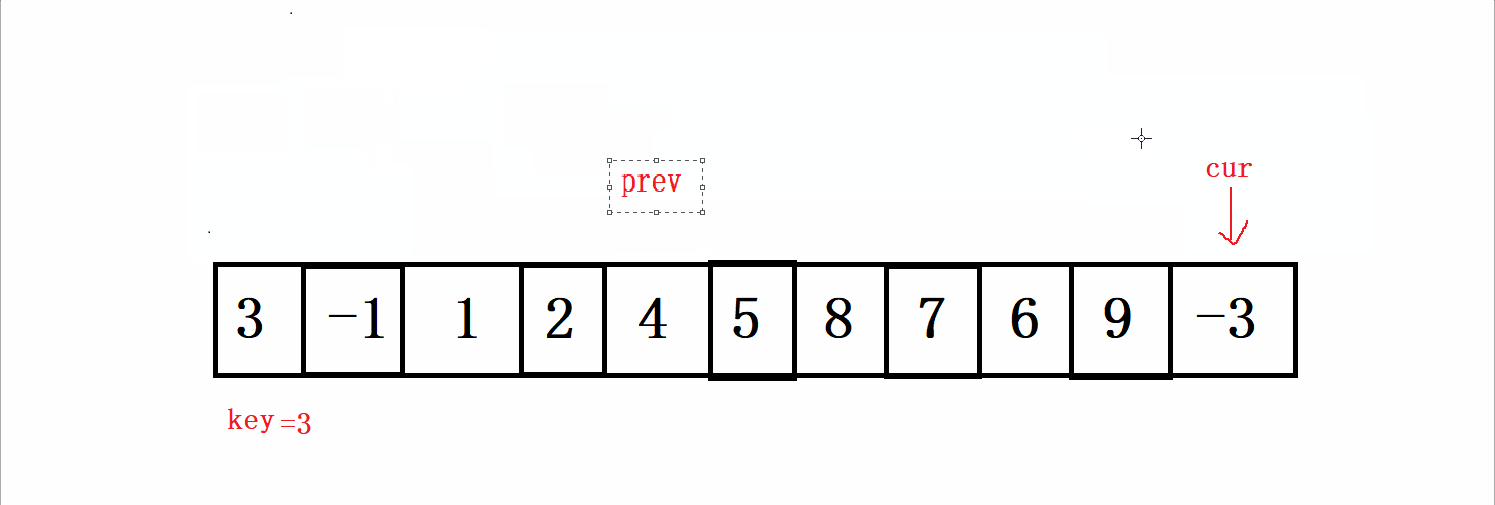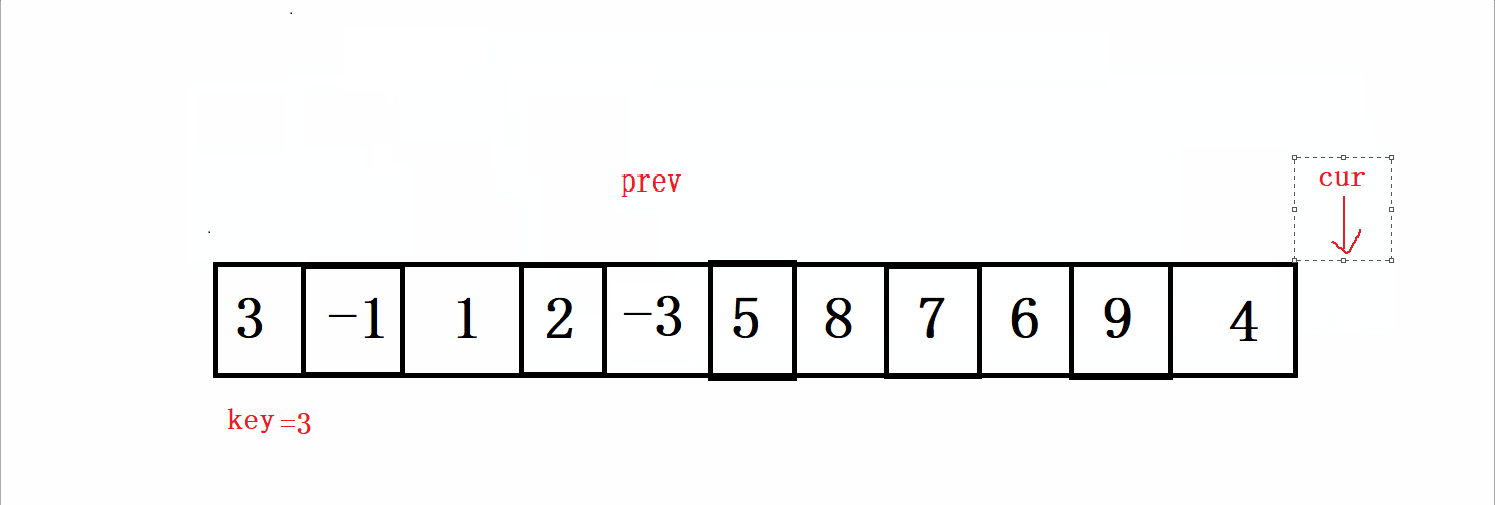
这一趟的循环结束之后,我们再交换,key和prev的值,结果如下:
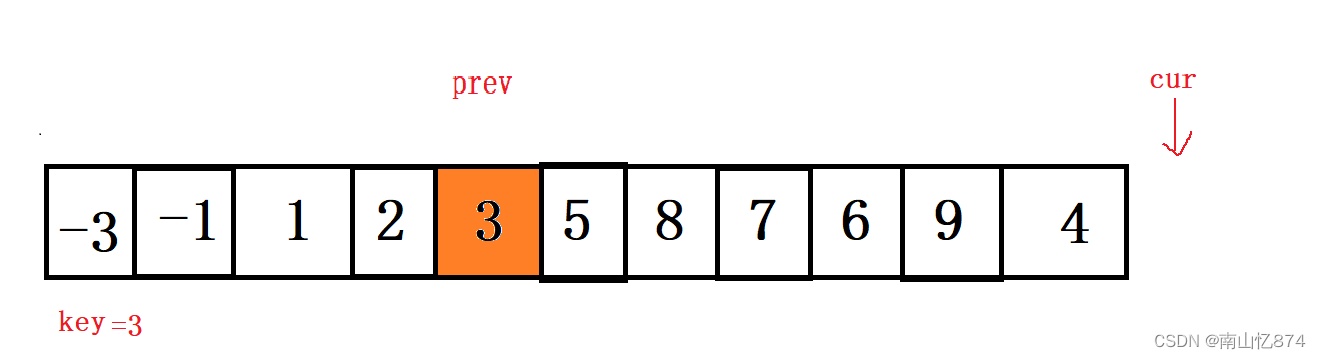
此时左边全是比key小的值,右边全是比key大的值,此时我们再以prev为中间值划分左右区间。
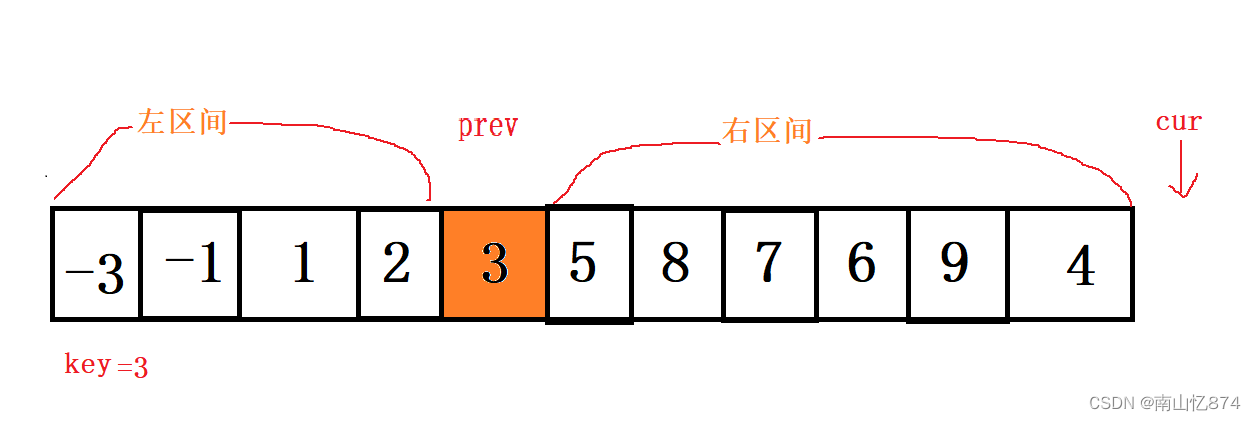
之后便是和前两种方式一样的去递归调用就好了。
三者的思路总体上来说,差别并不是很大,虽然有个别的差异,但是作为我们学习者来说益处还是很大的。
代码如下:
void quick2(int* a, int begin, int end)
{
if(begin >= end) return;
int key = begin;
int prev = begin;
int cur = begin;
while(cur <= end)
{
while(a[cur] < a[key] && ++prev != cur)
{
//满足条件,进行交换
Swap(&a[prev], &a[cur]);
}
cur++;
}
//每一次结束的最后一次交换
Swap(&a[key], &a[prev]);
quick2(a, begin, prev-1);
quick2(a, prev+1, end);
}
void Test()
{
int arr[] = {3,-1,1,2,4,5,8,7,6,9,-3};
int sz = sizeof(arr) / sizeof(arr[0]);
quick2(arr, 0, sz-1);
int i = 0;
for(; i < sz; ++i)
{
printf("%d ", arr[i]);
}
printf("\n");
}
int main()
{
Test();
return 0;
}
以上就是全部内容了,感谢支持!