写在前面：
首先感谢兄弟们的订阅，让我有创作的动力，在创作过程我会尽最大能力，保证作品的质量，如果有问题，可以私信我，让我们携手共进，共创辉煌。

路虽远，行则将至；事虽难，做则必成。只要有愚公移山的志气、滴水穿石的毅力，脚踏实地，埋头苦干，积跬步以至千里，就一定能够把宏伟目标变为美好现实。

“相似性度量（similarity measurement）”系列文章：、
【数据挖掘】机器学习中相似性度量方法-欧式距离
【数据挖掘】机器学习中相似性度量方法-余弦相似度
【数据挖掘】机器学习中相似性度量方法-曼哈顿距离
【数据挖掘】机器学习中相似性度量方法-切比雪夫距离

Hello，大家好。

继续更新"相似性度量（similarity measurement）"系列文章，今天介绍的是闵可夫斯基距离。多的不说，少的不唠，下面开始今天的教程。

以下内容，完全是我根据参考资料和个人理解撰写出来的，不存在滥用原创的问题。

闵可夫斯基距离

闵可夫斯基距离（Minkowski Distance），也称为闵氏距离，是一种在多维空间中衡量两点间距离的方法，它是对多个其他常见距离度量方法（如曼哈顿距离、欧式距离和切比雪夫距离）的一种概括和推广。闵可夫斯基距离可以将曼哈顿距离、欧式距离和切比雪夫距离总结为一个公式。

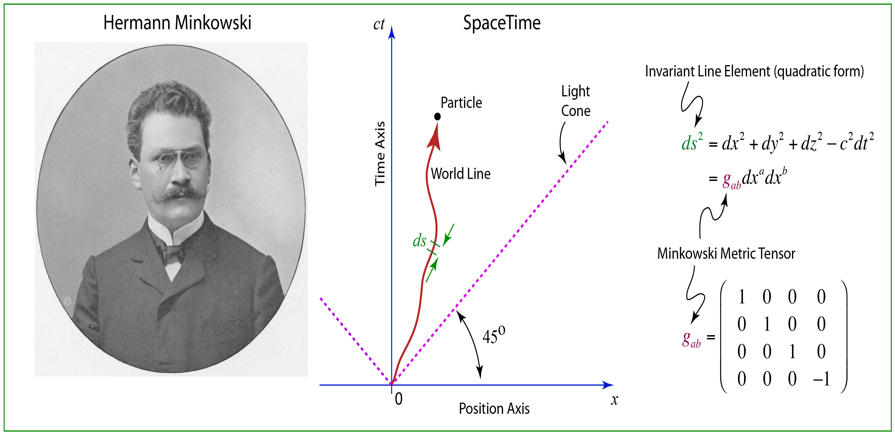
计算公式

两个向量或者两个点A($x_1,x_2,x_3,...,x_n$)和B($y_1,y_2,y_3,...,y_n$)之间的闵可夫斯基距离定义公式为：

$$d(A,B)={\left(\sum _{i=1}^n|x_i-y_i{|}^p\right)}^{\frac{1}{p}}$$

其中，p是一个正实数参数。

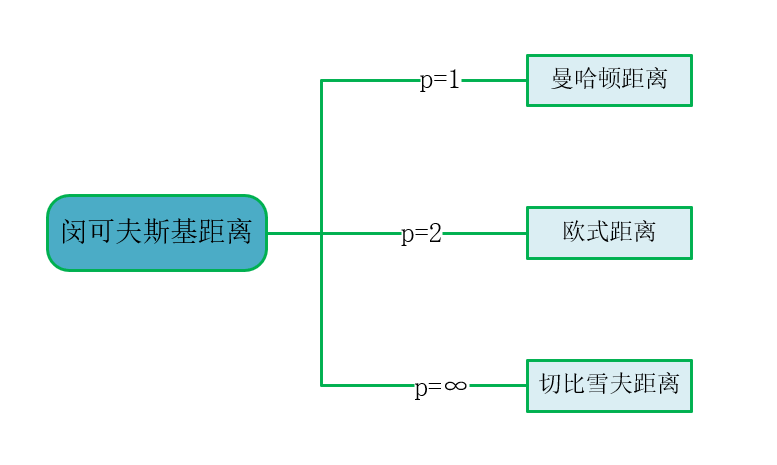
• 当p=1时，闵可夫斯基距离退化为曼哈顿距离（绝对距离、城市街区距离），即：
  $$d(A,B)=\sum _{i=1}^n|x_i-y_i|$$

• 当p=2时，闵可夫斯基距离退化为欧几里得距离（欧氏距离），即：
  $$d(A,B)=\sqrt{\sum _{i=1}^n(x_i-y_i{)}^2}$$

• 当p$\to \infty$时，闵可夫斯基距离变为切比雪夫距离（棋盘距离），即两点在各维度上距离的最大值：
  $$d(A,B)=\underset{p\to \infty }{\lim }{\left(\sum _{i=1}^n|x_i-y_i{|}^p\right)}^{\frac{1}{p}}=\max (|x_i-y_i|)$$

闵可夫斯基距离由于包含了多种距离度量，因此具有较广的适用范围。根据具体的应用场景和数据特性，可以选择合适的p值来定义距离。

代码实现

编写代码实现闵可夫斯基距离，下面是Python代码：

# -*- coding: utf-8 -*-
"""
Created on Sun Jun 23 16:45:37 2024

@author: AIexplore微信公众号
"""


import numpy as np  
  
def minkowski_distance(x, y, p=2):  
    """  
    计算两个点之间的闵可夫斯基距离  
      
    参数:  
    x, y: 数组或列表，代表两个点的坐标  
    p: 正实数，闵可夫斯基距离的指数  
      
    返回:  
    d: 闵可夫斯基距离  
    """  
    # 确保x和y是NumPy数组  
    x = np.array(x)  
    y = np.array(y)  
      
    # 检查x和y的维度是否相同  
    if x.shape != y.shape:  
        raise ValueError("输入的点必须具有相同的维度")  
      
    # 计算闵可夫斯基距离  
    diff = np.abs(x - y)  
    distance = np.sum(diff ** p) ** (1 / p)  
      
    return distance  
  
# data  
A = [1, 2, 3]  
B = [2, 3, 5]  
  
# 计算欧几里得距离 (p=2)  
euclidean_distance = minkowski_distance(A, B, p=2)  
print(f"欧几里得距离: {euclidean_distance}")  
  
# 计算曼哈顿距离 (p=1)  
manhattan_distance = minkowski_distance(A, B, p=1)  
print(f"曼哈顿距离: {manhattan_distance}")  
  
# 计算切比雪夫距离 (使用大的p值，例如1000，来近似)  
chebyshev_distance = minkowski_distance(A, B, p=10000)  # 注意：这不是严格的切比雪夫距离，近似  
print(f"切比雪夫距离近似: {chebyshev_distance}")

# 计算闵可夫斯基距离 (p=3)  
manhattan_distance = minkowski_distance(A, B, p=3)  
print(f"闵可夫斯基距离: {manhattan_distance}") 

输出结果：

欧几里得距离: 2.449489742783178
曼哈顿距离: 4.0
切比雪夫距离近似: 1.0000693171203765
闵可夫斯基距离: 2.154434690031884

参考文章

[1]https://blog.csdn.net/weixin_35757704/article/details/115437768
[2]https://mp.weixin.qq.com/s/g1-U59Xo7ScjscyrL61Ujw
[3]https://cloud.tencent.com/developer/article/2281505
[4]https://blog.csdn.net/qq_21484461/article/details/125357968

写在最后

作者介绍：CSDN人工智能领域优质创作者，CSDN博客专家，阿里云专家博主，阿里云技术博主，有机器学习、深度学习、OCR识别项目4年以上工作经验，专注于人工智能技术领域。会根据实际项目不定期输出一些非商业的技术，内容不限，欢迎各位朋友关注。
1、关注下方公众号，让我们共同进步。
2、需要技术指导、交流合作，点击"关于我-与我联系"添加微信交流。

都看到这里了，动动发财的小手点个赞再走吧。

微信扫码关注微信公众号，发现不一样的世界。