Linux_软硬链接

news2025/1/16 14:04:44

1、软链接

2、软链接的使用方式

3、软链接的删除

4、硬链接

5、硬链接的使用方式

6、软硬链接的使用场景

7、软硬链接的区别

结语

前言：

在Linux操作系统中，有软链接和硬链接，他们是一种特殊的文件引用，主要用于与目标文件建立链接关系从而生成新的链接文件，并且访问该链接文件就能访问目标文件，给用户提供了多种访问文件的途径，方便了用户的使用，合理使用软硬链接能够有效的提高系统的效率。

1、软链接

软链接所生成的链接文件是一个独立的文件，该链接文件中保存的是目标文件的路径，他仅仅是一个快捷方式，文件内并不包含目标文件的内容。为什么说软链接生成的文件是一个独立的文件呢？因为该文件的文件标识符inode是唯一的，和目标文件的标识符不一样，如下图：

生成软链接文件的指令：

ln -s 目标文件（可以是目录） 链接文件的名称
// -s表示创建的链接文件是软链接

创建一个软链接：

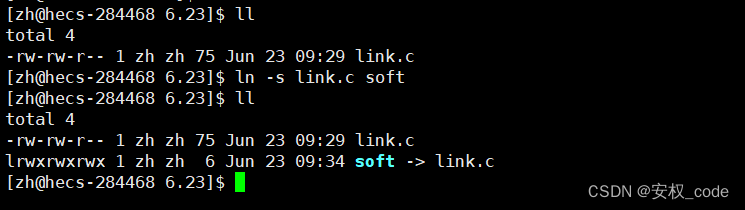
可以看到soft就是一个软链接文件，通过箭头可以发现他指向的文件是link.c，所以通过操作soft来间接的操作link.c。

2、软链接的使用方式

比如cat软链接文件就是cat 目标文件：

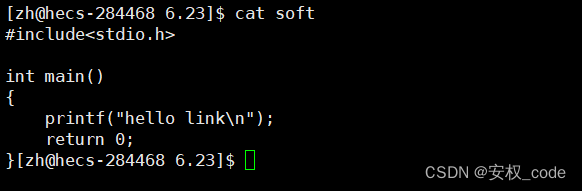
当然快捷方式的存在意义就是直接通过运行快捷方式来运行程序本身，所以软链接一般链接的都是可执行程序，达到运行软链接文件即运行目标可执行程序的效果，测试如下：

并且也可以通过软链接文件更改目标文件的内容：

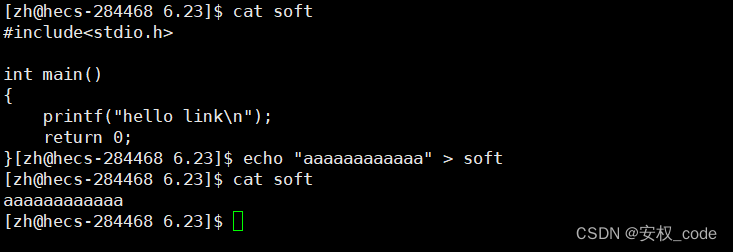
3、软链接的删除

若把目标文件删除，则软链接就不可用了，即无法对软链接进行以上的使用方式：

此时soft链接文件就没有意义了，可以使用指令unlink对其删除：

unlink 要删除的链接文件

测试结果：

4、硬链接

如果说软链接像一个指针指向目标文件，那么硬链接就是目标文件的“别名”，他和软链接不一样的是硬链接所产生的链接文件和他指向的目标文件用的是同一块数据块，即他们的inode是相同的。

生成硬链接文件的指令：

ln 目标文件 硬链接文件的名称

测试硬链接如下：

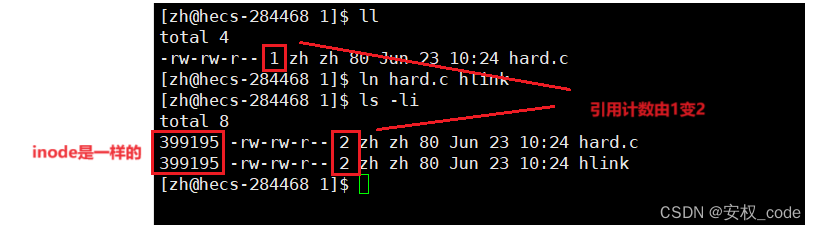
观察结果得到一个结论，两个文件的inode是一样的，说明链接文件是目标文件的“别名”，即可以把链接文件当作是目标文件的本体，并且对一个文件使用硬链接后会使目标文件和链接文件的引用计数都变成2，引用计数为2表示删除其中任意一个文件只会导致引用计数减1，并不会影响另一个文件的使用。

结语：文件名只是方便用户查看文件则系统所使用的方法，实际上系统是根据inode来区分文件的，因此上图中hard.c这个文件名并不能表示底层真实的文件，他类似文件的外壳，inode才是用于标记底层文件的真实身份，所以399195才是文件本体，而上图中删除hard.c这个动作并没有把底层的真实文件删除，只是删除了其外壳（因为他进行了硬链接），399195文件依然存在并且可以访问和使用。

5、硬链接的使用方式

软链接可以做到的使用方式硬链接也都可以做到，比如cat链接文件在上文中已经验实，硬链接的文件也可以通过编译生成可执行程序：

并且也可以通过修改链接文件从而修改目标文件：

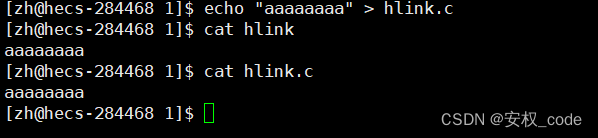
6、软硬链接的使用场景

硬链接的使用场景：

1、由于硬链接是共用同一个inode，意味着硬链接不会创建新文件，则硬链接有着节省内存空间的优势，在需要拷贝一些较大的文件时可以使用硬链接代替拷贝。

2、备份文件时也可以使用硬链接产生的链接文件作为备份。

软链接的使用场景：

1、在一些程序的路径非常深的场景下，软链接则无需进入那么深的路径也可以直接运行程序。

2、面对一些可能会随时更改路径的文件，软链接则可以保证随时都能找到他们。

3、多个目录需要共用一个文件时，无需把该文件在每个目录下都拷贝一份，在各个目录下使用软链接指向该文件即可。

7、软硬链接的区别

1、硬链接生成的文件和目标文件inode相同，软链接生成的文件和目标文件inode不同。

2、硬链接不能连接目录（因为系统在遍历文件时会导致循环引用，从而破坏文件系统的结构），软链接可以连接目录。

3、删除硬链接的目标文件，则连接文件依旧可以正常使用，若删除软链接的目标文件，则连接文件不能正常使用了。

4、硬链接文件不占内存，软链接文件占用若干字节内存。

5、硬链接不能跨越不同的文件系统（因为每个inode是特定于系统的，而硬链接直接和inode打交道），软链接可以。

6、软链接可以使用绝对路径和相对路径（因为软链接保存的是目标文件的路径），硬链接只能使用绝对路径（因为硬链接保存的是inode，系统用inode遍历文件用的是绝对路径）。

7、软链接的指令是ln -s，硬链接是ln。