一、什么是树
数据结构中的树是一种非常重要的非线性数据结构。它由节点(Node)和边(Edge)组成,用于表示具有层次关系的数据。
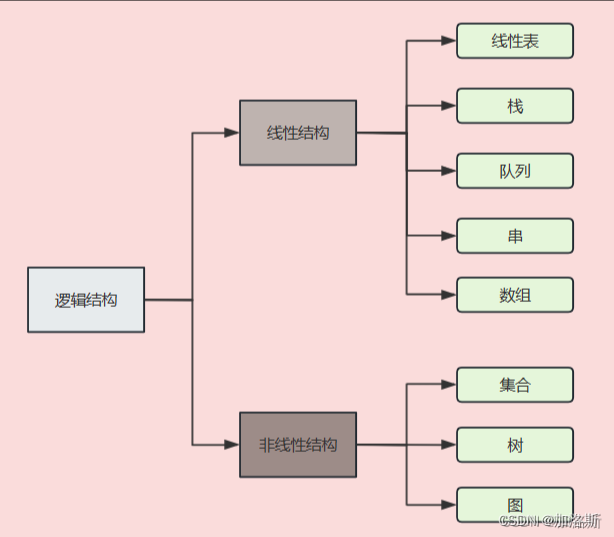
1.1、树的基本概念
- 节点(Node):
- 树的基本单位,每个节点包含一个值(或称为键)和若干子节点的引用。
- 根节点(Root Node):树的顶点,没有父节点。
- 叶节点(Leaf Node):没有子节点的节点。
- 边(Edge):
- 节点之间的连接,表示节点之间的关系。
- 子节点(Child Node)和父节点(Parent Node):
- 子节点是直接连接在某个节点下的节点。
- 父节点是直接连接某个节点上的节点。
- 深度(Depth):
- 节点的深度是从根节点到该节点的边的数量。
- 高度(Height):
- 节点的高度是从该节点到叶节点的最长路径的边的数量。
- 树的高度是根节点的高度。
- 度(Degree):
- 节点的度是其子节点的数量。
- 树的度是所有节点中最大的度。

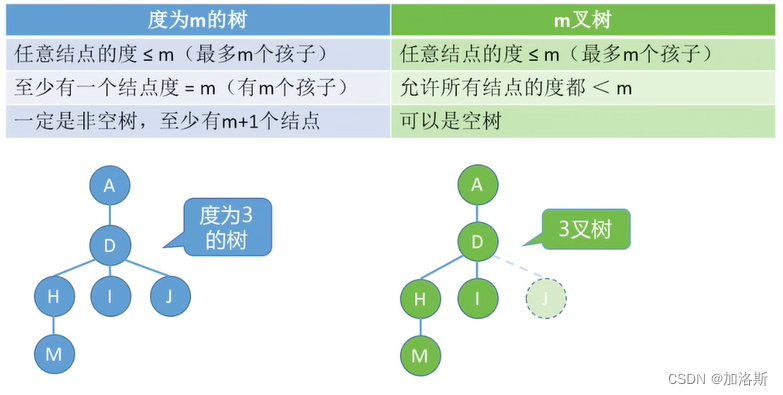
问题1:对于度为m的树,与m叉树有什么区别?
- 答:
树的度就最大节点的度,节点的度就是节点有多少个孩子节点,度为m的树,其至少有一个节点的孩子数量为m。
而m叉树不同,m叉树是我们规定其子节点最多为3个,实际上并不要求其一定为3个,它不仅可以不为3,实际上他没有节点,是个空树都可以。
1.2、树的分类
-
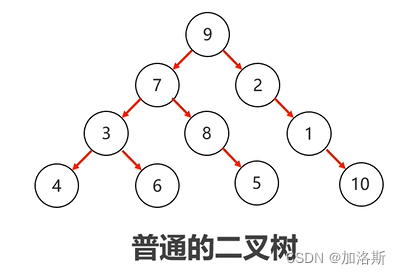
二叉树:
- 每个节点最多有两个子节点,分别称为左子节点和右子节点。
-
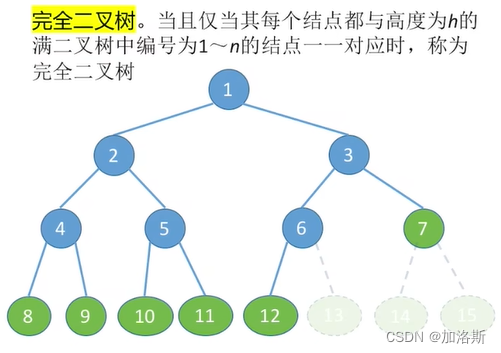
完全二叉树:
- 除了最后一层,其他每一层的节点都是满的,最后一层的节点从左到右排列。
-
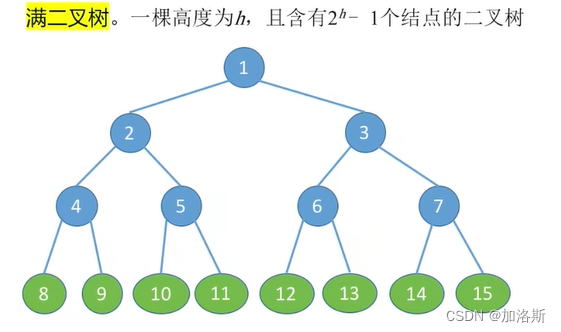
满二叉树:
- 每个节点要么是叶节点,要么有两个子节点。
-
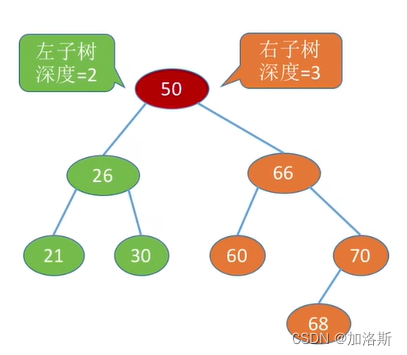
平衡二叉树:
- 任意节点的两个子树的高度差不超过1。例如:AVL树、红黑树。
-
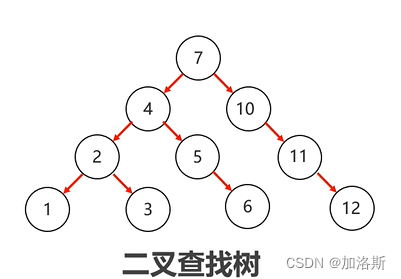
二叉搜索树:
- 对于每个节点,左子树上所有节点的值小于该节点的值,右子树上所有节点的值大于该节点的值。
-
多叉树(Multi-way Tree):
- 每个节点可以有多于两个的子节点。
二、二叉树
2.1、二叉树的基本知识
二叉树是一种每个节点最多有两个子节点的树形数据结构。他一般有五种状态。
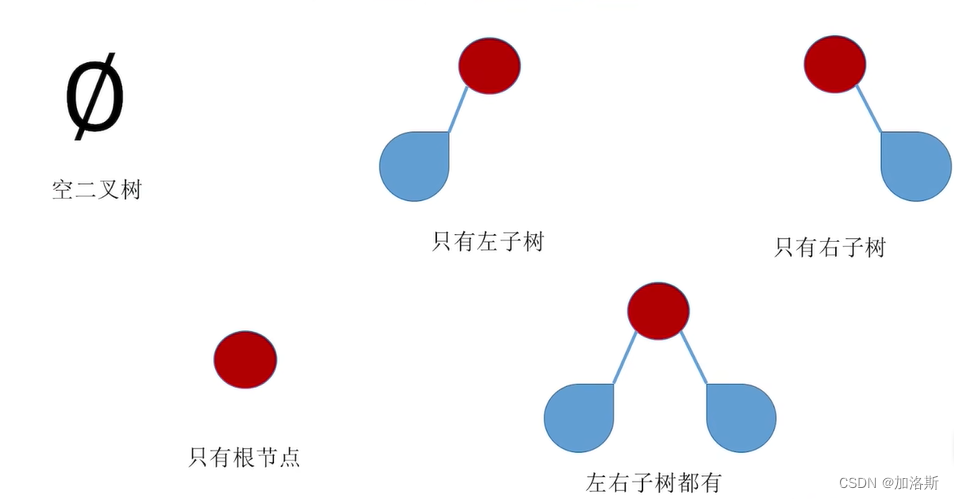

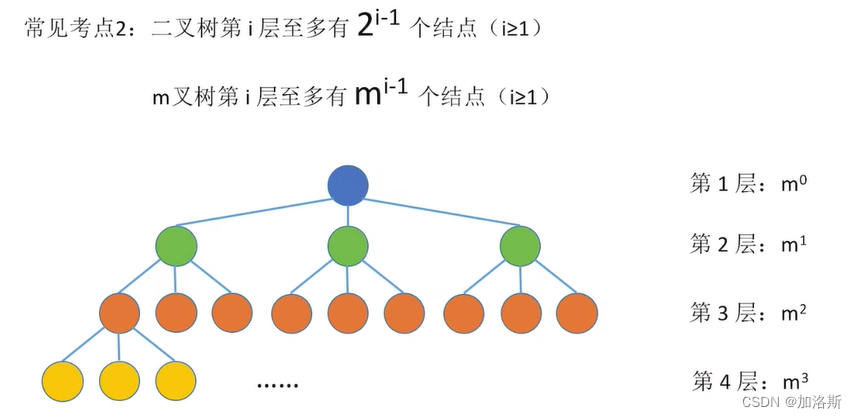
这其中对我们最为有帮助的就是二叉查找树。
2.2、二叉查找树
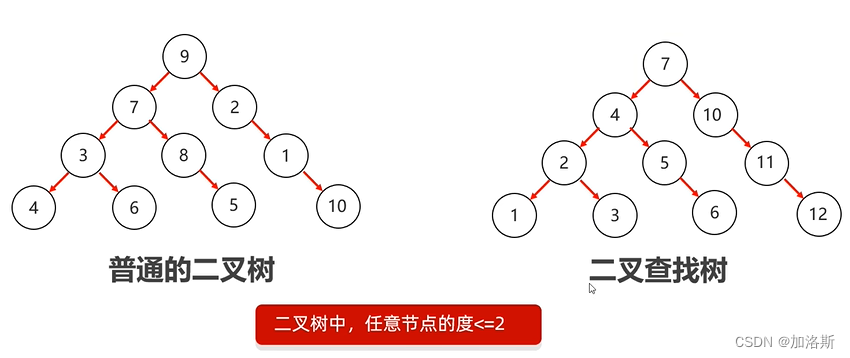
通过上图我们可以看到,在二叉查找树中,任意节点中,左节点一定小于父节点,而右节点一定大于父节点。而通过根节点来看,根节点其左子树上元素统统小于根节点,相反右子树上所有元素都大于根节点。
2.3、遍历
二叉树有四种遍历方式:前序遍历、中序遍历、后序遍历,层序遍历。

2.3.1、前序遍历
从根结点开始,然后按照当前结点,左子结点,右子结点的顺序遍历。
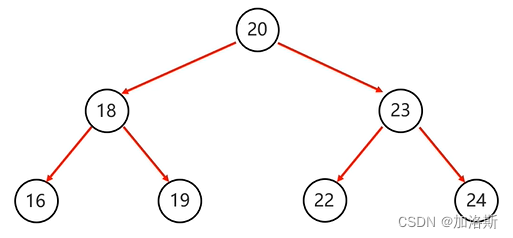
其前序遍历顺序为:20、18、16、19、23、22、24
2.3.2、中序遍历
从最左边的子节点开始,然后按照左子结点,当前结点,右子结点的顺序遍历。
中序遍历是最重要的一种,其在平衡二叉树中遍历结果就是从小到大的。

其中序遍历顺序为:16、18、19、20、22、23、24
2.3.3、后序遍历
从最左边的子节点开始,然后按照左子结点,右子结点,当前结点的顺序遍历

其中序遍历顺序为:16、19、18、22、24、23、20
2.3.4、层序遍历
一层一层遍历

其中序遍历顺序为:20、18、23、16、19、22、24
三、平衡二叉树
3.1、平衡二叉树基本知识
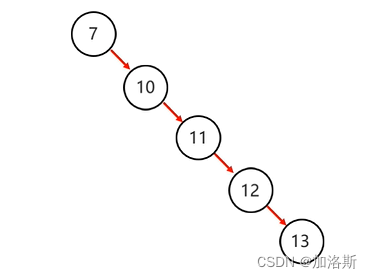
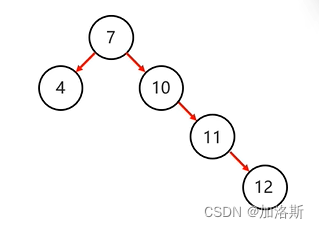
思考一个问题,按照二叉树的规则,将7、10、11、12、13插入到一颗树中,其结构图如下:
是不是看着非常的难受?这右边太长了!!所以引出了平衡二叉树的概念。
平衡二叉树就任意节点左右子树高度相差不大于1。
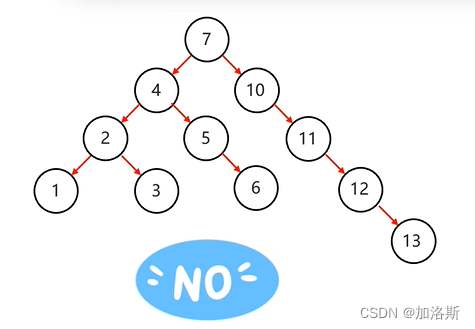
在10节点,其左子树高度为0,右子树高度为3,不满足平衡二叉树。
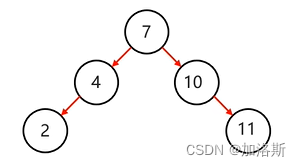
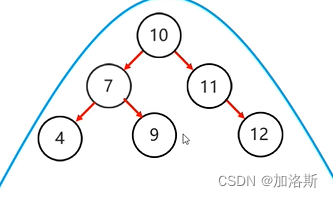
这是一个标准的平衡二叉树。
3.2、平衡二叉树旋转知识
平衡二叉树的左右子树高度不超过1,极大地提高了查找的效率,那么如何保证其左右子树高度不超过1呢?
保证平衡二叉树的根本在于旋转,分为左旋与右旋。但是不是每次插入都会触发旋转,只有打破了平衡二叉树才会进行旋转。
那么如何判断是左旋还是右旋呢?
当我们按照规则添加一个元素后打破了平衡树,此时我们向添加元素的父节点向上寻找,找到第一个不平衡的节点,作为
支撑节点。如图
在添加了12后,平衡树被打破,此时寻找支点,父节点11还是平衡二叉树,向上寻找父节点10,发现10节点不为平衡二叉树,10就作为支点。
同时,10的右边比左边多,所以进行左旋。
在来看一个左旋的例子
同理,右旋步骤与左旋相同。
四、红黑树
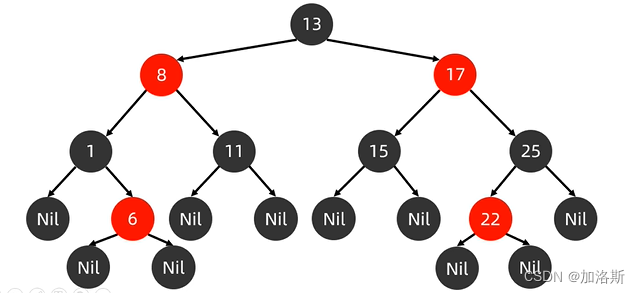
红黑树是一种特殊的二叉查找树,红黑树的每一个节点上都有存储位表示节点的颜色。每一个节点可以是红或者黑,红黑树不是高度平衡的,它的平衡是通过"红黑规则"进行实现的。
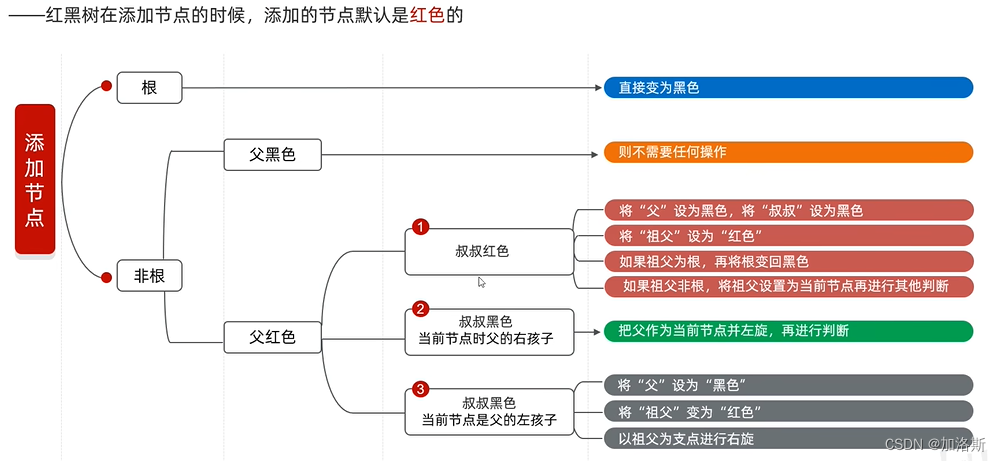
红黑规则: