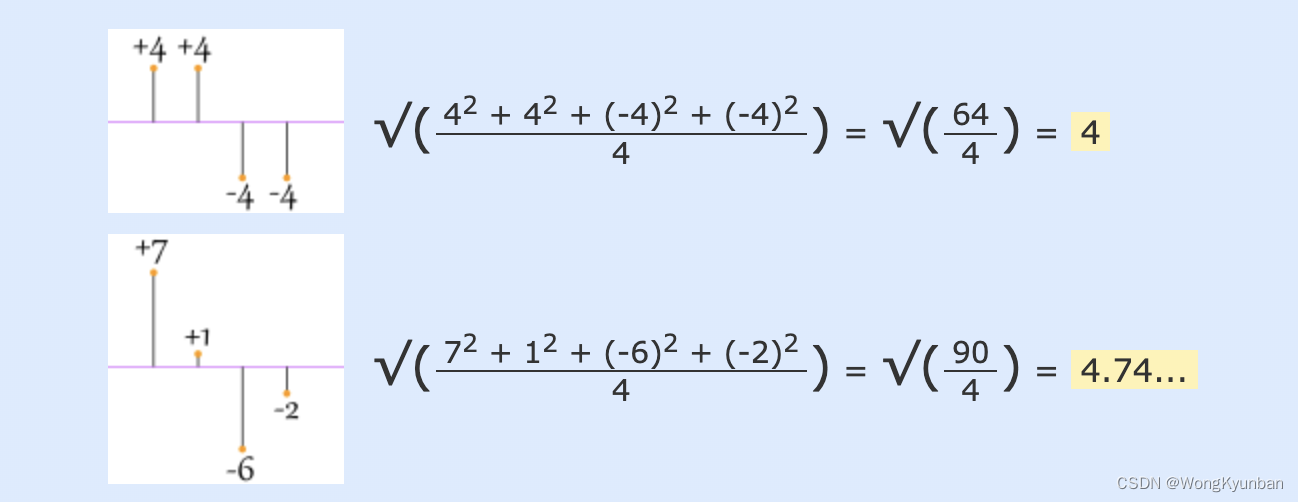标准差是用于衡量数字是如何分布的指标。用σ （sigma）表示。
标准差=方差的平方根。

什么是方差

方差就是与均值的平方差的平均值。方差的计算过程：

1. 计算平均值（mean）用μ /读mu/表示。
2. 用每一个数减去平均值，再平方（对差进行平方）
3. 将第二步得到的平方值都加起来，再除以数据的个数，就能得到方差。

方差的求值公式：

$${\sigma }^2=\frac{1}{N}\sum _{i=1}^n(x_i-\mu {)}^2$$

μ：表示平均值

标准差

标准差就是对方差进行开方
$$\sigma =\sqrt{{\sigma }^2}$$

一般来说，我们都会直接求标准差，因为标准差用得比较多：
$$\sigma =\sqrt{\frac{1}{N}\sum _{i=1}^n(x_i-\mu {)}^2}$$
​
有了标准差后，我们就有了一个“标准”的方式去识别哪些数据是正常的，哪些数据是过大，哪些数据是过小的。为什么可以这样呢？
首先，标准差是每个数据点到平均值这个点的最小距离之和的平均，描述了平均下来，每个点到平均值点的距离，以此来说明数据的分布情况。平均值点这个位置就是标准，有了标准差后，就可以用这个值去衡量具体的数据点是过大还是过小，抑或是正常的。

举个例子来说吧：
10个同学的身高(cm)分别为：150,130,160,185,135,168,170,155,120,169

$$平均值=\frac{150+130+160+185+135+168+170+155+120+169}{10}=154.2$$

$$方差=\frac{(150-154.2{)}^2+(130-154.2{)}^2+(160-154.2{)}^2+(185-154.2{)}^2+(135-154.2{)}^2+(168-154.2{)}^2+(170-154.2{)}^2+(155-154.2{)}^2+(120-154.2{)}^2+(169-154.2{)}^2}{10}=378.36$$

$$标准差=\sqrt{3}78.35=19.45147809$$

10个数据点的分布情况：

我们有了一个标准差后，我们就有了一个标准的方式去判断哪些同学的身高是太高或太小，或正常。在我们这个实例中，如果我们认为在一个标准差内的身高属于正常范围，那么120，133都显得太矮小了，185就太高了。

上面这个例子是针对10个同学的身高的（也就是说我们只对这10个同学的身高感兴趣，样本空间都是在这了）。

样本标准差

但是，如果数据是样本（从更大的总体中选择），则计算会发生变化！即10个同学的身高是一个样本数据（我们现在感兴趣的是全校同学的身高），因为有时候样本空间太大，不方便操作，我们可以通过样本来评价总体。计算样本标准差就与前面的会有所不同：

$$s=\sqrt{\frac{1}{N-1}\sum _{i=1}^n(x_i-\bar{x}{)}^2}$$

s：代表样本标准差
样本标准差的计算过程与前面无异，唯一的区别就是前面是除以N，这里是除以N-1，

$$方差=\frac{(150-154.2{)}^2+(130-154.2{)}^2+(160-154.2{)}^2+(185-154.2{)}^2+(135-154.2{)}^2+(168-154.2{)}^2+(170-154.2{)}^2+(155-154.2{)}^2+(120-154.2{)}^2+(169-154.2{)}^2}{10-1}=420.4$$

$$标准差=\sqrt{4}20.4=20.50365821$$
样本标准差得到的结果与实际很接近了。为什么要除以N-1而不是除以N呢？当年确实时除以N的，只是当时的人发现样本空间的数据除以N后得到的值往往都比实际的要小，于是想办法纠偏，就想到了一个简单的办法就是少除一个，这样结果就不会太小了，大一些也无所谓。

为什么要对每个差值进行平方，取绝对值不行吗？

$${\sigma }^2=\frac{1}{N}\sum _{i=1}^n(x_i-\mu {)}^2$$

首先，各个数据点与平均值点的距离是不能直接相加的，因为有可能会出现正负抵消的情况，这就没有办法客观表示点与点之间的距离了。如 下图：

那么，直接取它们的差值的绝对值作为两点之间的距离呢？下面两张图都用了绝对值的办法，都得到了相同的值，可是这个值反映不出两个组数据的分布情况，相同的值应该对应类似的数据分布，但是从下面两张图可知，它们各自数据的分布是有很大不同的，但是无法反映出来。

为什么在计算标准时用平方数据点与平均值点的差，可以客观反映数据的分布特点呢？
首先，平方数据差，可以避免正负相加，互相抵消的问题。其次这种方式是很类似于欧几里德空间里的两点之间的距离的计算的。当数据差异更加分散时，标准差会更大…而这正是我们想要的。

还有一点在平方和平方根上使用代数比在绝对值上更容易。有时候数值的准确性并不是必要的，能说明和反映问题才是必要的，这个思想很重要。