【动态规划】1130. 叶值的最小代价生成树

news2024/11/27 2:16:01

1130. 叶值的最小代价生成树

难度：中等
力扣地址：https://leetcode.cn/problems/minimum-cost-tree-from-leaf-values/description/

题目内容

给你一个正整数数组 arr，考虑所有满足以下条件的二叉树：

每个节点都有 0 个或是 2 个子节点。
数组 arr 中的值与树的中序遍历中每个叶节点的值一一对应。
每个非叶节点的值等于其左子树和右子树中叶节点的最大值的乘积。
在所有这样的二叉树中，返回每个非叶节点的值的最小可能总和。这个和的值是一个 32 位整数。

如果一个节点有 0 个子节点，那么该节点为叶节点。

示例 1：
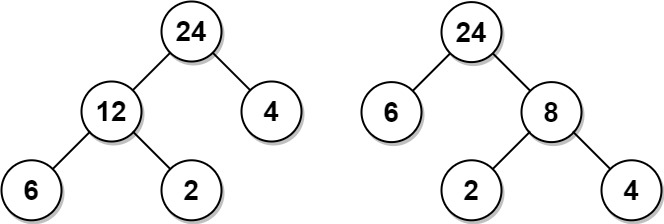
在这里插入图片描述

输入：arr = [6,2,4]
输出：32
解释：有两种可能的树，第一种的非叶节点的总和为 36 ，第二种非叶节点的总和为 32 。

示例 2：
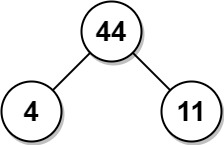
在这里插入图片描述

输入：arr = [4,11]
输出：44

提示：

2 <= arr.length <= 40
1 <= arr[i] <= 15
答案保证是一个 32 位带符号整数，即小于 $2^{31}$ 。

解题过程 1 —— 小白的思考流程

由于本人能力有限，木有做出来。此处主要参考了官方的解题过程，结合自己的理解记录一下。

题目看起来很复杂，实际上也不简单。这里我们首先使用比较直观的方法求解：列举所有可能，并起初结果，然后返回最小的。如例1所示，这里我们先把两种情况画出来，就知道哪个结果更小了。

即：输入 6 2 4 时，有可能的结果是 6 * 4 + 2 * 4 = 32；也有可能是 6 * 4 + 2 * 6 = 36。这里我们定义一个函数，用来求解三个结点时的最优结果。

int calculate(int a, int b, int c) {
    // 如果 d1 较小，则选择让 a 与 b 结合，成为兄弟结点
    int d1 = (a * b) + max(a, b) * c;

    // 如果 d2 较小，则选择让 b 与 c 结合，
    int d2 = (b * c) + max(b, c) * a;
    return min(d1, d2);
}

接着我们需要思考的问题是，如果超过3个结点，该如何应对？

比如现在的输入是 [6,4,5,1]，最终的结果是 55，计算方法是

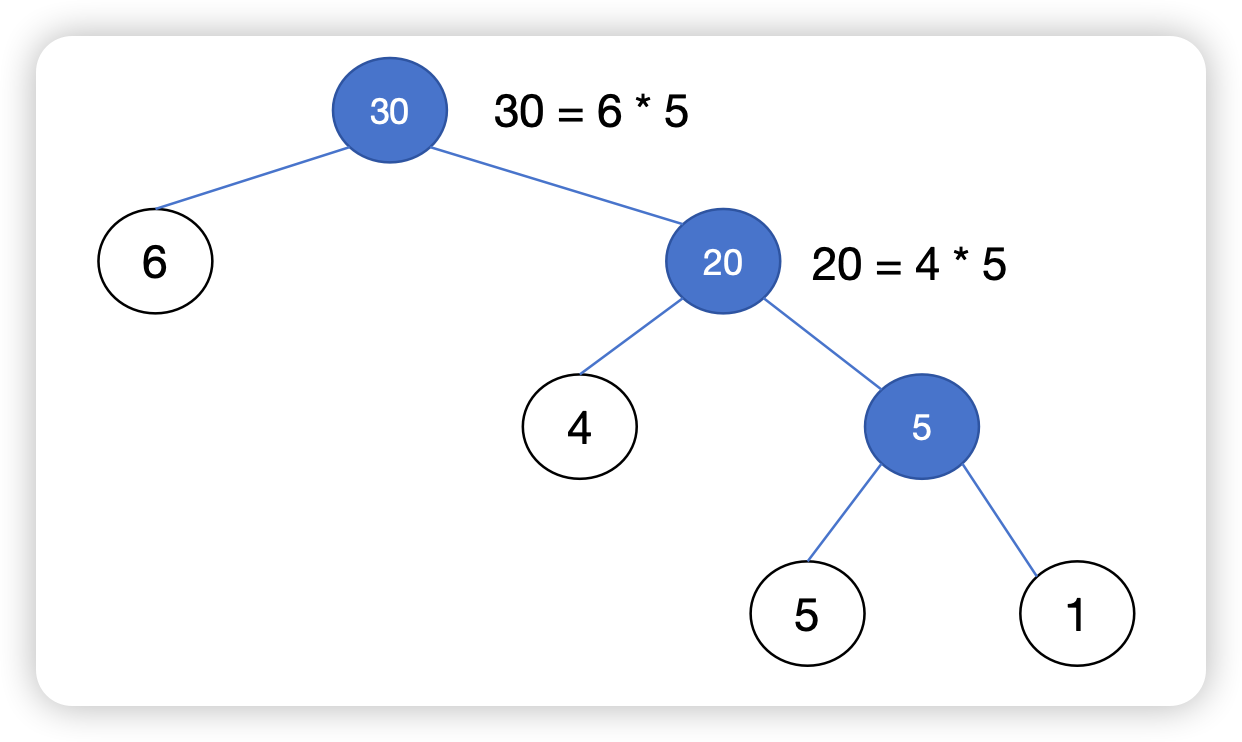
在这里插入图片描述

这种情况下，我们发现 5 和 1 是兄弟结点，然后 5与1 的结合结果与 4 是兄弟结点，而 6 与它们仨的结合体是兄弟节点。

这里我们应当把其他情况也列一下：

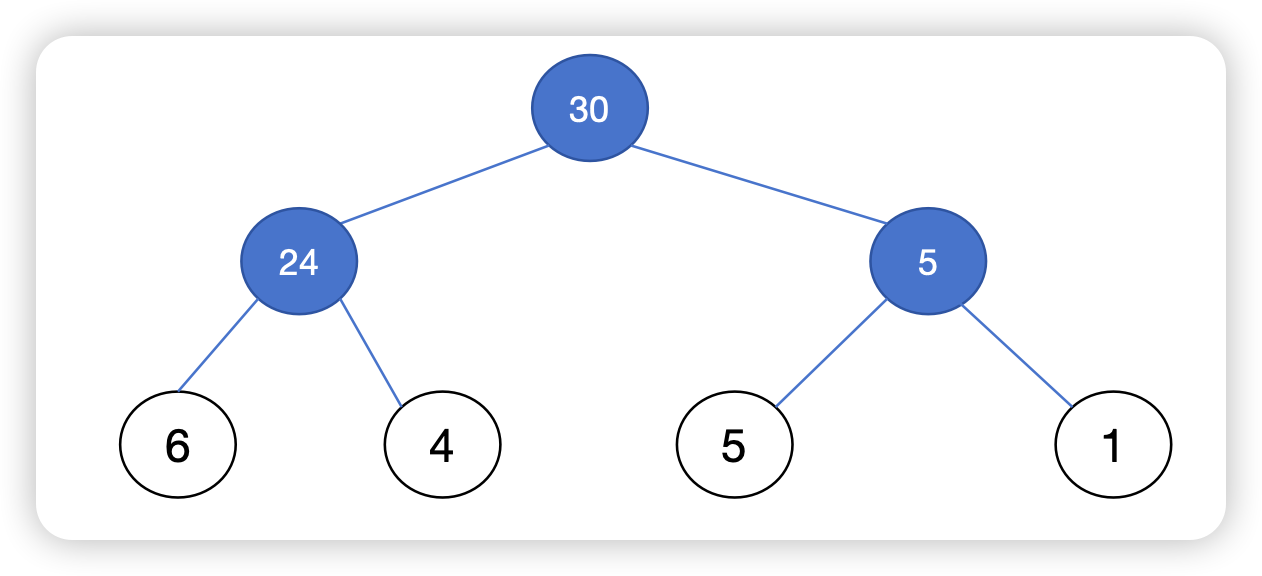
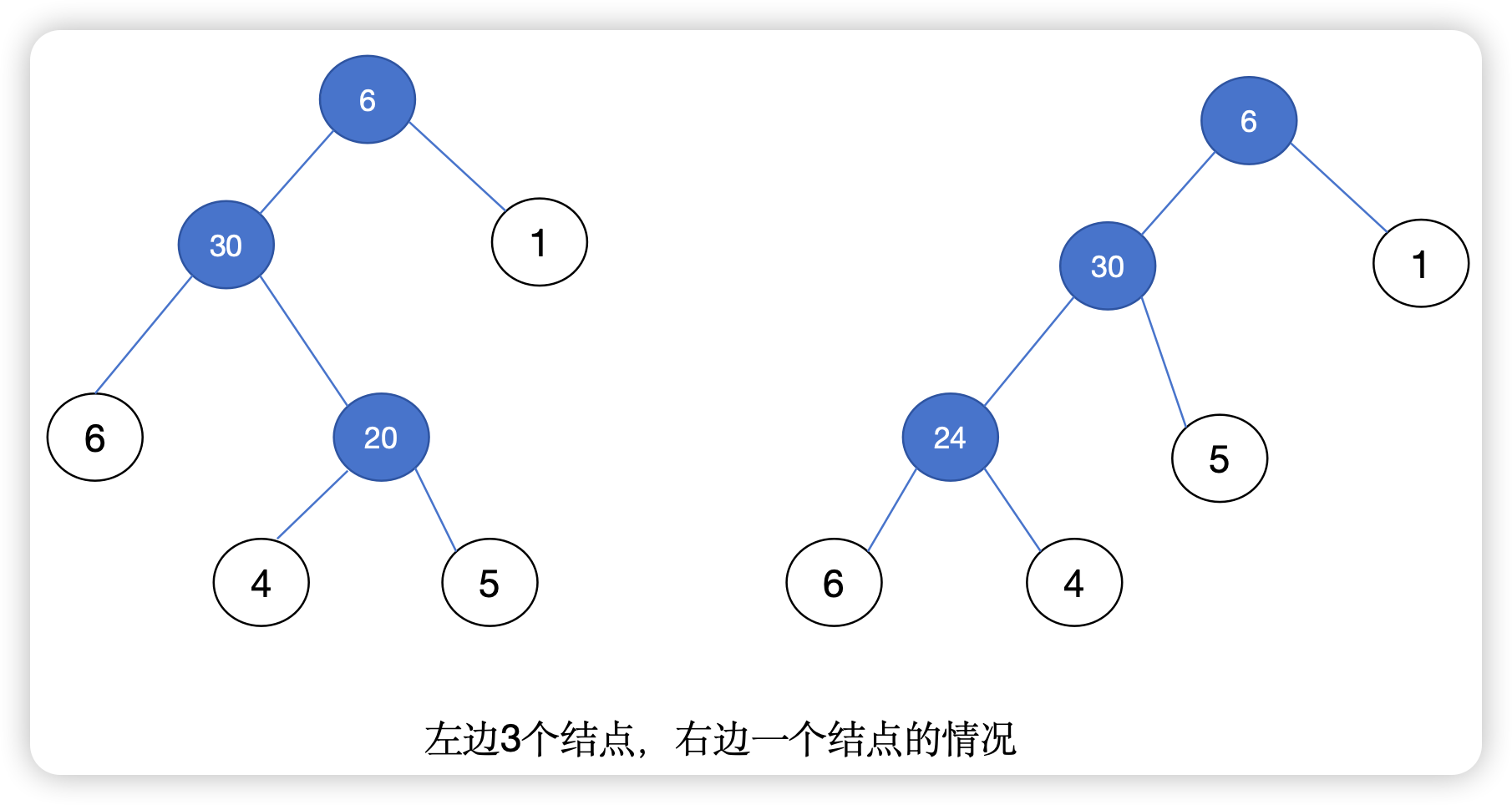
在这里插入图片描述

这个时候我们可以发现，这些结果也就是 calculate(a, b, c) 得到结果 d1 然后再将 d1 与 d 重新计算；或者计算 calculate(b, c, d) 得到 d2，然后再计算 d2 与 a 的结果。

结论1：总而言之，我们需要划分，也就是分治过程。

接下来我们可以开始处理更加复杂的情况了，如果总共有 5 个结点，我们可以先将前3个看为一个整理，然后与第4个与第5个计算得到结果；也可以 ……

这里我们直接强行计算所有情况。

接下来需要考虑，左右子树的划分过程，前面给出的例子中，[6, 4, 2, 1] 可以分为三种情况，1 + 3（左子树1个，右子树3个），2 + 2 （左右子树各一个）以及 3 + 1 （左子树3个，右子树1个）。

类似地，如果更多结点，我们需要考虑这种左右子树的划分过程，并且根据每种情况计算结果。

结论2：需要考虑所有的左右子树划分情况（循环遍历所有可能）。

开始写代码：

class Solution {
public:
    int mctFromLeafValues(vector<int>& arr) {
        int n = arr.size();
        // dp[i][j] 表示从 arr[i] 到 arr[j] 构成的子树的非叶节点值的最小总和
        vector<vector<int>> dp(n, vector<int>(n, INT_MAX / 4));
        // maxVal[i][j] 表示从 arr[i] 到 arr[j] 之间的最大值
        vector<vector<int>> maxVal(n, vector<int>(n));
        for (int j = 0; j < n; j++) {
            // 计算 arr[i] 到 arr[j] 之间的最大值。
            // maxVal[i][j - 1] 是子数组 arr[i] 到 arr[j-1] 的最大值。
            // 新加入的元素是 arr[j]，所以 maxVal[i][j] 是 maxVal[i][j - 1] 和 arr[j] 中的较大值。
            // 当只有一个元素时，最大值就是元素本身
            maxVal[j][j] = arr[j];
             // 单个节点没有非叶节点，值为 0
            dp[j][j] = 0;
            for (int i = j - 1; i >= 0; i--) {
                // 更新 maxVal[i][j] 为子数组 arr[i] 到 arr[j] 的最大值
                maxVal[i][j] = max(arr[i], maxVal[i + 1][j]);
                // 枚举分割点 k，将子数组分为 arr[i] 到 arr[k] 和 arr[k + 1] 到 arr[j]
                for (int k = i; k < j; k++) {
                    // 更新 dp[i][j] 为分割后子树的最小非叶节点值总和
                    dp[i][j] = min(dp[i][j], dp[i][k] + dp[k + 1][j] + maxVal[i][k] * maxVal[k + 1][j]);
                }
            }
        }
        return dp[0][n - 1];
    }
};

时间复杂度： $O(n^3)$
空间复杂度： $O(n^2)$

方法总结：

动态规划的核心 在于通过解决子问题来解决更大规模的问题。我们通过定义 dp[i][j] 来表示子数组 arr[i] 到 arr[j] 的最小非叶节点值的总和，这样我们可以逐步从小规模问题解决到大规模问题。
分治法的核心思想 是将一个大问题分解成若干个小问题分别解决，然后将小问题的解组合成大问题的解。在这个问题中，我们通过枚举分割点 k 来将子数组 arr[i] 到 arr[j] 分成两部分，即 arr[i] 到 arr[k] 和 arr[k+1] 到 arr[j]，然后分别解决这两部分子问题，最后将它们的解组合起来。

具体来说，分治思想体现在：

分解：将子数组 arr[i] 到 arr[j] 分成两部分，即 arr[i] 到 arr[k] 和 arr[k+1] 到 arr[j]。
解决：分别解决这两个子问题，即计算 dp[i][k] 和 dp[k+1][j]。
合并：将两个子问题的解 dp[i][k] 和 dp[k+1][j] 合并，同时加上当前划分下的非叶节点值 maxVal[i][k] * maxVal[k+1][j]。