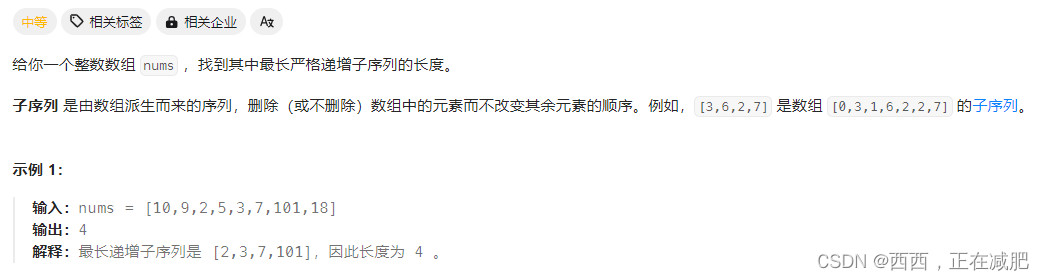
300.最长递增子序列
力扣链接
==动规五部曲 ==
- dp的定义
dp[i]表示子序列答案以nums[i]结尾的最长递增子序列的长度
为什么一定表示 “以nums[i]结尾的最长递增子序” ,因为我们在 做 递增比较的时候,如果比较 nums[j] 和 nums[i] 的大小,那么两个递增子序列一定分别以nums[j]为结尾 和 nums[i]为结尾, 要不然这个比较就没有意义了,不是尾部元素的比较那么 如何算递增呢。- 状态转移方程:
位置i的最长升序子序列等于j从0到i-1各个位置的最长升序子序列 + 1 的最大值。
所以:if (nums[i] > nums[j]) dp[i] = max(dp[i], dp[j] + 1);
- dp初始化
每一个i,对应的dp[i](即最长递增子序列)起始大小至少都是1- 确认遍历顺序:
dp[i] 是有0到i-1各个位置的最长递增子序列 推导而来,那么遍历i一定是从前向后遍历。
j其实就是遍历0到i-1,那么是从前到后,还是从后到前遍历都无所谓,只要吧 0 到 i-1 的元素都遍历了就行了。 所以默认习惯 从前向后遍历。
遍历i的循环在外层,遍历j则在内层
DP
class Solution:
def lengthOfLIS(self, nums: List[int]) -> int:
if len(nums) <= 1:
return len(nums)
dp = [1] * len(nums)
result = 1
for i in range(1, len(nums)):
for j in range(0, i):
if nums[i] > nums[j]:
dp[i] = max(dp[i], dp[j] + 1)
result = max(result, dp[i]) #取长的子序列
return result
贪心
class Solution:
def lengthOfLIS(self, nums: List[int]) -> int:
if len(nums) <= 1:
return len(nums)
tails = [nums[0]] # 存储递增子序列的尾部元素
for num in nums[1:]:
if num > tails[-1]:
tails.append(num) # 如果当前元素大于递增子序列的最后一个元素,直接加入到子序列末尾
else:
# 使用二分查找找到当前元素在递增子序列中的位置,并替换对应位置的元素
left, right = 0, len(tails) - 1
while left < right:
mid = (left + right) // 2
if tails[mid] < num:
left = mid + 1
else:
right = mid
tails[left] = num
return len(tails) # 返回递增子序列的长度
674.最长连续递增序列
力扣链接
==动规五部曲 ==
- dp的定义
dp[i]表示子序列答案以nums[i]结尾的最长递增子序列的长度- 状态转移方程:
if nums[i] > nums[i-1]: dp[i] = dp[i-1]+1
- dp初始化
每一个i,对应的dp[i](即最长递增子序列)起始大小至少都是1- 确认遍历顺序:
class Solution:
def findLengthOfLCIS(self, nums: List[int]) -> int:
if len(nums) <= 1: return len(nums)
dp = [1] * len(nums) #dp[i]表示以nums[i]结尾的子序列的最长连续递增序列
res = 1
for i in range(1, len(nums)):
if nums[i] > nums[i-1]: #连续记录
dp[i] = dp[i-1]+1
else:
dp[i] = 1
res = max(res, dp[i])
return res
贪心
class Solution:
def findLengthOfLCIS(self, nums: List[int]) -> int:
if len(nums) == 0:
return 0
result = 1 #连续子序列最少也是1
count = 1
for i in range(len(nums)-1):
if nums[i+1] > nums[i]: #连续记录
count += 1
else: #不连续,count从头开始
count = 1
result = max(result, count)
return result
718.最长重复子数组【公共连续】
力扣链接

==动规五部曲 ==
- dp的定义
dp[i][j] :以下标i - 1为结尾的A,和以下标j - 1为结尾的B,最长重复子数组长度为dp[i][j]
(特别注意: 这个公共子字符串是下标i - 1为结尾的A )- 状态转移方程:
if nums1[i - 1] == nums2[j - 1]:
# 在当前位置上的最长公共子数组长度为前一个位置上的长度加一
dp[i][j] = dp[i - 1][j - 1] + 1
- dp初始化
dp[i][0] =dp[0][j]=0。- 确认遍历顺序:
class Solution:
def findLength(self, nums1: List[int], nums2: List[int]) -> int:
# 创建一个二维数组 dp,用于存储最长公共子数组的长度
dp = [[0] * (len(nums2) + 1) for _ in range(len(nums1) + 1)]
# 记录最长公共子数组的长度
result = 0
# 遍历数组 nums1
for i in range(1, len(nums1) + 1):
# 遍历数组 nums2
for j in range(1, len(nums2) + 1):
# 如果 nums1[i-1] 和 nums2[j-1] 相等
if nums1[i - 1] == nums2[j - 1]:
# 在当前位置上的最长公共子数组长度为前一个位置上的长度加一
dp[i][j] = dp[i - 1][j - 1] + 1
# 更新最长公共子数组的长度
res = max(res, dp[i][j])
# 返回最长公共子数组的长度
return result
1143.最长公共子序列【公共子序列】
力扣链接

==动规五部曲 ==
- dp的定义
dp[i][j]:长度为[0, i - 1]的字符串text1与长度为[0, j - 1]的字符串text2的最长公共子序列为dp[i][j]- 状态转移方程:
if (text1[i - 1] == text2[j - 1]) :
dp[i][j] = dp[i - 1][j - 1] + 1
else:
dp[i][j] = max(dp[i - 1][j], dp[i][j - 1])
- dp初始化
dp[i][0] =dp[0][j]=0。- 确认遍历顺序:
class Solution:
def longestCommonSubsequence(self, text1: str, text2: str) -> int:
# 创建一个二维数组 dp,用于存储最长公共子序列的长度
dp = [[0] * (len(text2) + 1) for _ in range(len(text1) + 1)]
# 遍历 text1 和 text2,填充 dp 数组
for i in range(1, len(text1) + 1):
for j in range(1, len(text2) + 1):
if text1[i - 1] == text2[j - 1]:
# 如果 text1[i-1] 和 text2[j-1] 相等,则当前位置的最长公共子序列长度为左上角位置的值加一
dp[i][j] = dp[i - 1][j - 1] + 1
else:
# 如果 text1[i-1] 和 text2[j-1] 不相等,则当前位置的最长公共子序列长度为上方或左方的较大值
dp[i][j] = max(dp[i - 1][j], dp[i][j - 1])
# 返回最长公共子序列的长度
return dp[len(text1)][len(text2)]
1035.不相交的线【公共子序列】
力扣链接

本题说是求绘制的最大连线数,其实就是求两个字符串的最长公共子序列的长度!
class Solution:
def maxUncrossedLines(self, A: List[int], B: List[int]) -> int:
dp = [[0] * (len(B)+1) for _ in range(len(A)+1)]
for i in range(1, len(A)+1):
for j in range(1, len(B)+1):
if A[i-1] == B[j-1]:
dp[i][j] = dp[i-1][j-1] + 1
else:
dp[i][j] = max(dp[i-1][j], dp[i][j-1])
return dp[-1][-1]
53.最大子序和
力扣链接

==动规五部曲 ==
- dp的定义
dp[i]:包括下标i(以nums[i]为结尾)的最大连续子序列和为dp[i]。- 状态转移方程:
for i in range(1, len(nums)):
dp[i] = max(dp[i-1] + nums[i], nums[i]) #状态转移公式
- dp初始化
dp[0] = nums[0]- 确认遍历顺序:
class Solution:
def maxSubArray(self, nums: List[int]) -> int:
dp = [0] * len(nums)
dp[0] = nums[0]
result = dp[0] # res的初始值是dp[0],不是0
for i in range(1, len(nums)):
dp[i] = max(dp[i-1] + nums[i], nums[i]) #状态转移公式
result = max(result, dp[i]) #result 保存dp[i]的最大值
return result
392.判断子序列【s在t是否出现】
力扣链接

==动规五部曲 ==
- dp的定义
dp[i][j]:以i-1为结尾的s子序列中出现以j-1为结尾的t的个数为dp[i][j]。- 状态转移方程:
if s[i-1] == t[j-1]:
dp[i][j] = dp[i-1][j-1] + 1
else:
dp[i][j] = dp[i][j-1]
- dp初始化
dp[0][0]和dp[i][0]为0- 确认遍历顺序:
class Solution:
def isSubsequence(self, s: str, t: str) -> bool:
dp = [[0] * (len(t)+1) for _ in range(len(s)+1)]
for i in range(1, len(s)+1):
for j in range(1, len(t)+1):
if s[i-1] == t[j-1]:
dp[i][j] = dp[i-1][j-1] + 1
else:
dp[i][j] = dp[i][j-1]
if dp[-1][-1] == len(s):
return True
return False
115.不同的子序列【s在t出现的个数】
力扣链接

==动规五部曲 ==
- dp的定义
dp[i][j]:以i-1为结尾的s子序列中,出现以j-1为结尾的t的个数为dp[i][j]。【s[0:i] 中,t[0:j]出现的个数】- 状态转移方程:
if s[i-1] == t[j-1]:
dp[i][j] = dp[i-1][j-1] + dp[i-1][j]
#1.用上了s[i-1] 2. 没有用上s[i-1],把s[i-1]删掉
else:
dp[i][j] = dp[i-1][j]
- dp初始化
dp[0][j]=0
dp[i][0]:以i-1为结尾的s可以随便删除元素,出现空字符串的个数。- 确认遍历顺序:
class Solution:
def numDistinct(self, s: str, t: str) -> int:
dp = [[0] * (len(t)+1) for _ in range(len(s)+1)]
for i in range(len(s)):
dp[i][0] = 1
for j in range(1, len(t)):
dp[0][j] = 0
for i in range(1, len(s)+1):
for j in range(1, len(t)+1):
if s[i-1] == t[j-1]:
dp[i][j] = dp[i-1][j-1] + dp[i-1][j]
else:
dp[i][j] = dp[i-1][j]
return dp[-1][-1]
583. 两个字符串的删除操作
力扣链接

==动规五部曲 ==
- dp的定义
dp[i][j]:以i-1为结尾的字符串word1,和以j-1位结尾的字符串word2,想要达到相等,所需要删除元素的最少次数。- 状态转移方程:
if word1[i-1] == word2[j-1]:
dp[i][j] = dp[i-1][j-1]
else:
dp[i][j] = min(dp[i-1][j-1] + 2, dp[i-1][j] + 1, dp[i][j-1] + 1)
- dp初始化
dp[0][j]=j
dp[i][0]=i- 确认遍历顺序:
class Solution:
def minDistance(self, word1: str, word2: str) -> int:
dp = [[0] * (len(word2)+1) for _ in range(len(word1)+1)]
for i in range(len(word1)+1):
dp[i][0] = i
for j in range(len(word2)+1):
dp[0][j] = j
for i in range(1, len(word1)+1):
for j in range(1, len(word2)+1):
if word1[i-1] == word2[j-1]:
dp[i][j] = dp[i-1][j-1]
else:
dp[i][j] = min(dp[i-1][j-1] + 2, dp[i-1][j] + 1, dp[i][j-1] + 1)
return dp[-1][-1]
class Solution(object):
def minDistance(self, word1, word2):
m, n = len(word1), len(word2)
# dp 求解两字符串最长公共子序列
dp = [[0] * (n+1) for _ in range(m+1)]
for i in range(1, m+1):
for j in range(1, n+1):
if word1[i-1] == word2[j-1]:
dp[i][j] = dp[i-1][j-1] + 1
else:
dp[i][j] = max(dp[i-1][j], dp[i][j-1])
# 删去最长公共子序列以外元素
return m + n - 2 * dp[-1][-1]
72.编辑距离
力扣链接

==动规五部曲 ==
- dp的定义
dp[i][j]:以i-1为结尾的字符串word1,和以j-1位结尾的字符串word2,想要达到相等,最小编辑距离为dp[i][j]。。- 状态转移方程:
if word1[i-1] == word2[j-1]:
dp[i][j] = dp[i-1][j-1]
else:
dp[i][j] = min(dp[i-1][j-1] + 1, dp[i-1][j] + 1, dp[i][j-1] + 1)
- dp初始化
dp[0][j]=j
dp[i][0]=i- 确认遍历顺序:
class Solution:
def minDistance(self, word1: str, word2: str) -> int:
dp = [[0] * (len(word2)+1) for _ in range(len(word1)+1)]
for i in range(len(word1)+1):
dp[i][0] = i
for j in range(len(word2)+1):
dp[0][j] = j
for i in range(1, len(word1)+1):
for j in range(1, len(word2)+1):
if word1[i-1] == word2[j-1]:
dp[i][j] = dp[i-1][j-1]
else:
dp[i][j] = min(dp[i-1][j-1] + 1, dp[i-1][j] + 1, dp[i][j-1] + 1)
return dp[-1][-1]
编辑距离总结篇
给定字符串 s 和 t ,判断 s 是否为 t 的子序列。
if (s[i - 1] == t[j - 1])
dp[i][j] = dp[i - 1][j - 1] + 1
else:
dp[i][j] = dp[i][j - 1] #相当于t要删除元素,继续匹配
给定一个字符串 s 和一个字符串 t ,计算在 s 的子序列中 t 出现的个数。
if (s[i - 1] == t[j - 1])
dp[i][j] = dp[i - 1][j - 1] + dp[i - 1][j]
#一部分是用s[i - 1]来匹配,那么个数为dp[i - 1][j - 1]。
#一部分是不用s[i - 1]来匹配,个数为dp[i - 1][j]。
else :
dp[i][j] = dp[i - 1][j];
给定两个单词 word1 和 word2,找到使得 word1 和 word2 相同所需的最少步数,每步可以删除任意一个字符串中的一个字符。
if (word1[i - 1] == word2[j - 1]) :
dp[i][j] = dp[i - 1][j - 1]
else :
dp[i][j] = min({dp[i - 1][j - 1] + 2, dp[i - 1][j] + 1, dp[i][j - 1] + 1})
给你两个单词 word1 和 word2,请你计算出将 word1 转换成 word2 所使用的最少操作数 。
if (word1[i - 1] == word2[j - 1]):
dp[i][j] = dp[i - 1][j - 1];
else:
dp[i][j] = min({dp[i - 1][j - 1], dp[i - 1][j], dp[i][j - 1]}) + 1