前言：简述单层感知机特征及三种表示方式，并用单层感知机描述门电路，借由单层感知机无法处理非线性空间的问题，引出多层感知机。

单层感知机

感知机（preceptron）接收多个输入信号，输出一个信号。

如下图所示为有两个输入的感知机。其中，$x_1$ 和 $x_2$ 为输入信号，$y$ 为输出信号，$w_1、w_2$ 为权重，输入信号分别乘上各自权重，若两者总和超过某一阈值 $\theta$，则输出1，类似于神经元被激活。

数学表示：
$$y=\{\begin{array}{l}0,w_1{x}_1+w_2{x}_2⩽\theta \\ 1,w_1{x}_1+w_2{x}_2>\theta \end{array}$$
权重 $w$ 表示信号的重要程度；阈值 $\theta$ 表示神经元被激活的难易程度，若 $\theta$ 为 -50，则神经元被激活难度大，反之难度小。

另一种数学表示：
$$y=\{\begin{array}{l}0,w_1{x}_1+w_2{x}_2+b⩽0\\ 1,w_1{x}_1+w_2{x}_2+b>0\end{array}$$
较上式，令 $b=-\theta$，称为偏执。这种表示方法便于编程时借助矩阵运算。

几何表示：表示空间中的一条直线，无法表示曲线。由直线划分的空间称为线性空间，由曲线划分的空间表示非线性空间。

---

感知机 与 门电路

感知机能够表示与门、或门、非门。

与门

与门（AND gate）是有两个输入和一个输出的门电路，与门特点是全1则1，其余为0。下表为与门真值表，即输入和输出信号的对应表。

$x_1$	$x_2$	$y$
0	0	0
0	1	0
1	0	0
1	1	1

数学表示：
$$y=\{\begin{array}{l}0,0.5x_1+0.5x_2⩽0.7\\ 1,0.5x_1+0.5x_2>0.7\end{array}$$
几何表示：

Python 实现：

#数学表示1
def AND_gate(x1, x2):
    w1, w2, theta = 0.5, 0.5, 0.7
    tmp = w1*x1 + w2*x2
    if tmp <= theta:
        return 0
    elif tmp > theta:
        return 1
    
# ===========================
# 数学表示2
import numpy as np
def AND_gate_1(x1, x2):
    x = np.array([x1, x2, 1])
    w = np.array([0.5, 0.5, -0.7])
    tmp = np.sum(w*x)
    if tmp <= 0:
        return 0
    elif tmp > 0:
        return 1

与非门

和「与门」的输出相反。
$$y=\{\begin{array}{l}0,-0.5x_1-0.5x_2⩽-0.7\\ 1,-0.5x_1-0.5x_2>-0.7\end{array}$$
Python实现：

import numpy as np
def NAND_gate(x1, x2):
    x = np.array([x1, x2, 1])
    w = np.array([-0.5, -0.5, 0.7])
    tmp = np.sum(w*x)
    if tmp <= 0:
        return 0
    elif tmp > 0:
        return 1

或门

有1则1，全0则0。
$$y=\{\begin{array}{l}0,0.5x_1+0.5x_2⩽0.2\\ 1,0.5x_1+0.5x_2>0.2\end{array}$$
Python 实现：

import numpy as np
def OR_gate(x1, x2):
    x = np.array([x1, x2, 1])
    w = np.array([0.5, 0.5, -0.2])
    tmp = np.sum(w*x)
    if tmp <= 0:
        return 0
    elif tmp > 0:
        return 1

异或门

仅当 $x_1、x_2$ 中一方为1时，才会输出 1。

$x_1$	$x_2$	$y$
0	0	0
0	1	1
1	0	1
1	1	0

无法用一条直线划分两种标记，因为感知机不能表示空间曲线。

多层感知机

单层感知机无法表示非线性空间，但多层感知机（multi-layered perceptron）可以表示。

通过叠加与、非与、或门实现异或门，Python 实现如下：

def XOR(x1, x2):
    s1 = NAND_gate(x1, x2)
    s2 = OR_gate(x1, x2)
    y = AND_gate(s1, s2)
    return y

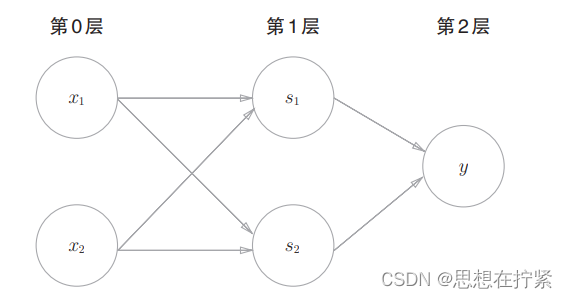
如下图所示为2层感知机，感知机总共由 3 层构成，但是因为拥有权重的层实质上只有 2 层（第 0 层和第 1 层之间，第 1 层和第 2 层之间），所以称为「2层感知机」。不过，若从 3 层结构来看，也可称为「3层感知机」。

---

参考书籍：
深度学习入门：基于Python的理论与实现 (斋藤康毅)