1.只出现一次的数字

我们可以使用异或运算来解决这个问题:
异或运算有一个重要的性质:两个相同的数进行异或运算结果为 0,任何数与 0 异或结果为其本身。对于数组中的元素,依次进行异或运算,出现两次的元素异或后会变成 0,最后剩下的就是只出现一次的那个元素。
以下是具体步骤:
数组 [2,2,1],2^2=0,0^1=1,所以输出 1。
那么请看正确代码:
class Solution {
public:
int singleNumber(vector<int>& nums) {
int val=0;
for(auto e :nums)
val^=e;
return val;
}
};这是一种方法,然而还有一种传统的方法:
class Solution {
public:
int singleNumber(vector<int>& nums) {
int flag=0;
for(size_t i=0;i<nums.size();i++)
{
flag=0;
for(size_t j=0;j<nums.size();j++)
{
if(nums[i]==nums[j]&&i!=j)
flag=1;
}
if(flag==0)
return nums[i];
}
return 0;
}
};上述代码首先创建一个变量flag并将其初始化为0,用于标记是否找到了只出现一次的元素。然后使用两个嵌套的循环遍历数组。外层循环用于遍历每个元素,内层循环用于比较当前元素与其他元素是否相等。如果找到了一个与当前元素相等且索引不同的元素,说明当前元素不是只出现一次的元素,将flag标记为1。最后,在外层循环中判断flag的值,如果flag为0,则说明当前元素是只出现一次的元素,直接返回该元素。如果循环结束后都没有找到只出现一次的元素,则返回0。
2.杨辉三角
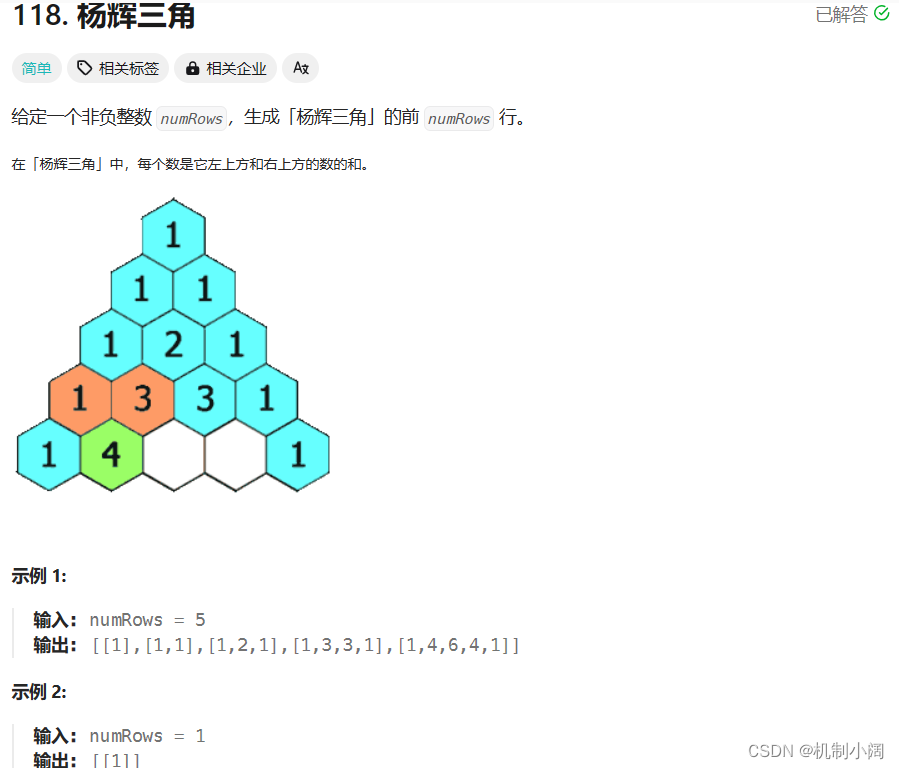
杨辉三角是一个数列,其第n行由 n个数字构成,每个数字等于它上方两个数字之和。首先,我们来看一下杨辉三角的定义:每一行的两侧数字都是1,中间的数字等于上一行对应位置的两个数字之和。可以使用二维数组来表示整个杨辉三角,其中第i行第j列的数字可以表示为triangle[i][j]。那么我们可以使用以下的编程思路来生成杨辉三角:
- 创建一个二维数组triangle,初始化为一个空的二维数组。
- 使用两个嵌套的循环来遍历杨辉三角的每一行和每一列,外层循环控制行数,内层循环控制列数。
- 在内层循环中,对于每一行的第一个位置和最后一个位置,将其值设置为1。
- 对于其他位置,将其值设置为其上一行对应位置的两个数字之和,即triangle[i][j] = triangle[i-1][j-1] + triangle[i-1][j]。
- 内层循环结束后,将当前行的数组添加到triangle中。
- 外层循环结束后,triangle中存储的就是完整的杨辉三角
请看正确代码:
class Solution {
public:
vector<vector<int>> generate(int numRows) {
vector<vector<int>> triangle;
if (numRows <= 0) {
return triangle;
}
for (int i = 0; i < numRows; i++) {
vector<int> row(i+1, 1); // 初始化每一行为1
for (int j = 1; j < i; j++) {
row[j] = triangle[i-1][j-1] + triangle[i-1][j]; // 计算其他位置的值
}
triangle.push_back(row); // 将当前行添加到triangle中
}
return triangle;
}
};这段代码使用了一个二维数组triangle来存储杨辉三角的每一行的数字。首先判断numRows的值,如果小于等于0,则直接返回空的triangle。然后,使用两个嵌套的循环来遍历杨辉三角的每一行和每一列。外层循环控制行数,内层循环控制列数。在内层循环中,对于每一行的第一个位置和最后一个位置,将其值设置为1。对于其他位置,将其值设置为其上一行对应位置的两个数字之和。内层循环结束后,将当前行的数组添加到triangle中。最后返回triangle即可得到完整的杨辉三角。这段代码的时间复杂度为O(numRows^2),其中numRows为所要生成杨辉三角的行数。因为需要使用两个嵌套的循环来遍历杨辉三角的每一行和每一列,时间复杂度较高。
3.删除有序数组中的重复项

删除有序数组中的重复项可以使用双指针的方法来实现。具体的编程思路如下:
- 初始化两个指针:一个指针i用于遍历整个数组,另一个指针j用于指向当前确定的不重复元素的位置。
- 从数组的第二个元素开始遍历,即i=1。
- 如果当前元素nums[i]与前一个元素nums[i-1]相等,表示出现了重复元素,此时指针i继续向后移动一位。
- 如果当前元素nums[i]与前一个元素nums[i-1]不相等,表示找到了一个不重复的元素,将其复制到指针j的位置,并将指针j向后移动一位。
- 重复步骤3和步骤4,直到遍历完整个数组。
- 返回指针j的位置+1,即为删除重复项后的数组长度。
class Solution {
public:
int removeDuplicates(vector<int>& nums) {
if (nums.size() == 0) {
return 0;
}
int j = 1; // 指针j初始指向第一个不重复元素的位置
for (int i = 1; i < nums.size(); i++) {
if (nums[i] != nums[i-1]) {
nums[j++] = nums[i]; // 复制非重复元素到指针j的位置
}
}
return j;
}
};
这段代码使用了两个指针i和j。指针i用于遍历整个数组,指针j用于指向当前确定的不重复元素的位置。首先判断数组的长度是否为0,如果是则直接返回0。然后从数组的第二个元素开始遍历,即i=1。如果当前元素nums[i]与前一个元素nums[i-1]相等,表示出现了重复元素,此时指针i继续向后移动一位。如果当前元素nums[i]与前一个元素nums[i-1]不相等,表示找到了一个不重复的元素,将其复制到指针j的位置,并将指针j向后移动一位。重复上述步骤直到遍历完整个数组,最后返回指针j的位置+1,即为删除重复项后的数组长度。这段代码的时间复杂度为O(n),其中n为数组的长度。只需要遍历一次数组即可删除重复项,时间复杂度较低。
4.只出现一次的数字2.0

这道题和第一道题思路大概一致,只不过这里的重复次数变成了3次,还能不能使用异或呢,显然不能了,那我们第一道题的第二种方法能不能解呢?答案是可以的,那么请看示例代码:
class Solution {
public:
int singleNumber(vector<int>& nums) {
int flag=0;
for(size_t i=0;i<nums.size();i++)
{
flag=0;
for(size_t j=0;j<nums.size();j++)
{
if(nums[i]==nums[j]&&i!=j)
flag=1;
}
if(flag==0)
return nums[i];
}
return 0;
}
};这里就不在解析了,思路和第一题的第二种方法一样。
5.只出现一次的数字3.0

思路依旧类似,只不过需要返回多个元素,只需要尾插到顺序表中即可,请看示例代码:
class Solution {
public:
vector<int> singleNumber(vector<int>& nums) {
vector<int> vv;
int flag=0;
for(size_t i=0;i<nums.size();i++)
{
flag=0;
for(size_t j=0;j<nums.size();j++)
{
if(nums[i]==nums[j]&&i!=j)
flag=1;
}
if(flag==0)
vv.push_back(nums[i]);
}
return vv;
}
};写法和前两种基本相似,不同之处在于,找到之后不会直接返回,而是尾插到顺序表中最后一块返回。
6.数组中出现次数超过一半的数字

常规写法就是统计他们出现的总次数,然后进行判断是否大于数组长度的一半,请看示例代码:
int count=0;
for(size_t i=0;i<numbers.size();i++)
{
count=1;
for(size_t j=0;j<numbers.size();j++)
{
if(numbers[i]==numbers[j]&&i!=j)
count++;
}
if(count>numbers.size()/2)
return numbers[i];
}
return 0;上述代码的具体的分析如下:
1. 初始化计数变量`count`为0。
2. 使用嵌套的循环结构遍历数组元素,外层循环是遍历数组中的每一个元素,内层循环是用来统计数组中该元素出现的次数。
3. 对于每一个外层循环迭代的元素,首先将计数变量`count`重置为1,表示当前元素至少出现了一次。
4. 然后通过内层循环遍历数组中的每一个元素,如果发现数组中有与当前元素相等的元素且索引不同,就将计数变量`count`加1。
5. 在内层循环结束后,判断计数变量`count`是否超过了数组长度的一半,如果超过了则说明该元素出现次数超过了数组长度的一半,直接返回该元素。
6. 如果没有找到出现次数超过数组长度一半的元素,最后返回0。
这段代码的时间复杂度为O(n^2),其中n为数组的长度。因为嵌套循环的复杂度为O(n^2),每个元素都需要遍历一次数组进行统计。所以在数组较大时,性能可能比较差。
那么有没有什么简单的方法呢?
分析一下题中的关键字“数组长度的一半“能不能想到把这个数组排序一下中间的就是我们要找的呢?哈哈,巧妙吧?那么请看示例代码吧:
class Solution {
public:
int MoreThanHalfNum_Solution(vector<int>& numbers) {
sort(numbers.begin(),numbers.end());
return numbers[numbers.size()/2];
}
};直接对数组进行排序,取其中间值就行。
到此我们只是简单的讲解了一下STL中vector的相关习题~,后续我们会一一展开学习的,希望这篇博客能给您带来一些启发和思考!那我们下次再一起探险喽,欢迎在评论区进行讨论~~~











![【例子】webpack配合babel实现 es6 语法转 es5 案例 [通俗易懂]](https://img-blog.csdnimg.cn/direct/60f0f5c8ae274c05ac49ea480c76c872.png)