二分练习题（C. Earning on Bets）

原题链接：点击此处

Earning on Bets

题面翻译

有人提议让您玩一个游戏。在这个游戏中，有 $n$ 种可能的结果，对于每一种结果，您都必须下注一定整数的硬币。如果 $i$ 的结果是赢，您将获得与您在该结果上的投注额相等的硬币，再乘以 $k_i$。请注意， $n$ 个结果中有且只有一个结果是赢的。

你的任务是决定如何分配硬币，以便在出现任何获胜结果时都能获胜。更正式地说，你对所有结果下注的硬币总数必须严格地小于每个可能获胜的结果所得到的硬币数量。

题目描述

You have been offered to play a game. In this game, there are $ n $ possible outcomes, and for each of them, you must bet a certain integer amount of coins. In the event that the $ i $ -th outcome turns out to be winning, you will receive back the amount of coins equal to your bet on that outcome, multiplied by $ k_i $ . Note that exactly one of the $ n $ outcomes will be winning.

Your task is to determine how to distribute the coins in such a way that you will come out ahead in the event of any winning outcome. More formally, the total amount of coins you bet on all outcomes must be strictly less than the number of coins received back for each possible winning outcome.

输入格式

Each test consists of multiple test cases. The first line contains a single integer $ t $ ( $ 1 \le t \le 10^4 $ ) — the number of test cases. The description of the test cases follows.

The first line of each test case contains a single integer $ n $ ( $ 1 \le n \le 50 $ ) — the number of outcomes.

The second line of each test case contains $ n $ integers $ k_1,k_2,\ldots,k_n $ ( $ 2 \le k_i \le 20 $ ) — the multiplier for the amount of coins if the $ i $ -th outcome turns out to be winning.

It is guaranteed that the sum of $ n $ over all test cases does not exceed $ 2 \cdot 10^5 $ .

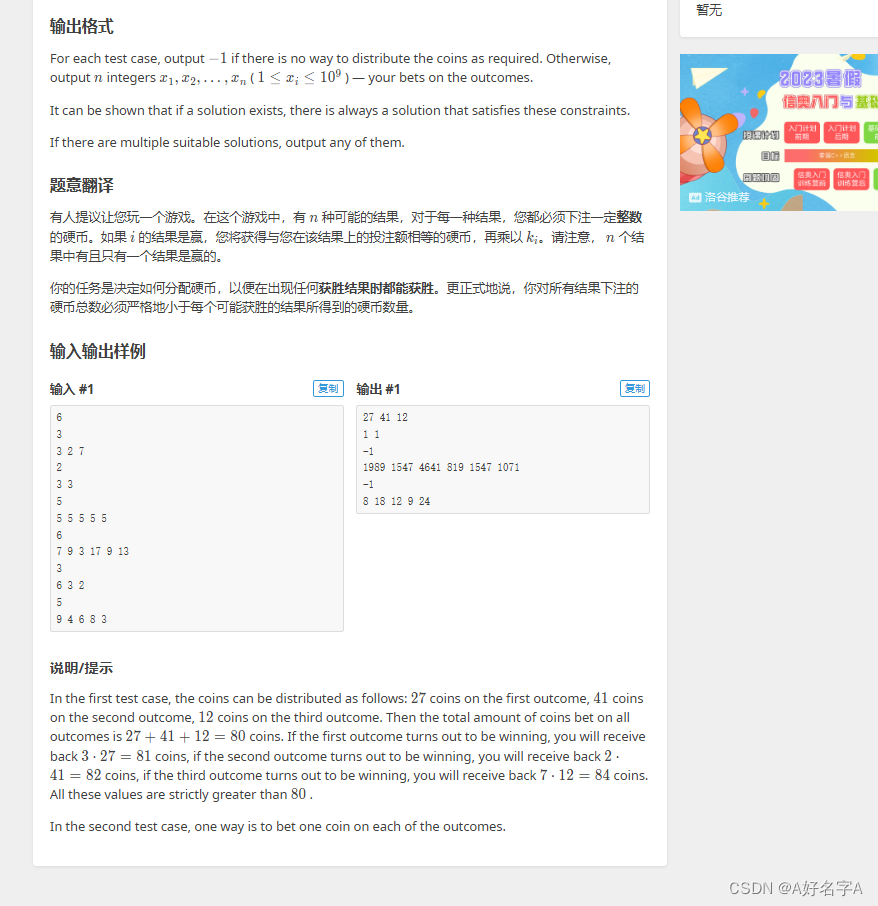
输出格式

For each test case, output $ -1 $ if there is no way to distribute the coins as required. Otherwise, output $ n $ integers $ x_1, x_2,\ldots, x_n $ ( $ 1 \le x_i \le 10^{9} $ ) — your bets on the outcomes.

It can be shown that if a solution exists, there is always a solution that satisfies these constraints.

If there are multiple suitable solutions, output any of them.

样例 #1

样例输入 #1

6
3
3 2 7
2
3 3
5
5 5 5 5 5
6
7 9 3 17 9 13
3
6 3 2
5
9 4 6 8 3

样例输出 #1

27 41 12 
1 1 
-1
1989 1547 4641 819 1547 1071 
-1
8 18 12 9 24

提示

In the first test case, the coins can be distributed as follows: $ 27 $ coins on the first outcome, $ 41 $ coins on the second outcome, $ 12 $ coins on the third outcome. Then the total amount of coins bet on all outcomes is $ 27 + 41 + 12 = 80 $ coins. If the first outcome turns out to be winning, you will receive back $ 3 \cdot 27 = 81 $ coins, if the second outcome turns out to be winning, you will receive back $ 2 \cdot 41 = 82 $ coins, if the third outcome turns out to be winning, you will receive back $ 7 \cdot 12 = 84 $ coins. All these values are strictly greater than $ 80 $ .

In the second test case, one way is to bet one coin on each of the outcomes.

题目意思

 给出一个序列k，让你自己再构造出来一个序列a，序列a的总和s，确保$k_i\ast a_i>=s$。答案可能有很多个，只需输出一个即可。数据范围可以参考上文的范围。

思路

 个人感觉，这一题的难度就在于如何找到序列a的总和s，总和s一旦找出来，问题就很轻松的解决了，一开始将数据范围看错了，误以为总和s最大为$2e5$了，就将s当成200000来算，结果一直过不去，后来才发不止那么简单。重新思考一下，我们可以利用二分的思想，我们可以二分出来一个最小的s值且这个s的值符合序列a的要求。问题在于我们如何将s二分出来呢？
我们可以发现$k_i\ast a_i>=s$，转换一下$a_i>=s/k_i+1$，利用这个思想我们就可以写出来check函数里面的内容了。

//check函数内容如下
bool check (int x) {
	int sum=x;
	for (int i=1;i<=n;i++) {
		sum-=x/a[i];
	}
	return sum>=n;
}

 check函数一旦写出来，我们就找到了s的值，这样我们就可以进行代码实现操作了。将$a_i$的值赋值为$s/k_i+1$，每一个$a_i$都这样写，最后一个看情况而定，途中判断是否能赋值完成，如果完不成就输出-1

//利用map<PII,int>来存住大小和位置，以解决相同大小的情况
	int pos=l,pp=l;//定义两个变量，pos是总值一直不变，pp一直变换，如果途中小于0，就输出-1
	int k=0;int f=1;
	for (int i=1;i<=n;i++) {
		if (i==n) {
			int t=pos/a[i]+1;
			if (t<=pp)
			mp[{a[i],i}]=pp;
			else f=0;
			continue;
		}//特判最后一个
		mp[{a[i],i}]=(pos/a[i])+1;
		pp-=mp[{a[i],i}];
		if (pp<=0) {
			f=0;
		}
	}
	if (f==0) {
		cout<<"-1"<<'\n';
	}
	else {
		for (int i=1;i<=n;i++) {
			cout<<mp[{a[i],i}]<<' ';//输出即可
		}
		cout<<'\n';
	}

 下面附上AC代码(仅供参考)

#include<bits/stdc++.h>
#define int long long 
#define endl "\n"
#define fi first
#define se second
#define PII pair<int,int> 
#define lowbit(x) (x&(-x))
#define ALL(x) x.begin(),x.end() 
using namespace std;
const int N=1e6+5;
int a[N],b[N];
int n;
bool check (int x) {
	int sum=x;
	for (int i=1;i<=n;i++) {
		sum-=x/a[i];
	}
	return sum>=n;
}

void solve()
{
	cin>>n;
	map<PII,int>mp;
	for (int i=1;i<=n;i++) {
		cin>>a[i];
	}
	
	int l=n-1,r=n*(int)1e9+1;
	while (l<r) {
		int mid=l+r>>1;
		if (check(mid)) r=mid;
		else l=mid+1;
	}
	int pos=l,pp=l;
	int k=0;int f=1;
	for (int i=1;i<=n;i++) {
		if (i==n) {
			int t=pos/a[i]+1;
			if (t<=pp)
			mp[{a[i],i}]=pp;
			else f=0;
			continue;
		}
		mp[{a[i],i}]=(pos/a[i])+1;
		pp-=mp[{a[i],i}];
		if (pp<=0) {
			f=0;
		}
	}
	if (f==0) {
		cout<<"-1"<<'\n';
	}
	else {
		for (int i=1;i<=n;i++) {
			cout<<mp[{a[i],i}]<<' ';
		}
		cout<<'\n';
	}
	return ;
}
signed main()
{
	ios::sync_with_stdio(0);cin.tie(0);cout.tie(0);
	int T=1;
	cin >> T;
	while(T--) solve();
	return 0;
}