【因果推断python】45

问题设置

目标转换

到目前为止，我们已经了解了如何在干预不是随机分配的情况下对我们的数据进行纠偏，这会导致混淆偏差。这有助于我们解决因果推理中的识别问题。换句话说，一旦单位是可交换的，或者 $Y(0),Y(1)\perp X$ ，就可以学习干预效果。但我们还远远没有完成。

识别意味着我们可以找到平均的干预效果。换句话说，我们知道一种干预的平均效果。当然，这很有用，因为它可以帮助我们决定是否应该真正实施干预。但我们想要的不止这些。我们想知道是否存在对干预反应更好或更差的单位亚组。这应该允许一个更好的策略，我们只对那些将从中受益的人进行干预。

问题设置

让我们回顾一下我们感兴趣的设置。鉴于潜在结果，我们可以将个体颗粒度的干预效果定义为潜在结果之间的差异。

$\tau_i=Y_i(1)-Y_i(0)$ ,

或者，连续处理情况， $\tau_i=\partial Y(t)$ ，其中 t 是处理变量。当然，我们永远无法观察个体的干预效果，因为我们只能看到潜在的结果之一

我们可以将平均干预效果 (ATE) 定义为

$\tau=E[Y_i(1)-Y_i(0)]=E[\tau_i]$

和条件平均干预效果（CATE）为

$\tau(x)=E[Y_i(1)-Y_i(0)|X]=E[\tau_i|X]$

在第一部分，我们主要关注 ATE。现在，我们对 CATE 很感兴趣。 CATE 对于个性化决策过程很有用。例如，如果您有一种药物作为干预方法 t，您想知道哪种类型的患者对药物的反应更高（更高的 CATE），以及是否有某些类型的患者有负面反应（类别 < 0)。

我们已经了解了如何使用线性回归以及干预和特征之间的交互来估计 CATE

$y_i=\beta_0+\beta_1t_i+\beta_2X_i+\beta_3t_iX_i+e_i$

如果我们估计这个模型，我们可以得到 $\tau(x)$ 的估计值

$\hat{\tau}(x)=\hat{\beta}_1+\hat{\beta}_3t_iX_i$

尽管如此，线性模型仍有一些缺点。主要的一个是对 X 的线性假设。请注意，您甚至不关心此模型上的 $\beta_{2}$ 。但是，如果特征 X 与结果没有线性关系，则您对因果参数 $\beta_{1}$ 和 $\beta_{3}$ 的估计将不正确。

如果我们可以用更灵活的机器学习模型代替线性模型，那就太好了。我们甚至可以将处理作为特征插入 ML 模型，例如提升树（boosted tree）或神经网络

$y_i=M(X_i,T_i)+e_i$

但我们如何从模型获得干预效果的估计值还不清楚，因为这个模型将输出 $\hat{y}$ 预测，而不是 $\tau\hat{(x)}$ 预测。理想情况下，我们将使用机器学习回归模型，而不是最小化结果 MSE

$E[(Y_i-\hat{Y}_i)^2]$

将最小化干预效果 MSE

$E[(\tau(x)_i-\hat{\tau}(x)_i)^2]=E[(Y_i(1)-Y_i(0)-\hat{\tau}(x)_i)^2]$

但是，这个标准就是我们所说的不可行。同样，这里的问题是 $\tau(x)_i$ 是不可观察的，所以我们不能直接优化它。这让我们陷入了困境……让我们试着把它简化一下，也许我们可以想到一些事情。

目标转换

假设您的干预是二元的。假设您是一家投资公司，正在测试发送金融教育电子邮件的有效性。你希望这封电子邮件能让人们进行更多投资。另外，假设您进行了一项随机研究，其中 50% 的客户收到了电子邮件，而另外 50% 的客户没有收到。

这是一个疯狂的想法：让我们通过将结果变量与干预相乘来转换结果变量。

$Y_i^*=2Y_i*T_i-2Y_i*(1-T_i)$

因此，如果单位被处理，您将取结果并将其乘以 2。如果未处理，您将取结果并将其乘以 -2。例如，如果您的一位客户投资了 2000,00 巴西雷亚尔并收到了电子邮件，则转换后的目标将为 4000。但是，如果他或她没有收到电子邮件，则为 -4000。

这似乎很奇怪，因为您说电子邮件的效果可以是负数，但对我来说是无用的。如果我们做一些数学运算，我们可以看到，平均或预期，这个转换后的目标将是干预效果。这简直太不可思议了。我要说的是，通过应用这种有点古怪的转换，我可以估计一些我什至无法观察到的东西。

要理解这一点，我们需要一些数学知识。由于随机分配，我们有 $T\perp Y(1),Y(1)$ ，这是我们的老朋友。这意味着 $E[T,Y(t)]=E[T]*E[Y(t)]$ ，这是独立性的定义。

另外，我们知道

$Y_i*T_i=Y_(1)i*T_i , Y_i*(1-T_i)=Y_(0)i*T_i$

因为干预是实现一种或其他潜在结果的原因。考虑到这一点，让我们取 $Y_i^*$ 的期望值，看看我们最终会得到什么。

因此，这个看似疯狂的想法最终成为了对个体干预效果的无偏估计 $\tau(x)_i$ 。现在，我们可以将不可行的优化标准替换为

$E[(Y_i^*-\hat{\tau}(x)_i)^2]$

简单来说，我们所要做的就是使用任何回归机器学习模型来预测 $Y_i^*$ 并且该模型将输出干预效果预测。

既然我们已经解决了简单的情况，那么更复杂的情况呢，干预不是 50% 50%，甚至不是随机分配的呢？事实证明，答案有点复杂，但并不多。首先，如果我们没有随机分配，我们至少需要条件独立 $T\perp Y(1),Y(1)|X$ 。也就是说，控制 X, T 与随机一样好。这样，我们可以将转换后的目标泛化为

$Y_i^*=Y_i*\frac{T_i-e(X_i)}{e(X_i)(1-e(X_i))}$

其中 $e(X_i)$ 是倾向得分。因此，如果干预不是 50% 50%，而是以不同的概率 p 随机化，您所要做的就是将上述公式中的倾向得分替换为 p。如果干预不是随机的，那么您必须使用存储或估计的倾向得分。

如果您对此进行预期，您会发现它也与干预效果相匹配。证明留给读者作为练习。开个玩笑，就在这里。这有点麻烦，所以请随意跳过它。

与往常一样，我认为这将通过一个示例变得更加具体。同样，考虑一下我们发送的试图让人们进行更多投资的投资电子邮件。结果变量二进制（投资与未投资）“转换”。

import pandas as pd
import numpy as np
from matplotlib import pyplot as plt
import seaborn as sns
from nb21 import cumulative_gain, elast
email = pd.read_csv("./data/invest_email_rnd.csv")
email.head()

我们的目标是个性化之一。让我们关注 email-1。我们希望仅将其发送给那些对其反应更好的客户。换句话说，我们希望估计 email-1 的条件平均处理效果

$E[Converted(1)_i-Converted(0)_i|X_i=x]=\tau(x)_i$

这样我们就可以定位那些对电子邮件反应最好的客户（更高的 CATE）

但首先，让我们将数据集分解为训练集和验证集。我们将在一组上估计 $\tau(x)_i$ 并评估另一组的估计。

from sklearn.model_selection import train_test_split

np.random.seed(123)
train, test = train_test_split(email, test_size=0.4)
print(train.shape, test.shape)
(9000, 8) (6000, 8)

现在，我们将应用我们刚刚学习的目标转换。由于电子邮件是随机分配的（尽管不是在 50% 50% 的基础上），我们不需要担心倾向得分。相反，它是恒定的并且等于干预概率。

y = "converted"
T = "em1"
X = ["age", "income", "insurance", "invested"]

ps = train[T].mean()

y_star_train = train[y] * (train[T] - ps)/(ps*(1-ps))

使用转换后的目标，我们可以选择任何 ML 回归算法来预测它。让我们在这里使用提升树（boosted tree）。

from lightgbm import LGBMRegressor

np.random.seed(123)
cate_learner = LGBMRegressor(max_depth=3, min_child_samples=300, num_leaves=5)
cate_learner.fit(train[X], y_star_train);

该模型现在可以估计 �(�)�。换句话说，它输出的是 �^(�)�。例如，如果我们对测试集进行预测，我们会看到某些单元的 CATE 比其他单元高。例如，客户 6958 的 CATE 为 0.1，这意味着如果我们向该客户发送电子邮件，他或她购买我们的投资产品的概率预计会增加 0.1。相反，对于客户 3903，预计购买该产品的概率仅增加 0.04。

test_pred = test.assign(cate=cate_learner.predict(test[X]))
test_pred.head()

为了评估这个模型有多好，我们可以展示训练集和测试集的累积增益曲线。

gain_curve_test = cumulative_gain(test_pred, "cate", y="converted", t="em1")
gain_curve_train = cumulative_gain(train.assign(cate=cate_learner.predict(train[X])), "cate", y="converted", t="em1")
plt.plot(gain_curve_test, color="C0", label="Test")
plt.plot(gain_curve_train, color="C1", label="Train")
plt.plot([0, 100], [0, elast(test, "converted", "em1")], linestyle="--", color="black", label="Baseline")
plt.legend();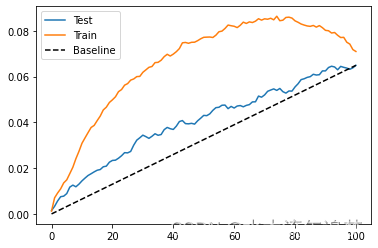

正如我们所看到的，这个即插即用的估计器在测试集上比随机的要好。尽管如此，它看起来还是过拟合了很多，因为在训练集上的表现比在测试集上的表现要好得多。

这实际上是这种目标转换技术的最大缺点之一。使用此目标转换，您确实获得了很多简单性，因为您只需转换目标并使用任何 ML 估计器来预测异构干预效果。它的代价是你会得到很多差异。这是因为转换后的目标是对个体干预效果的非常嘈杂的估计，并且该方差会转移到您的估计中。如果您没有大量数据，这将是一个大问题，但在处理超过 1MM 样本的大数据应用程序中应该问题不大。